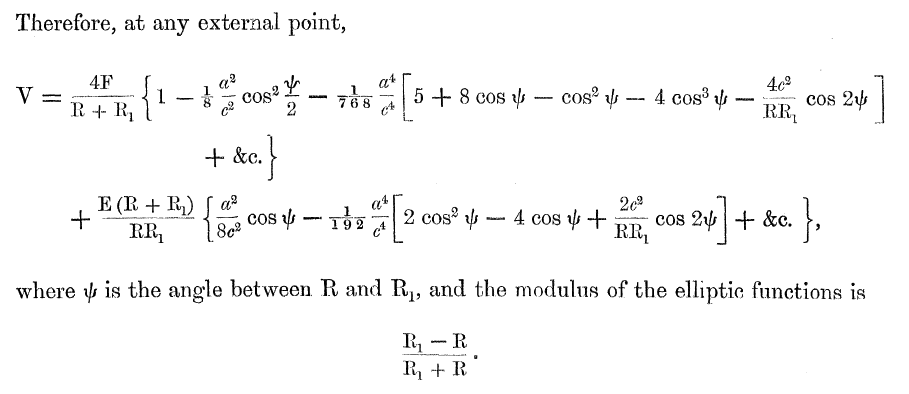Difference between revisions of "User:Tohline/Apps/DysonPotential"

From VistrailsWiki
Jump to navigation Jump to search
Line 27: Line 27:
</tr>
</tr>
</table>
</table>
In Dyson's expression, the leading factor of <math>~F</math> is the [https://en.wikipedia.org/wiki/Elliptic_integral#Complete_elliptic_integral_of_the_first_kind complete elliptic integral of the first kind], namely,
<table border="0" cellpadding="5" align="center">
<tr>
  <td align="right">
<math>~F = F(\mu)</math>
  </td>
  <td align="center">
<math>~\equiv</math>
  </td>
  <td align="left">
<math>~\int_0^{\pi/2} \frac{d\phi}{\sqrt{1 - \mu^2 \sin^2\phi}} \, ,</math>
  </td>
</tr>
</table>
where, <math>~\mu \equiv (R_1 - R)/(R_1 + R)</math>.  Similarly, <math>~E = E(\mu)</math> is the [https://en.wikipedia.org/wiki/Elliptic_integral#Complete_elliptic_integral_of_the_second_kind complete elliptic integral of the second kind].  In the limit of <math>~a/c \rightarrow 0</math>, Dyson's expression gives,
<table border="0" cellpadding="5" align="center">
<tr>
  <td align="right">
<math>~V_\mathrm{Dyson}</math>
  </td>
  <td align="center">
<math>~=</math>
  </td>
  <td align="left">
<math>~\frac{K(\mu)}{R_1+R_2} \, ,</math>
  </td>
</tr>
</table>
where we have acknowledged that, in the twenty-first century, the complete elliptic integral of the first kind is more customarily represented by the letter, <math>~K</math>. 


<table border="0" cellpadding="8" align="center"><tr><td align="center">
<table border="0" cellpadding="8" align="center"><tr><td align="center">

Revision as of 21:58, 26 August 2018

Dyson (1893)

Whitworth's (1981) Isothermal Free-Energy Surface
|   Tiled Menu   |   Tables of Content   |  Banner Video   |  Tohline Home Page   |

Overview

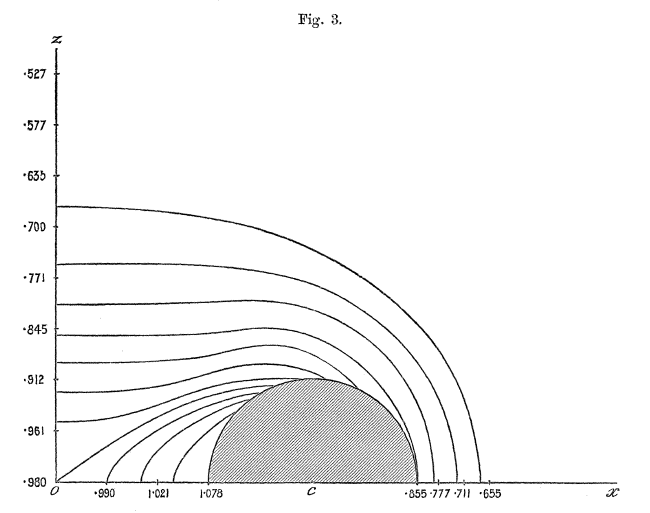
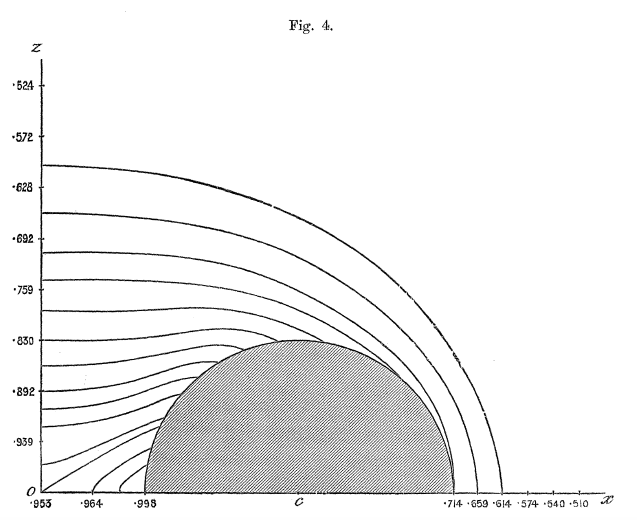
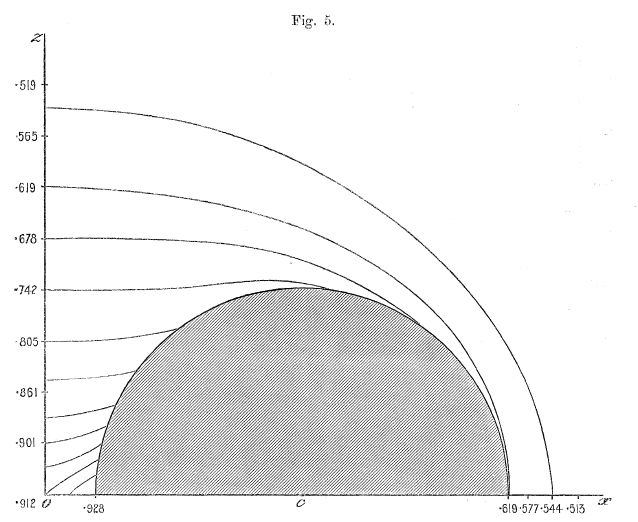
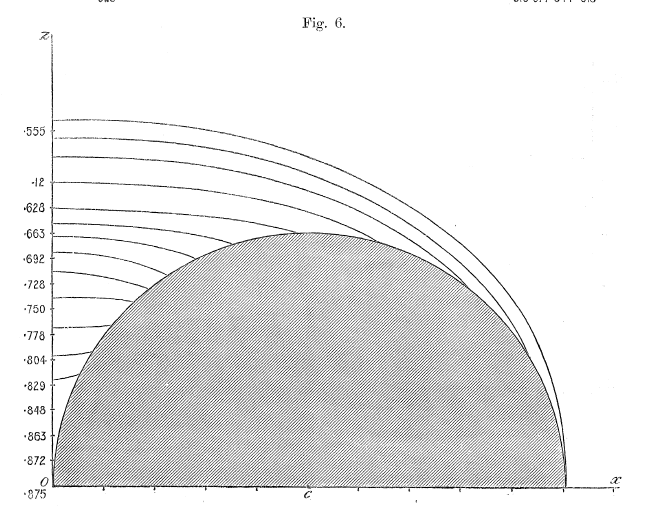
In his pioneering work, F. W. Dyson (1893, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95) and (1893, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106) used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. C.-Y. Wong (1974, ApJ, 190, 675 - 694) extended Dyson's work, using numerical techniques to obtain more accurate — but still approximate — equilibrium structures for incompressible tori having solid body rotation. Since then, Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) and I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613) have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence.

External Potential

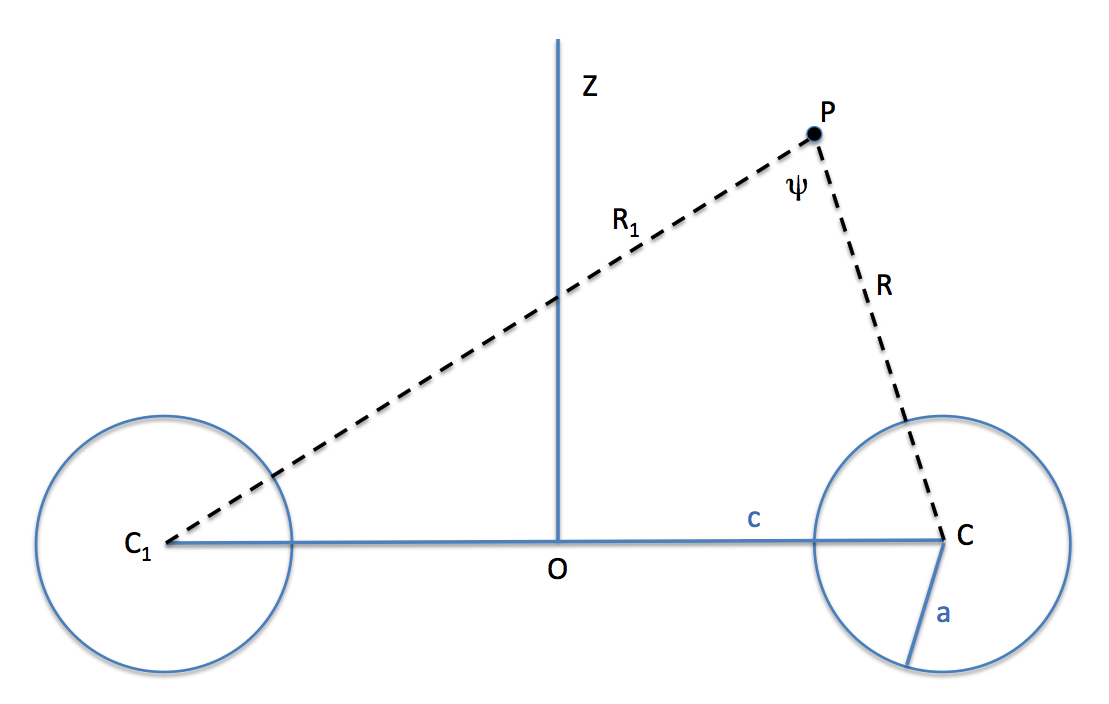
On p. 62 of F. W. Dyson (1893, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95), Dyson presents the following approximate expression for the potential everywhere exterior to an anchor ring:

Equation image extracted without modification from p. 62 of F. W. Dyson (1893)

The Potential of an Anchor Ring, Phil. Trans. Royal Soc. London. A., Vol. 184

The Potential Exterior to an Anchor Ring

Anchor ring schematic, adapted from figure near the top of §2 (on p. 47) of Dyson (1893a)

Anchor Ring Schematic

In Dyson's expression, the leading factor of <math>~F</math> is the complete elliptic integral of the first kind, namely,

<math>~F = F(\mu)</math>

<math>~\equiv</math>

<math>~\int_0^{\pi/2} \frac{d\phi}{\sqrt{1 - \mu^2 \sin^2\phi}} \, ,</math>

where, <math>~\mu \equiv (R_1 - R)/(R_1 + R)</math>. Similarly, <math>~E = E(\mu)</math> is the complete elliptic integral of the second kind. In the limit of <math>~a/c \rightarrow 0</math>, Dyson's expression gives,

<math>~V_\mathrm{Dyson}</math>

<math>~=</math>

<math>~\frac{K(\mu)}{R_1+R_2} \, ,</math>

where we have acknowledged that, in the twenty-first century, the complete elliptic integral of the first kind is more customarily represented by the letter, <math>~K</math>.

Figures 1 - 6 extracted without modification from pp. 63-66 of F. W. Dyson (1893)

The Potential of an Anchor Ring, Phil. Trans. Royal Soc. London. A., Vol. 184

The Potential Exterior to an Anchor Ring; R/d = infinity
The Potential Exterior to an Anchor Ring; R/d = 5
The Potential Exterior to an Anchor Ring; R/d = 2.5
The Potential Exterior to an Anchor Ring; R/d = 1.667
The Potential Exterior to an Anchor Ring; R/d = 1.25
The Potential Exterior to an Anchor Ring; R/d = 1

See Also

The following quotes have been taken from Petroff & Horatschek (2008):

§1:   "The problem of the self-gravitating ring captured the interest of such renowned scientists as Kowalewsky (1885), Poincaré (1885a,b,c) and Dyson (1892, 1893). Each of them tackled the problem of an axially symmetric, homogeneous ring in equilibrium by expanding it about the thin ring limit. In particular, Dyson provided a solution to fourth order in the parameter <math>~\sigma = a/b</math>, where <math>~a = r_t</math> provides a measure for the radius of the cross-section of the ring and <math>~b = \varpi_t</math> the distance of the cross-section's centre of mass from the axis of rotation."

§7:   "In their work on homogeneous rings, Poincaré and Kowalewsky, whose results disagreed to first order, both had made mistakes as Dyson has shown. His result to fourth order is also erroneous as we point out in Appendix B."

  1. Shortly after their equation (3.2), Marcus, Press & Teukolsky make the following statement: "… we know that an equilibrium incompressible configuration must rotate uniformly on cylinders (the famous "Poincaré-Wavre" theorem, cf. Tassoul 1977, &Sect;4.3) …"


 

Whitworth's (1981) Isothermal Free-Energy Surface

© 2014 - 2021 by Joel E. Tohline
|   H_Book Home   |   YouTube   |
Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS |
Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation

Retrieved from "https://www.vistrails.org//index.php?title=User:Tohline/Apps/DysonPotential&oldid=16279"