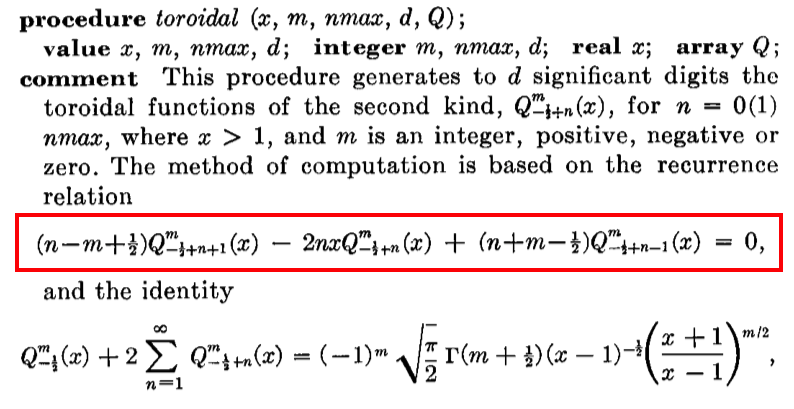Difference between revisions of "User:Tohline/Appendix/Mathematics/ToroidalFunctions"
| (45 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
==Wong Toroidal Coordinates== | ==Wong Toroidal Coordinates== | ||
===Wong's Expression for the Potential=== | |||
This chapter has been put together in an effort to lay the groundwork for an evaluation of [[User:Tohline/Apps/DysonWongTori#Wong_.281973.2C_1974.29|Wong's (1973)]] derived expression for the gravitational potential both inside and outside of a uniform-density, axisymmetric torus. After multiplying his expression by the negative of {{ User:Tohline/Math/C_GravitationalConstant }}, then replacing his total charge, <math>~q</math>, with the total mass, <math>~M</math>, Wong's ''interior'' (i.e., <math>~\eta^' > \eta_0</math>) solution is, | This chapter has been put together in an effort to lay the groundwork for an evaluation of [[User:Tohline/Apps/DysonWongTori#Wong_.281973.2C_1974.29|Wong's (1973)]] derived expression for the gravitational potential both inside and outside of a uniform-density, axisymmetric torus. After multiplying his expression by the negative of {{ User:Tohline/Math/C_GravitationalConstant }}, then replacing his total charge, <math>~q</math>, with the total mass, <math>~M</math>, Wong's ''interior'' (i.e., <math>~\eta^' > \eta_0</math>) solution is, | ||
| Line 76: | Line 78: | ||
</table> | </table> | ||
</div> | </div> | ||
===Summary of Toroidal Coordinates and Toroidal Functions=== | |||
<table border="1" cellpadding="8" width="85%" align="center"> | <table border="1" cellpadding="8" width="85%" align="center"> | ||
| Line 219: | Line 223: | ||
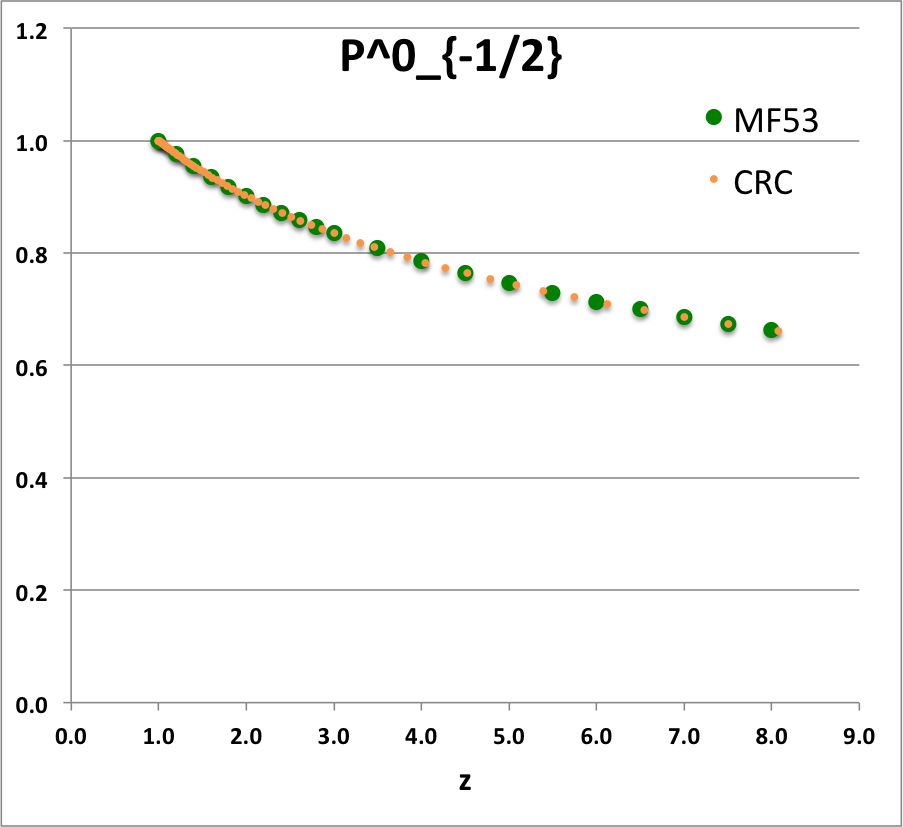
Expressions for the relevant toroidal functions are as follows: | Expressions for the relevant toroidal functions are as follows: | ||
{{ User:Tohline/Math/EQ_PminusHalf01 }} | |||
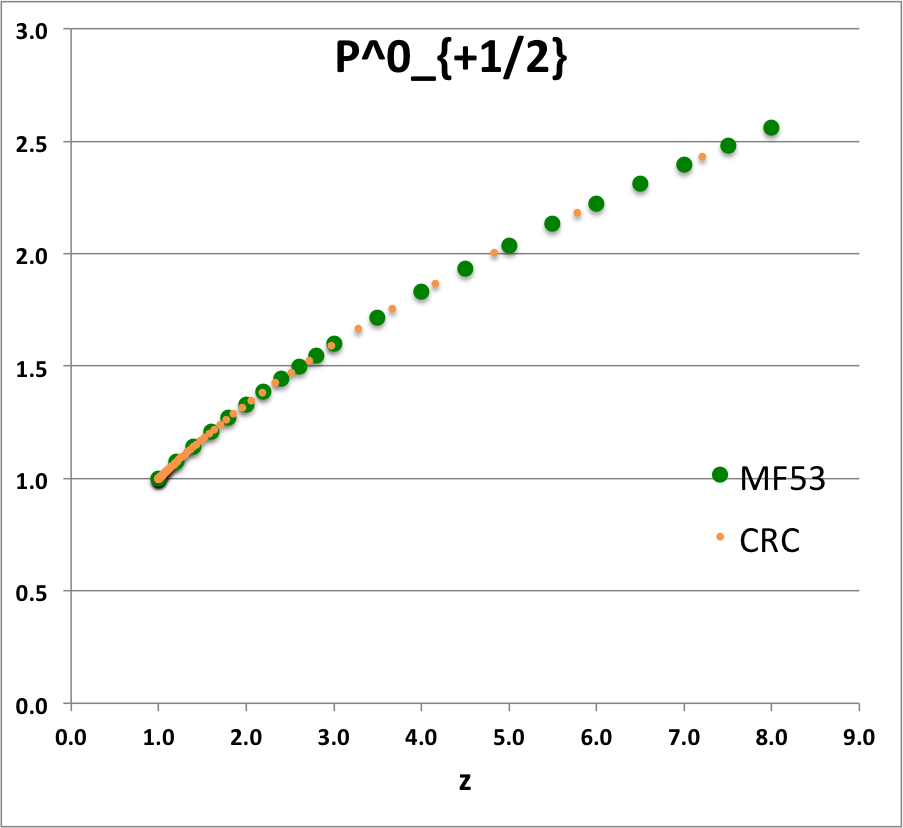
{{ User:Tohline/Math/EQ_PplusHalf01 }} | |||
<table align="center" cellpadding="5" border="1"> | |||
<tr> | <tr> | ||
<td align=" | <td align="center"><math>~P^0_{-\frac{1}{2}}(z)</math></td> | ||
<math>~ | <td align="center"><math>~P^0_{+\frac{1}{2}}(z)</math></td> | ||
</tr> | |||
<tr> | |||
<td align="center"> | |||
[[File:P0minusHalf.png|250px|P0minusHalf]] | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
[[File:P0plusHalf.png|250px|P0plusHalf]] | |||
</td> | </td> | ||
<td align="left"> | </tr> | ||
<tr> | |||
<td align="left" colspan="2"> | |||
See [[User:Tohline/Appendix/Equation_templates#Caption|relevant caption]]. | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
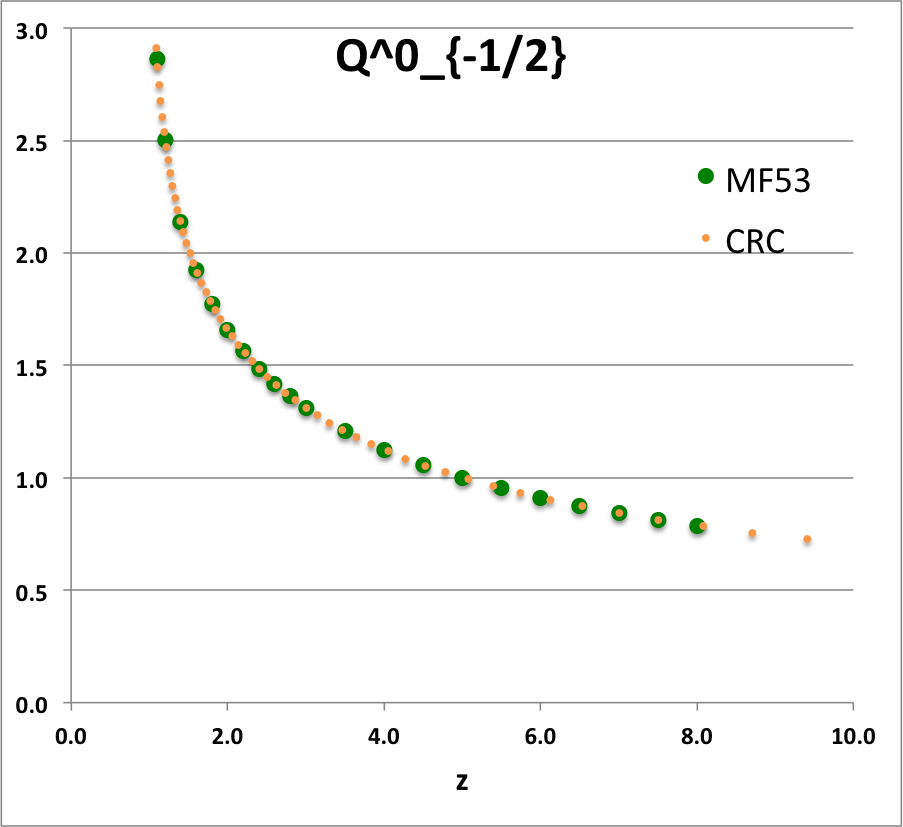
{{ User:Tohline/Math/EQ_QminusHalf01 }} | |||
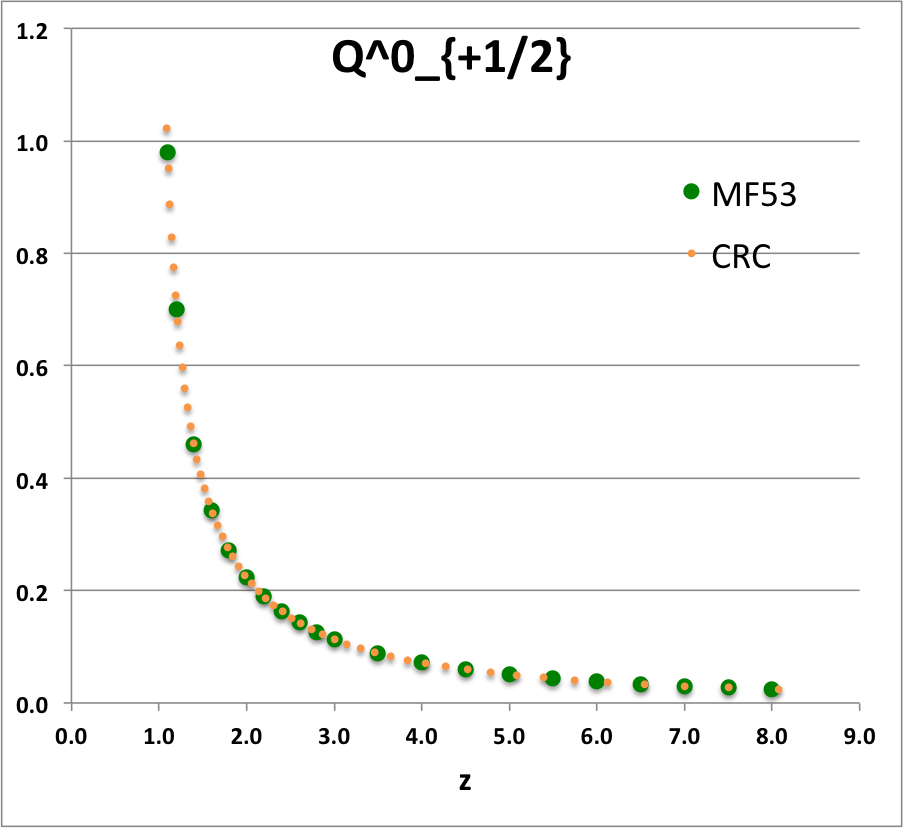
{{ User:Tohline/Math/EQ_QplusHalf01 }} | |||
where, <math>~K</math> and <math>~E</math> are complete elliptic integrals of the first and second kind, respectively. In equation (23) of [http://adsabs.harvard.edu/abs/1999ApJ...527...86C Cohl & Tohline (1999)], this last expression has been written in the more compact form, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~Q_{+\frac{1}{2}}(\chi)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 244: | Line 263: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \chi \mu K(\mu) - (1+\chi)\mu E(\mu) \, | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
where, <math>~\mu \equiv [2/(\chi + 1)]^{1 / 2}</math> and, for example, <math>~\chi = \cosh\eta</math>. | |||
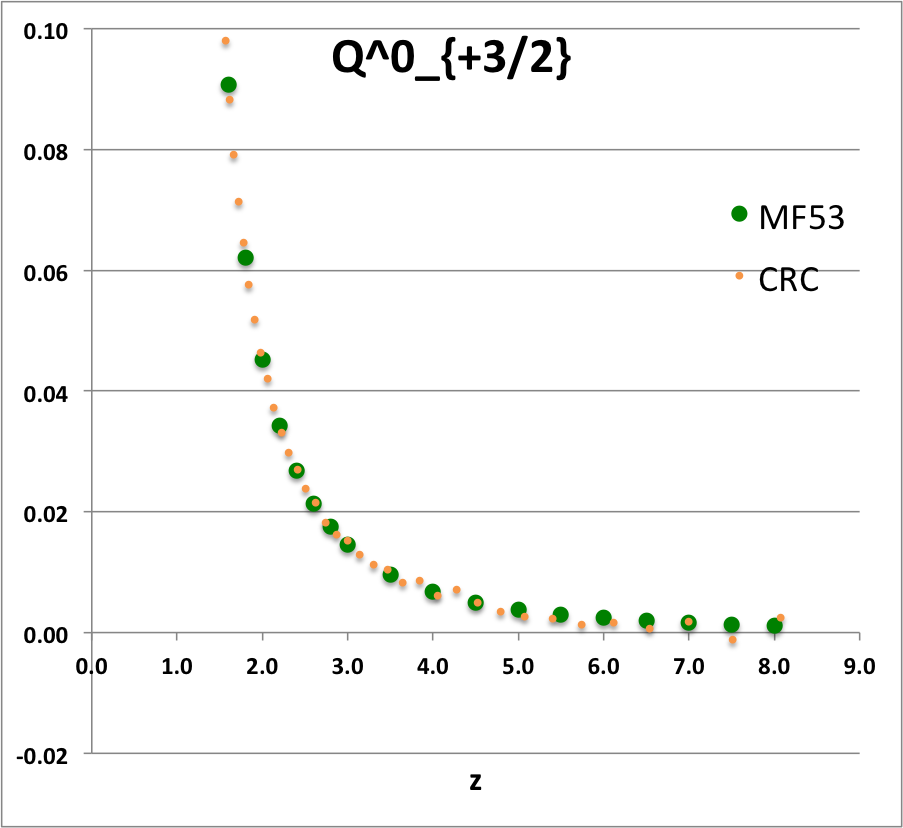
<table align="center" cellpadding="5" border="1"> | |||
<tr> | <tr> | ||
<td align=" | <td align="center"><math>~Q^0_{-\frac{1}{2}}(z)</math></td> | ||
<math>~ | <td align="center"><math>~Q^0_{+\frac{1}{2}}(z)</math></td> | ||
<td align="center"><math>~Q^0_{+\frac{3}{2}}(z)</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
[[File:Q0minus1Half.png|250px|P0minusHalf]] | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
[[File:Q0plus1Half.png|250px|P0plusHalf]] | |||
</td> | </td> | ||
<td align=" | <td align="center"> | ||
[[File:Q0plus3Half.png|250px|P0plusHalf]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="left" colspan="3"> | ||
See [[User:Tohline/Appendix/Equation_templates#Caption|relevant caption]]. | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
We also will employ the so-called ''recurrence relation'', | |||
{{ User:Tohline/Math/EQ_Toroidal04 }} | |||
After setting, <math>~\mu = 0</math>, and making the association, <math>~\nu \rightarrow (m - \tfrac{3}{2})</math>, for example, this gives, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 308: | Line 311: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
4\biggl[ \frac{m-1}{2m-1}\biggr] \chi Q_{m-\frac{3}{2}}(\chi) - \biggl[ \frac{2m-3}{2m-1}\biggr] Q_{m-\frac{5}{2}}(\chi) \, | 4\biggl[ \frac{m-1}{2m-1}\biggr] \chi Q_{m-\frac{3}{2}}(\chi) - \biggl[ \frac{2m-3}{2m-1}\biggr] Q_{m-\frac{5}{2}}(\chi) \, , | ||
</math> | </math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1999ApJ...527...86C Cohl & Tohline (1999)], §2.2.2, eq. (25) | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
which, for all <math>~m \ge 2</math> provides a means by which an expression for the associated toroidal function, <math>~Q_{m - \frac{1}{2}}</math>, can be generated from the foundation pair of expressions given above for <math>~Q_{- \frac{1}{2}}</math> and <math>~Q_{+ \frac{1}{2}}</math>. | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
===Asymptotic Behavior=== | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\lim_{\chi\rightarrow \infty} Q_{m-\frac{1}{2}}(\chi)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 330: | Line 338: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{\ | <math>~ | ||
\frac{\Gamma(m+\frac{1}{2}) \sqrt{\pi} }{ \Gamma(m+1) (2\chi)^{m+\frac{1}{2}} } | |||
</math> | |||
</td> | </td> | ||
</tr> | |||
</tr | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 353: | Line 352: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{\sqrt{\pi} }{ (2\chi)^{m+\frac{1}{2}} } \cdot \biggl[ \Gamma(m+\frac{1}{2}) \biggr] \biggl[ \Gamma(m+1) \biggr]^{-1} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 366: | Line 363: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \frac{\sqrt{\pi} }{ (2\chi)^{m+\frac{1}{2}} } \cdot \biggl[\frac{\sqrt{\pi}}{2^m} \cdot (2m-1)!! \biggr] \biggl[ m (m-1)! \biggr]^{-1} | ||
\biggr | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 385: | Line 380: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2^{ | \frac{\pi }{2^{2m+\frac{1}{2}} \chi^{m+\frac{1}{2}} } \cdot \biggl[ \frac{(2m-1)!! }{ m (m-1)! }\biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr><th align="center" colspan="2"> | |||
Asymptotic behavior: | |||
</th></tr> | |||
<tr> | |||
<td align="center"><math>~m</math></td> | |||
<td align="center" colspan="1"> | |||
<math>~\lim_{\chi\rightarrow \infty} Q_{m-\frac{1}{2}}(\chi)</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align=" | <td align="center">0</td> | ||
<td align="center"> | |||
<math>~ | |||
\frac{\Gamma(\frac{1}{2}) \sqrt{\pi} }{ \Gamma(1) (2\chi)^{\frac{1}{2}} } | |||
= \frac{\pi}{ (2\chi)^{1 / 2} } \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | |||
<tr> | |||
<td align="center">1</td> | |||
<td align="center"> | <td align="center"> | ||
<math>~ | |||
\frac{\pi }{2^{5/2} \chi^{3/2} } | |||
</math> | |||
</td> | </td> | ||
<td align=" | </tr> | ||
<tr> | |||
<td align="center">2</td> | |||
<td align="center"> | |||
<math>~ | <math>~ | ||
\ | \frac{\pi }{2^{\frac{9}{2}} \chi^{\frac{5}{2}} } \cdot \biggl[ \frac{(3)!! }{ 2 }\biggr] | ||
= | |||
\frac{360~\pi }{2^{9/2} \chi^{5/2} } | |||
= | |||
\frac{45~\pi }{2^{3/2} \chi^{5/2} } | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
===Dimensionless Potential Expression=== | |||
Given that the portion of the leading term in Wong's expression that sits inside the square brackets is equivalent to the density, <math>~\rho_0 = M/V</math>, of the torus material — that is, given that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{1}{2\pi^2 a^2}\biggl(\frac{M}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 417: | Line 442: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\rho_0 V}{2\pi^2 a^3} \biggl[ \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] </math> | ||
\frac{\ | |||
\biggr | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | |||
<td align="center"> | |||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\rho_0\, ,</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
— a reasonable dimensionless version of Wong's expression could be obtained by dividing through by the quantity, <math>~(G\rho_0 a^2) </math>. We prefer, instead, to normalize Wong's expression to the quantity, <math>~GM/R</math> , in which case the dimensionless version of the expression becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ \ | <math>~\frac{U(\eta^',\theta^')}{GM/R} \biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 462: | Line 465: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- | ||
\frac{2^{5 / 2} }{3} \biggl[ \frac{1}{2\pi^2}\biggl(\frac{R}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] \biggl\{ | |||
- \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] | |||
+~ (\cosh \eta^' - \cos \theta^')^{1 / 2} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 473: | Line 478: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') | |||
Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 493: | Line 497: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- | ||
\frac{2^{3 / 2} \sinh^2\eta_0 }{3\pi^2}\biggl\{ | |||
\ | - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] | ||
+~ (\cosh \eta^' - \cos \theta^')^{1 / 2} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') | ||
\ | Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) | ||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 527: | Line 526: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\sinh^2\eta_0 | ||
\ | \biggl\{ | ||
\ | \frac{\sinh^2\eta^'}{2 (\cosh \eta^' - \cos \theta^')^2} | ||
~- ~\frac{2^{3 / 2} }{3\pi^2} (\cosh \eta^' - \cos \theta^')^{1 / 2} | |||
\sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') | |||
Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) | |||
\biggr\} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
===Prior to the Integration=== | |||
The Green's function written in toroidal coordinates is, | |||
<table border="0" align="center" cellpadding="5"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 556: | Line 554: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
where,<br /> | |||
<div align="center"><math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'} \, ,</math> | |||
</div> | |||
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a ''toroidal'' function of zeroth order. Hence, a valid expression for the gravitational potential is, | |||
<table border="0" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~ \Phi_B(\varpi,\phi,z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 568: | Line 574: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~ | ||
-G \int \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 574: | Line 582: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 580: | Line 588: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~ | ||
-G \int \biggl\{ | |||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) | |||
\biggr\}~ | |||
\rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-\frac{G}{\pi \sqrt{\varpi}} \int \rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' | |||
\sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
where, <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0=1</math> and <math>~\epsilon_m = 2</math> for <math>~m\ge 1</math>. | |||
---- | |||
Wong (1973) states that in toroidal coordinates the Green's function is, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 623: | Line 621: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 629: | Line 627: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~- | <math>~ | ||
\frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } | |||
\sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 638: | Line 639: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~- | <math>~ | ||
\ | \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta | ||
\, | \end{cases}\, , | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | <tr> | ||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.53) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "<font color="darkgreen">Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)</font>," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>, | |||
-- | |||
<div align="center"> | <div align="center"> | ||
| Line 658: | Line 662: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\eta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 664: | Line 668: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 673: | Line 674: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\cos\theta</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\tan\psi</math> | |||
</td> | </td> | ||
</tr> | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{y}{x} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | </table> | ||
</div> | </div> | ||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~r_1^2 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~r_2^2 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
and <math>~\theta</math> has the same sign as <math>~z</math>. | |||
Hence, the potential, <math>~U({\vec{r}}~')</math>, at a point <math>~{\vec{r}}~'</math> due to an arbitrary mass distribution, <math>~\rho({\vec{r}})</math>, is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~U({\vec{r}}~')</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 743: | Line 741: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~-G \iiint \frac{\rho(\vec{r}) d^3r}{|~\vec{r} - {\vec{r}}^{~'} ~|} \, .</math> | ||
-G \ | |||
\frac | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 760: | Line 753: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~-G \rho_0 a^3 | ||
\iiint \frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} \biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ | |||
\ | \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" | <td align="right"> | ||
[ | | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-G \rho_0 a^3\iiint | |||
\biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr]~d\eta~ d\theta~ d\psi~ </math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\times | ||
\frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } | |||
\sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta | ||
\end{cases} \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 811: | Line 804: | ||
</div> | </div> | ||
---- | |||
This should be compared with, | |||
<table border="0" align="center"> | |||
<tr> | |||
<table border="0 | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~ \Phi_B(\varpi,\phi,z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 830: | Line 816: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-G \iiint \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 838: | Line 824: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 844: | Line 830: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-G \iiint \biggl\{ | |||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) | |||
\biggr\}~ | |||
\rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 852: | Line 841: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 858: | Line 847: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | -\frac{G}{\pi \sqrt{\varpi}} \iiint\rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' | ||
\sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
---- | |||
The above expression for the potential of a uniform-density torus has been obtained by [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)] from the (double) integral expression, | |||
< | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~U(\eta^',\theta^')</math> | ||
( | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 896: | Line 871: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \frac{ | 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta | ||
\int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 903: | Line 879: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta | |||
\end{cases}\, | |||
</math> | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center" colspan="3"> | ||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.55) | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
which is valid for any azimuthal angle, <math>~\psi^'</math>. Notice that the step function, <math>~\Theta(\upsilon)</math>, no longer explicitly appears in this expression for the Coulomb (or gravitational) potential; it has been used to establish the specific limits on the "radial" coordinate integration. Next, he completes the integration over the angle, <math>~\theta</math>, to obtain, | |||
==CT99 Coordinates== | |||
<font color="red"><b>Eureka!</b></font> Via his dogged efforts and an extraordinarily in-depth investigation of this problem, [[User:Tohline/Appendix/Ramblings/CCGF#Compact_Cylindrical_Green_Function_.28CCGF.29|in 1999 Howard S. Cohl discovered]] that, in cylindrical coordinates, the relevant Green's function can be written in a much more compact and much more practical form. Specifically, he realized that, | |||
<table border="0" align="center" cellpadding="5"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 948: | Line 912: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
where,<br /> | |||
<div align="center"><math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'} \, ,</math><br /><br /> | |||
[http://adsabs.harvard.edu/abs/1999ApJ...527...86C H. S. Cohl & J. E. Tohline (1999)], p. 88, Eqs. (15) & (16)<br /> | |||
See also: [http://adsabs.harvard.edu/abs/2007AmJPh..75..724S Selvaggi, Salon & Chari (2007)] §II, eq. (5)<br /> | |||
and the [https://dlmf.nist.gov/14.19#ii DLMF's definition of Toroidal Functions], <math>~Q_{m - 1 / 2}^{0}</math> | |||
</div> | |||
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a ''toroidal'' function of zeroth order; see [[#Toroidal_Functions|additional details, below]]. Hence, anywhere along the boundary of our cylindrical-coordinate mesh, a valid expression for the gravitational potential is, | |||
<table border="0" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ \Phi_B(\varpi,\phi,z)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 963: | Line 935: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-G \int \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 987: | Line 949: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl | <math>~ | ||
-G \int \biggl\{ | |||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) | |||
\biggr\}~ | |||
\rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 993: | Line 960: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,002: | Line 966: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
-\frac{G}{\pi \sqrt{\varpi}} \int \rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' | |||
\sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1999ApJ...527...86C H. S. Cohl & J. E. Tohline (1999)], p. 88, Eq. (18) | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
where, <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0=1</math> and <math>~\epsilon_m = 2</math> for <math>~m\ge 1</math>. Following this discovery, most of my research group's 3D numerical modeling of self-gravitating fluids has been conducted using ''Toroidal functions'' instead of ''Spherical Harmonics'' to evaluate the boundary potential on our cylindrical-coordinate meshes. | |||
In our [[User:Tohline/2DStructure/ToroidalCoordinates#Statement_of_the_Problem|accompanying statement of this problem]], we have written, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Phi(R_*,Z_*)</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,018: | Line 992: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- \frac{2G}{R_*^{1 / 2}} \int\int \varpi^{1 / 2} \mu K(\mu) \rho(\varpi, Z) d\varpi dZ \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
where, <math>~K(\mu)</math> is the complete elliptic integral of the first kind, and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mu^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Observer Toroidal Coordinates== | |||
=Our Mucking Around= | |||
Begins on p. 332 of [https://books.google.com/books?id=MtU8uP7XMvoC&printsec=frontcover&dq=Abramowitz+and+stegun&hl=en&sa=X&ved=0ahUKEwialra5xNbaAhWKna0KHcLAASAQ6AEILDAA#v=onepage&q=Abramowitz%20and%20stegun&f=false M. Abramowitz & I. A. Stegun (1995)] | |||
==Recurrence Relations== | |||
According to [https://books.google.com/books?id=MtU8uP7XMvoC&printsec=frontcover&dq=Abramowitz+and+stegun&hl=en&sa=X&ved=0ahUKEwialra5xNbaAhWKna0KHcLAASAQ6AEILDAA#v=onepage&q=Abramowitz%20and%20stegun&f=false M. Abramowitz & I. A. Stegun (1995)], both <math>~P_\nu^\mu</math> and <math>~Q_\nu^\mu</math> satisfy the same recurrence relations. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P_\nu^{\mu+1}(z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,043: | Line 1,037: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
(2\nu | (z^2 - 1)^{- 1 / 2} \biggl[ (\nu - \mu)z P_\nu^\mu(z) - (\nu + \mu)P_{\nu - 1}^\mu(z) \biggr] \, ; | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,050: | Line 1,044: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~(z^2-1) \frac{dP_\nu^{\mu}(z)}{dz}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,057: | Line 1,051: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | (\nu + \mu)(\nu - \mu +1_(z^2-1)^{1 / 2} P_\nu^{\mu - 1}(z) - \mu zP_\nu^\mu(z) \, ; | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,064: | Line 1,058: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~(\nu - \mu + 1)P_{\nu + 1}^{\mu}(z)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,071: | Line 1,065: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | (2\nu+1)zP_\nu^\mu (z) -(\nu + \mu)P_{\nu-1}^\mu(z) \, ; | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~( | <math>~(z^2-1) \frac{dP_\nu^{\mu}(z)}{dz}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,090: | Line 1,079: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\nu z P_\nu^{\mu }(z) - (\nu + \mu)P_{\nu-1}^\mu(z) \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
<table border="1" cellpadding="5" align="center" width="90%"><tr><td align="left"> | |||
According to equation (14) of [https://www.jstor.org/stable/2369515?seq=1#page_scan_tab_contents A. B. Basset (1893, American Journal of Mathematics, vol. 15, No. 4, pp. 287 - 302)], | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~P_{-1 | <math>~ | ||
(n-m+\tfrac{1}{2})P_{n+1}^m(\nu) | |||
-2n\nu P_n^m(\nu) + \frac{(n-\tfrac{1}{2})^2}{(n-m-\tfrac{1}{2})}P_{n-1}^m(\nu) | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,110: | Line 1,102: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2 \ | \biggl[ \frac{m^2}{n-m-\tfrac{1}{2}} \biggr]P_{n-1}^m(\nu) | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,117: | Line 1,109: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~P_{+1 | <math>~\Rightarrow~~~ | ||
(n-m+\tfrac{1}{2})P_{n+1}^m(\nu) | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,124: | Line 1,118: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{ \ | 2n\nu P_n^m(\nu) | ||
+ \biggl[ \frac{m^2}{n-m-\tfrac{1}{2}} \biggr]P_{n-1}^m(\nu) | |||
- \frac{(n-\tfrac{1}{2})^2}{(n-m-\tfrac{1}{2})}P_{n-1}^m(\nu) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,131: | Line 1,127: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,138: | Line 1,134: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2 \ | 2n\nu P_n^m(\nu) | ||
+ \biggl[ \frac{m^2 - (n-\tfrac{1}{2})^2}{n-m-\tfrac{1}{2}} \biggr]P_{n-1}^m(\nu) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
After replacing, <math>~n</math>, with <math>~(n + \tfrac{1}{2})</math>, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow~~~ | ||
(n-m+1)P_{n+3 / 2}^m(\nu) | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,152: | Line 1,155: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{ \ | (2n+1)\nu P_{n+1 / 2}^m(\nu) | ||
+ \biggl[ \frac{m^2 - n^2}{n-m} \biggr]P_{n-1 / 2}^m(\nu) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
(2n+1)\nu P_{n+1 / 2}^m(\nu) | |||
- (n+m)P_{n-1 / 2}^m(\nu) \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | |||
</table> | |||
The ''coefficients'' of this last expression precisely match the coefficients in the above expression provided by [https://books.google.com/books?id=MtU8uP7XMvoC&printsec=frontcover&dq=Abramowitz+and+stegun&hl=en&sa=X&ved=0ahUKEwialra5xNbaAhWKna0KHcLAASAQ6AEILDAA#v=onepage&q=Abramowitz%20and%20stegun&f=false M. Abramowitz & I. A. Stegun (1995)], but the ''subscript'' notation is off by <math>~\tfrac{1}{2}</math>. This inconsistency most likely should be blamed on the notation adopted by Basset (1893). At the top of his p. 289 — which is a couple of pages before his equation (14) — Basset says: <font color="#009999">A toroidal function is an associated function of degree <math>~n - \tfrac{1}{2}</math> and order <math>~m</math>; and the notation which ought in strictness to be adopted for the two kinds of toroidal functions is <math>~P_{n-1 / 2}^m</math> and <math>~Q_{n-1 / 2}^m</math>; but as these functions rarely if ever occur in an investigation which also involves associated functions of integral degree <math>~n</math>, it will be generally sufficient to employ the suffix <math>~n</math> instead of <math>~n - \tfrac{1}{2}</math></font>. Thus, we probably should have shifted the ''subscript'' notation in his equation (14) by "-½" before incorporating our additional replacement everywhere of <math>~n</math> by <math>~(n + \tfrac{1}{2})</math>. | |||
<!-- | |||
— after replacing, <math>~n</math>, with <math>~(n - \tfrac{1}{2})</math>, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~( | <math>~[(n-\tfrac{1}{2}) - m + \tfrac{1}{2}]P_{(n-1 / 2)+1}^m(\nu) | ||
-2(n-\tfrac{1}{2})\nu P_{n-1 / 2}^m(\nu) | |||
+\frac{ [(n-\tfrac{1}{2})-\tfrac{1}{2}]^2 }{ [(n-\tfrac{1}{2}) - m - \tfrac{1}{2}] }P_{(n-1 / 2)-1}^m(\nu) | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{m^2}{(n-\tfrac{1}{2}) - m - \tfrac{1}{2}} \biggr]P_{(n-1 / 2)-1}^m(\nu)</math> | ||
1 - | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow~~~[n-m]P_{n+1 / 2}^m(\nu) | ||
-(2n-1)\nu P_{n-1 / 2}^m(\nu) | |||
+\frac{ [n-1]^2 }{ [n-m-1] }P_{n-3 / 2}^m(\nu) | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,204: | Line 1,208: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{m^2}{n-m-1} \biggr]P_{n-3 / 2}^m(\nu)</math> | ||
\frac{ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~P_{ | <math>~\Rightarrow~~~[n-m]P_{n+1 / 2}^m(\nu) | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,227: | Line 1,225: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | (2n-1)\nu P_{n-1 / 2}^m(\nu) | ||
+ \biggl[ \frac{m^2 -(n-1)^2}{n-m-1} \biggr]P_{n-3 / 2}^m(\nu) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
--> | |||
---- | |||
If we set <math>~\mu = 0</math> in the [https://books.google.com/books?id=MtU8uP7XMvoC&printsec=frontcover&dq=Abramowitz+and+stegun&hl=en&sa=X&ved=0ahUKEwialra5xNbaAhWKna0KHcLAASAQ6AEILDAA#v=onepage&q=Abramowitz%20and%20stegun&f=false M. Abramowitz & I. A. Stegun (1995)] recurrence relation, then replace <math>~\nu</math> everywhere with <math>~\nu - \tfrac{1}{2}</math>, we obtain, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~P_{ | <math>~(\nu + 1)P_{\nu + 1}(z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,241: | Line 1,249: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
(2\nu+1)zP_\nu (z) -(\nu )P_{\nu-1}(z) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\nu \rightarrow \nu - \tfrac{1}{2} ~~~\Rightarrow ~~~ (\nu + \tfrac{1}{2})P_{\nu + 1 / 2}(z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,267: | Line 1,263: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | (2\nu)zP_{\nu - 1 / 2} (z) -(\nu - \tfrac{1}{2})P_{\nu-3 / 2}(z) | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | Mult. thru by 2 <math>~~~\Rightarrow ~~~ (2\nu + 1)P_{\nu + 1 / 2}(z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | (4\nu)zP_{\nu - 1 / 2} (z) -(2\nu - 1)P_{\nu-3 / 2}(z) | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Independently, from equation (56) of [https://archive.org/stream/atreatiseonhydr02bassgoog#page/n44/mode/2up Basset's (1888, Cambridge: Beighton, Bell and Co.) ''A Treatise on Hydrodynamics''], we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~(2n+1)P_{n+1}(\nu) </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,298: | Line 1,296: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | 4nCP_n(\nu) - (2n-1)P_{n-1}(\nu) \, . | ||
</math> | </math> | ||
</td> | |||
</tr> | |||
</table> | |||
This matches the Abramowitz & Stegun expression if, as before, we employ the mapping, <math>~n \rightarrow n-\tfrac{1}{2}</math>, ''in the subscripts only''; also, note that, due to what must have been a typesetting error, the coefficient, <math>~C</math>, in Basset's expression must be replaced by the independent variable, <math>~\nu</math>. | |||
From equations (57) - (60) of [https://archive.org/stream/atreatiseonhydr02bassgoog#page/n44/mode/2up Basset's (1888) ''Hydrodynamics''], we also obtain, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_{-1 / 2} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,306: | Line 1,316: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2 \sqrt{k} ~F \, ; | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P_{+1 / 2} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,322: | Line 1,329: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{ \sqrt{k}}~ E \, ; | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~Q_{-1 / 2} | <math>~Q_{-1 / 2} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,344: | Line 1,344: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2 \sqrt{k} ~F \, ; | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,351: | Line 1,351: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~Q_{ | <math>~Q_{+1 / 2} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,357: | Line 1,357: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~2 | <math>~ | ||
~ | \frac{2}{ \sqrt{k}}~[ F - E] \, ; | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
where, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~k^2 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
e^{-2\eta} \, , | |||
</math> | </math> | ||
</td> | </td> | ||
< | <td align="center"> and </td> | ||
< | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~(k^')^2 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
1 - e^{-2\eta} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</td></tr></table> | |||
==Toroidal Functions== | |||
Relationship between one another, as per equation (8) in [http://adsabs.harvard.edu/abs/2000JCoPh.161..204G A. Gil, J. Segura, & N. M. Temme (2000, JCP, 161, 204 - 217)]: | |||
{{ User:Tohline/Math/EQ_Toroidal02 }} | |||
Note that the relationship between <math>~\lambda</math> and <math>~x</math> is the same as the relationship between <math>~\cosh\alpha</math> and <math>~\coth\alpha</math>, that is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\coth\alpha</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,419: | Line 1,413: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\pm \cosh\alpha}{ \sqrt{\cosh^2\alpha - 1}} \, ;</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
< | <td align="center"> or </td> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\cosh\alpha</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,438: | Line 1,423: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{\sqrt{1-\tanh^2\alpha}} </math> | ||
\frac{ | </td> | ||
< | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\pm \coth\alpha}{ \sqrt{\coth^2\alpha - 1 }} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Relation to Elliptic Integrals | |||
===PminusHalf01=== | |||
{{ User:Tohline/Math/EQ_PminusHalf01 }} | |||
<table border="1" cellpadding="5" align="center" width="80%"> | |||
<tr> | |||
<td align="center"> | |||
Proof that these are the same expressions: | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<td align="left"> | |||
From standard relationships between hyperbolic functions, we know that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{1}{\cosh u}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,453: | Line 1,462: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ 1 - \tanh^2u \biggr]^{1 / 2} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
So, if we let <math>~u \equiv \eta/2</math> and make the association, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\tanh u</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~~~\leftrightarrow~~~</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\sqrt{\frac{z-1}{z+1}} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,477: | Line 1,486: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ | <math>~\Rightarrow ~~~ \frac{1}{\cosh u}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,483: | Line 1,492: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl[ \frac{ | <math>~ | ||
\biggl[1 - \frac{z-1}{z+1} \biggr]^{1 / 2} | |||
</math> | </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,498: | Line 1,501: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[\frac{2}{z+1} \biggr]^{1 / 2} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Also, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\cosh \eta = \cosh(2u) = 2\cosh^2 u - 1</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,511: | Line 1,517: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~2\biggl[\frac{z+1}{2}\biggr] - 1 = z \, .</math> | ||
</td> | |||
</ | </tr> | ||
</table> | |||
Q.E.D. | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
<tr> | |||
<td align=" | ===QminusHalf01=== | ||
& | |||
{{ User:Tohline/Math/EQ_QminusHalf01 }} | |||
<div align="center"> | |||
<table border="1" cellpadding="5" align="center" width="80%"> | |||
<tr> | |||
<td align="center"> | |||
Proof that these are the same expressions: | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
Copying the Whipple's formula from [https://dlmf.nist.gov/14.19.v §14.19 of DLMF], | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\boldsymbol{Q}^{m}_{n-\frac{1}{2}}\left(\cosh\xi\right)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,526: | Line 1,552: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{\ | \frac{\Gamma\left(m-n+ | ||
\tfrac{1}{2}\right)}{\Gamma\left(m+n+\tfrac{1}{2}\right)}\left(\frac{\pi}{2 | |||
\sinh\xi}\right)^{1 / 2}P^{n}_{m-\frac{1}{2}}\left(\coth\xi\right) \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
then setting <math>~m = n = 0</math>, we have, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\boldsymbol{Q}^{0}_{-\frac{1}{2}}\left(\cosh\xi\right)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,547: | Line 1,571: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | \frac{\Gamma\left(\tfrac{1}{2}\right)}{\Gamma\left(\tfrac{1}{2}\right)}\left(\frac{\pi}{2\sinh\xi}\right)^{1 / 2}P^{0}_{-\frac{1}{2}}\left(\coth\xi\right) \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Step #1: Associate … <math>z \leftrightarrow \cosh\xi</math>. Then, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\boldsymbol{Q}^{0}_{-\frac{1}{2}}\left(\cosh\xi\right)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,571: | Line 1,588: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{ | \biggl(\frac{\pi}{2} \biggr)^{1/2} | ||
\left[\frac{1}{\sqrt{z^2-1}}\right]^{1 / 2} | |||
P^{0}_{-\frac{1}{2}}\biggl( \frac{z}{\sqrt{z^2-1}} \biggr) \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Step #2: Now making the association … <math>\Lambda \leftrightarrow z/\sqrt{z^2-1}</math>, we can write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~P_{ | <math>~P_{-1 / 2}(\Lambda)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,585: | Line 1,607: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{\pi} | \frac{2}{\pi} \biggl[\frac{2}{\Lambda+1}\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{\Lambda-1}{\Lambda+1}} \biggr) | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
z + \sqrt{z^2-1} | \frac{2}{\pi} \biggl[\frac{2\sqrt{z^2-1} }{z+\sqrt{z^2-1} }\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{z-\sqrt{z^2-1} }{z+\sqrt{z^2-1} }} \biggr) \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Step #3: Again, making the association … <math>z \leftrightarrow \cosh\xi</math>, means, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P_{-1 / 2}(\Lambda)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,625: | Line 1,638: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{\pi} \biggl[\frac{2\sinh\xi }{\cosh\xi+\sinh\xi }\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{\cosh\xi-\sinh\xi }{\cosh\xi+\sinh\xi }} \biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,632: | Line 1,645: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \boldsymbol{Q}^{0}_{-\frac{1}{2}}\left(\cosh\xi\right)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,638: | Line 1,651: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{\pi}{2\sinh\xi} \biggr]^{ 1 / 2} | ||
\frac{ | \frac{2}{\pi} \biggl[\frac{2\sinh\xi }{\cosh\xi+\sinh\xi }\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{\cosh\xi-\sinh\xi }{\cosh\xi+\sinh\xi }} \biggr) | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,653: | Line 1,666: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2[ | \frac{2}{\sqrt{\pi}} \biggl[\frac{1 }{\cosh\xi+\sinh\xi }\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{\cosh^2\xi-\sinh^2\xi }{(\cosh\xi+\sinh\xi)^2 }} \biggr) | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,667: | Line 1,680: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2\sqrt{ | \frac{2}{\sqrt{\pi}} \biggl[\frac{1 }{\cosh\xi+\sinh\xi }\biggr]^{1 / 2} ~K\biggl( \frac{1}{\cosh\xi+\sinh\xi } \biggr) | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,685: | Line 1,694: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{2}{\sqrt{\pi}} ~e^{-\xi/2} ~K( e^{-\xi}) \, , | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
which, apart from the leading factor of <math>~\pi^{-1 / 2}</math>, exactly matches the above expression. | |||
---- | |||
Note: From [http://hcohl.sdf.org/WHIPPLE.html Howard Cohl's online overview] — see, also, [[#Overview_by_Howard_Cohl|below]] — we find that the Whipple formula is slightly different from the one (quoted above) drawn from DLMF. According to Cohl the Whipple formula should be, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~Q_{n- 1 / 2}^m(\cosh\alpha)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,699: | Line 1,715: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | (-1)^m \Gamma (m - n + \tfrac{1}{2} )\biggl( \frac{\pi}{2\sinh\alpha} \biggr)^{1 / 2} P^{n}_{m - 1 / 2}(\coth\alpha) \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
The DLMF expression needs to be multiplied by <math>~(-1)^m\Gamma (m + n + \tfrac{1}{2} )</math> in order to match the expression provided by Cohl; for the case being considered here of <math>~m=n=0</math>, this factor is precisely <math>~\Gamma(\tfrac{1}{2}) = \sqrt{\pi}</math> — [https://en.wikipedia.org/wiki/Gamma_function#Properties see, for example, Wikipedia's discussion of the gamma function] — which cancels this confusing factor of <math>~\pi^{-1 / 2}</math>. | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===PplusHalf01=== | |||
{{ User:Tohline/Math/EQ_PplusHalf01 }} | |||
<div align="center"> | |||
<table border="1" cellpadding="5" align="center" width="80%"> | |||
<tr> | |||
<td align="center"> | |||
Proof that these are the same expressions: | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
If we associate, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~e^\eta</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~~~\leftrightarrow~~~</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
z + \sqrt{z^2-1} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,720: | Line 1,759: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~1 - e^{-2\eta}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,727: | Line 1,766: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
z \ | 1 - \frac{1}{[z + \sqrt{z^2-1}]^2} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,749: | Line 1,779: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2z^2 + 2z\sqrt{z^2-1} -2}{[z + \sqrt{z^2-1}]^2} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,773: | Line 1,794: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2 | \frac{2[z + \sqrt{z^2-1}] \sqrt{z^2-1}}{[z + \sqrt{z^2-1}]^2} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,780: | Line 1,801: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,787: | Line 1,808: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2} | \frac{2\sqrt{z^2-1}}{[z + \sqrt{z^2-1}]} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
It also means that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\cosh \eta = \tfrac{1}{2}[e^\eta + e^{-\eta}]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,801: | Line 1,826: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{1}{2}\biggl[z + \sqrt{z^2-1} + \frac{1}{z + \sqrt{z^2-1}} \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,808: | Line 1,833: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,815: | Line 1,840: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{1}{2}\biggl[\frac{z^2 + 2z\sqrt{z^2-1} + (z^2-1) + 1}{z + \sqrt{z^2-1}} \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,822: | Line 1,847: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,829: | Line 1,854: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{1}{2}\biggl[\frac{2z^2 + 2z\sqrt{z^2-1} }{z + \sqrt{z^2-1}} \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,852: | Line 1,868: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
z \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Q.E.D. | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<tr> | |||
<td align="right"> | ===QplusHalf01=== | ||
<math>~ | |||
</td> | {{ User:Tohline/Math/EQ_QplusHalf01 }} | ||
===Other=== | |||
When the argument, <math>~x</math>, lies in the range, <math>~-1 < x < 1</math>: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_{-1 / 2}(x)</math> | |||
</td> | |||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
| Line 1,866: | Line 1,899: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{\pi} ~K\biggl( \sqrt{ \frac{1-x}{2} } \biggr) \, ; | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,873: | Line 1,906: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~P_{-1 / 2}(\cos\theta)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,879: | Line 1,912: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{\pi} ~K\biggl( \sin \frac{\theta}{2}\biggr) \, ; | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~Q_{-1 / 2}(x)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,903: | Line 1,926: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
K\biggl( \sqrt{ \frac{1+x}{2} } \biggr) \, ; | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P_{+1 / 2}(x)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,917: | Line 1,940: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2}{\pi} \biggl[2E\biggl( \sqrt{ \frac{1-x}{2} } \biggr) - ~K\biggl( \sqrt{ \frac{1-x}{2} } \biggr) \biggr] \, ; | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~Q_{+ 1 / 2}(x)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,937: | Line 1,955: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | K\biggl( \sqrt{ \frac{1+x}{2} } \biggr) - 2E\biggl( \sqrt{ \frac{1+x}{2} } \biggr)\, ; | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
==Piece Together== | |||
When <math>~\mu = 0</math>, and <math>~\nu = (m- 3/ 2)</math>, the recurrence relation should be … | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~(m - \tfrac{1}{2})P_{m-1 / 2}(z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,954: | Line 1,978: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | [2m-2]zP_{m-3 / 2} (z) -(m - \tfrac{3}{2} )P_{m - 5 / 2} (z) | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~(2m -1)P_{m - 1 / 2}(z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,966: | Line 1,992: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
4(m-1)zP_{m - 3 /2 } (z) - (2m -3)P_{m-5 / 2} (z) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~P_{m - 1 / 2}(z)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,983: | Line 2,005: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{ | ||
4(m-1)zP_{m - 3 /2 } (z) - (2m -3)P_{m-5 / 2} (z) }{(2m -1)} \biggr] \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
for all <math>~m \ge 2</math>. | |||
=Overview by Howard Cohl= | |||
This subsection is drawn verbatim from [http://hcohl.sdf.org/WHIPPLE.html Howard Cohl's online overview] of toroidal functions. | |||
<font color="#009999"> | |||
… These last two expressions allow us to express toroidal functions of a certain kind (first or second, respectively) with argument hyperbolic cosine, as a direct proportionality in terms of the toroidal function of the other kind (second or first, respectively) with argument hyperbolic cotangent. The Whipple formulae may also be expressed as follows: | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~Q^n_{m- 1 / 2}(\cosh\alpha)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,001: | Line 2,029: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(-1)^n | ||
\frac{ | ~\Gamma(n-m + \tfrac{1}{2}) \biggl[ \frac{\pi}{2\sinh\alpha} \biggr]^{1 / 2} P^m_{n- 1 / 2}(\coth\alpha)\, , | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
< | <tr><td align="center" colspan="3">… and …</td></tr> | ||
<tr> | |||
<td align="right"> | |||
<math>~Q^n_{m- 1 / 2}(\coth\alpha)</math> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,019: | Line 2,043: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(-1)^m | ||
1 \, . | ~\frac{\pi}{\Gamma(m-n + \tfrac{1}{2})} \biggl[ \frac{\pi \sinh\alpha}{2} \biggr]^{1 / 2} P^m_{n- 1 / 2}(\cosh\alpha) \, . | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,026: | Line 2,050: | ||
</table> | </table> | ||
These interesting formulae have the property that they can relate Legendre functions of the first and second kinds directly in terms of each other. The only hitch is that you need a different argument to relate them. The way it works is as such. The Legendre functions of the first kind generally are well-behaved near the origin and blow up at positive infinity. Consequently the Legendre functions of the second kind blow up at unity and exponentially converges towards zero for large values of the argument. The relevant domain for toroidal functions is from 1 to infinity. The standard hyperbolic argument for these functions are naturally chosen to be the hyperbolic cosine since it ranges from 1 to infinity. The Whipple formulae relate the Legendre functions with argument 1 to infinity, cosh, to a reversed range given by the hyperbolic cotangent function. the hyperbolic cotangent function ranges from infinity at unity to unity at infinity. At what point alpha does cosh alpha equal coth alpha? The point alpha is given by | |||
<table border="0" cellpadding="5" align="center"> | |||
The | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ \ | <math>~\alpha</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,050: | Line 2,062: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \ln(1+\sqrt{2}) \cong 0.88137359 \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Therefore, <math>~e^\alpha</math> and <math>~e^{-\alpha}</math> are given, respectively, by | |||
<table border="0" cellpadding="5" align="center"> | |||
< | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~e^\alpha</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,093: | Line 2,080: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \sqrt{2} + 1 \cong 2.41421356 \, , | ||
</math> | </math> | ||
</td> | </td> | ||
<td align="center"> and </td> | |||
<td align=" | |||
and | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~e^{-\alpha}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,112: | Line 2,092: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \sqrt{2} - 1 \cong 0.41421356 \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
< | </table> | ||
The value that <math>~\cosh \alpha</math> and <math>~\coth \alpha</math> obtain at <math>~\alpha</math> is given by | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\cosh\alpha = \coth\alpha</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,130: | Line 2,110: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \sqrt{2} \cong 1.41421356 \, . | ||
\, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
< | The value that <math>~1/\cosh\alpha</math> and <math>~\tanh \alpha</math> obtain at <math>~\alpha</math> is given by | ||
<table border="0" cellpadding="5" align="center"> | |||
< | |||
</ | <tr> | ||
<td align="right"> | |||
<math>~\frac{1}{\cosh\alpha} = \tanh\alpha</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\sqrt{2}} \cong 0.70710678 \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Finally, <math>~\sinh \alpha</math> and it's inverse are given respectively by unity, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | |||
<math>~\sinh\alpha = \frac{1}{\sinh\alpha} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | <td align="left"> | ||
<math>~ | |||
1 \, . | |||
<math>~ | </math> | ||
</td> | |||
</tr> | |||
</table> | |||
We now see that the value at which the argument of the Legendre functions inversely maps the entire domain is given by cosh alpha = coth alpha ~ 1.4142356. By using the Whipple formulae for ring functions, we can inversely map the entire domain from 1 to infinity about this point cosh alpha, the square root of 2, and take full advantage of this new symmetry for Legendre functions. There being previously more definite and indefinite integrals tabulated for the Legendre function of the first kind than for the Legendre function of the second kind. In fact, this new transformation, when applied to toroidal functions yields distinct expressions which relate correspondingly the complete elliptic integrals of the first and second kind, which don't seem to be related to the linear and quadratic transformations of hypergeometric functions. | |||
</font> | |||
Note that, as shown above, [http://adsabs.harvard.edu/abs/2000JCoPh.161..204G Gil, ''et al.'' (2000)] state: | |||
{{ User:Tohline/Math/EQ_Toroidal02 }} | |||
Hence, if we swap the indexes, <math>~m\leftrightarrow n</math>, and make the assignments, <math>~x \leftrightarrow \cosh\alpha</math> and <math>~\lambda \leftrightarrow \coth\alpha</math>, this last relation becomes, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~Q_{m-1 / 2}^n (\coth\alpha)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(-1)^m | |||
\frac{\pi^{3/2}}{\sqrt{2} \Gamma(m-n+1 / 2)} (\cosh^2\alpha-1)^{1 / 4} P_{n-1 / 2}^m(\cosh\alpha) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(-1)^m | |||
\frac{\pi}{ \Gamma(m-n+1 / 2)} \biggl[ \frac{\pi\sinh\alpha }{2} \biggr]^{1 / 2} P_{n-1 / 2}^m(\cosh\alpha) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Alternatively, if we swap the indexes, <math>~m\leftrightarrow n</math>, and make the assignments, <math>~x \leftrightarrow \coth\alpha</math> and <math>~\lambda \leftrightarrow \cosh\alpha</math>, the [http://adsabs.harvard.edu/abs/2000JCoPh.161..204G Gil, ''et al.'' (2000)] relation becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~Q_{m-1 / 2}^n (\cosh\alpha)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(-1)^m | |||
\frac{\pi^{3/2}}{\sqrt{2} \Gamma(m-n+1 / 2)} (\coth^2\alpha-1)^{1 / 4} P_{n-1 / 2}^m(\coth\alpha) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(-1)^m | |||
\frac{\pi}{ \Gamma(m-n+1 / 2)} \biggl[ \frac{ \pi}{2\sinh\alpha} \biggr]^{1 / 2} P_{n-1 / 2}^m(\coth\alpha) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
However, in our situation the so-called "Euler reflection formula for gamma functions" gives the relation, | |||
{{ User:Tohline/Math/EQ_Gamma01 }} | |||
that is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\pi (-1)^{m}}{\Gamma(m-n+\frac{1}{2}) }</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(-1)^{n}\Gamma(n-m+\tfrac{1}{2}) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~Q_{m-1 / 2}^n (\cosh\alpha)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(-1)^{n}\Gamma(n-m+\tfrac{1}{2})\biggl[ \frac{ \pi}{2\sinh\alpha} \biggr]^{1 / 2} P_{n-1 / 2}^m(\coth\alpha) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
We see, then, that we are able to generate both of Cohl's relations from the Gil ''et al.'' relation. Yeah! | |||
=Drawn From Discussion of Solving the Poisson Equation= | |||
The following has been copied (May 2018) from an [[User:Tohline/AxisymmetricConfigurations/PoissonEq#Toroidal_Functions|accompanying chapter]] that presents the ''integral representation'' of the Poisson equation in terms of toroidal functions. | |||
<!-- NEW TABLE 3 --> | |||
<div align="center" id="Toroidal"> | |||
<table border="1" cellpadding="8" align="center" width="80%"> | |||
<tr> | |||
<th align="center"><font size="+0">Table 5: Green's Function in Terms of<br />Zero Order, Half-(Odd)Integer Degree, Associated Legendre Functions of the Second Kind, <math>~Q^0_{m-1 / 2}(\chi)</math><br />(also referred to as Toroidal Functions)</font></th> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
<table border="0" align="center" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where:<br /> | |||
<div align="center"><math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'}</math><br /><br /> | |||
[http://adsabs.harvard.edu/abs/1999ApJ...527...86C H. S. Cohl & J. E. Tohline (1999)], p. 88, Eqs. (15) & (16)<br /> | |||
See also the [https://dlmf.nist.gov/14.19#ii DLMF's definition of Toroidal Functions], <math>~Q_{m - 1 / 2}^{0}</math> | |||
</div> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
Note that, according to, for example, equation (8.731.5) of Gradshteyn & Ryzhik (1994), | |||
<div align="center"> | |||
<math>~Q^0_{-m - 1 / 2}(\chi) = Q^0_{m- 1 / 2}(\chi) \, .</math> | |||
</div> | |||
Hence, the Green's function can straightforwardly be rewritten in terms of a simpler summation over just ''non-negative'' values of the index, <math>~m</math>. | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
Referencing equations (8.13.3) and (8.13.7), respectively, of Abramowitz & Stegun (1965), we see that for the smallest two values of the ''non-negative'' index, <math>~m</math>, the function, <math>~Q_{m- 1 / 2}(\chi)</math>, can be rewritten in terms of, the more familiar, complete elliptic integrals of the first and second kind. Specifically, | |||
<table border="0" cellpadding="1" align="center" width="100%"> | |||
<tr> | |||
<td align="left" colspan="3"> | |||
for <math>~m = 0</math>, | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~Q_{m- 1 / 2}(\chi) ~\rightarrow~ Q_{-1 / 2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mu K(\mu) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="3"> | |||
and, for <math>~m = 1</math>, | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~Q_{m- 1 / 2}(\chi) ~\rightarrow~ Q_{+ 1 / 2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\chi \mu K(\mu) - (1+\chi)\mu E(\mu) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="3"> | |||
where, | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mu \equiv \biggl[ \frac{2}{1+\chi} \biggr]^{1 / 2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{4\varpi \varpi^'}{(\varpi + \varpi^')^2 + (z - z^')^2} \biggr]^{1 / 2} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
<div align="center"> | |||
Excerpt from p. 337 of [https://books.google.com/books?id=MtU8uP7XMvoC&printsec=frontcover&dq=Abramowitz+and+stegun&hl=en&sa=X&ved=0ahUKEwialra5xNbaAhWKna0KHcLAASAQ6AEILDAA#v=onepage&q=Abramowitz%20and%20stegun&f=false M. Abramowitz & I. A. Stegun (1995)] | |||
<!--, ''Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables''--> | |||
</div> | |||
[[File:AbramowitzStegun ToroidalFunctions2.png|center|700px|Abramowitz & Stegun (1965)]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
Finally, equation (8.5.3) from Abramowitz & Stegun (1965) or equation (8.832.4) of Gradshteyn & Ryzhik (1994) — also see equation (2) of [http://adsabs.harvard.edu/abs/2000JCoPh.161..204G Gil, Segura & Temme (2000)] — provide the recurrence relation for all other values of the index, <math>~m</math>. Specifically, for all <math>~m \ge 2</math>, | |||
<div align="center"> | |||
<math>~Q_{m - 1 / 2}(\chi) = 4\biggl[\frac{m-1}{2m-1}\biggr] \chi Q_{m- 3 / 2}(\chi) | |||
- \biggl[ \frac{2m-3}{2m-1}\biggr] Q_{m- 5 / 2}(\chi) \, .</math> | |||
</div> | |||
---- | |||
<div align="center"> | |||
Excerpt from p. 490 of [https://dl-acm-org.libezp.lib.lsu.edu/citation.cfm?id=365474&picked=prox W. Guatschi (1965, Communications of the ACM, 8, 488 - 492)] | |||
</div> | |||
[[File:ToroidalRecurrenceRelation.png|center|500px|Guatschi (1965, Communications of the ACM, 8, 488 - 492)]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=Just Compare Green Functions= | |||
==First Dabbling== | |||
According to [http://adsabs.harvard.edu/abs/1999ApJ...527...86C CT99], the Green's function written in toroidal coordinates is, | |||
<table border="0" align="center" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where,<br /> | |||
<div align="center"><math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'} \, ,</math> | |||
</div> | |||
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a ''toroidal'' function of zeroth order. | |||
From the [[User:Tohline/Apps/DysonWongTori#Introducing_Toroidal_Coordinates|Dyson-Wong Toroid]] chapter, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\varpi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{a \sinh\eta }{(\cosh\eta - \cos\theta)} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~z</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<span id="FirstDab">Hence, we can rewrite the Green's function as,</span> | |||
<table border="0" align="center" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\pi} | |||
\biggl[ \frac{a \sinh\eta^' }{(\cosh\eta^' - \cos\theta^')} \frac{a \sinh\eta }{(\cosh\eta - \cos\theta)}\biggr]^{- 1 / 2} | |||
\sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\pi a} [\sinh\eta^' \sinh\eta]^{- 1 / 2} | |||
\biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} | |||
\sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<!-- | |||
Hence, a valid expression for the gravitational potential is, | |||
<table border="0" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \Phi_B(\varpi,\phi,z)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-G \int \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-G \int \biggl\{ | |||
\frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) | |||
\biggr\}~ | |||
\rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\frac{G}{\pi \sqrt{\varpi}} \int \rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' | |||
\sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0=1</math> and <math>~\epsilon_m = 2</math> for <math>~m\ge 1</math>. | |||
--> | |||
---- | |||
Wong (1973) states that in toroidal coordinates the Green's function is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } | |||
\sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta | |||
\end{cases}\, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.53) | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "<font color="darkgreen">Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)</font>," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\cos\theta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tan\psi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{y}{x} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_1^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~r_2^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and <math>~\theta</math> has the same sign as <math>~z</math>. | |||
Note that: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\cosh\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2}\biggl[ e^\eta + e^{-\eta} \biggr] = ~\frac{1}{2}\biggl[ \frac{r_1}{r_2} + \frac{r_2}{r_1}\biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2}\biggl[ \frac{\sqrt{[ \varpi + a]^2 + z^2}}{\sqrt{[ \varpi - a]^2 + z^2}} | |||
+ \frac{\sqrt{[ \varpi - a]^2 + z^2}}{\sqrt{[ \varpi + a]^2 + z^2}}\biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ 4\cosh^2\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ \frac{ [( \varpi + a)^2 + z^2]^{1 / 2} }{ [( \varpi - a)^2 + z^2]^{1 / 2}} | |||
+ \frac{[( \varpi - a)^2 + z^2]^{1 / 2}}{ [( \varpi + a)^2 + z^2]^{1 / 2} }\biggr\}^2</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ 4\cosh^2\eta~ [( \varpi + a)^2 + z^2] [( \varpi - a)^2 + z^2]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ [( \varpi + a)^2 + z^2] | |||
+ [( \varpi - a)^2 + z^2] \biggr\}^2</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ 4\cosh^2\eta~ [ \varpi^2 + 2a\varpi + a^2 + z^2] [ \varpi^2 -2a\varpi + a^2 + z^2]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~4 [ \varpi^2 + a^2 + z^2]^2</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
\frac{ [ \varpi^2 + a^2 + z^2]^2}{\cosh^2\eta} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[ \varpi^4 -2a\varpi^3 + a^2\varpi^2 + \varpi^2 z^2 + 2a\varpi^3 - 4a^2\varpi^2 +2a^3\varpi + 2a\varpi z^2 + a^2\varpi^2 - 2a^3\varpi + a^4 + a^2z^2 + \varpi^2 z^2 -2a\varpi z^2 +a^2z^2 + z^4 ] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[ \varpi^4 + 2\varpi^2 z^2 - 2a^2\varpi^2 + a^4 + 2a^2z^2 + z^4 ] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Second Dabbling== | |||
If <math>~\eta = \ln(r_1/r_2)</math>, as defined by Wong, then we can show that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\coth\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This expression matches the expression for <math>~\Chi</math>, as defined in the CT99; see, for example, [[User:Tohline/2DStructure/ToroidalCoordinates#Statement_of_the_Problem|our accompanying discussion]], | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Chi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ \varpi^2 + R_*^2 + (Z_* -Z)^2 }{ 2R_*\varpi } \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
It is the context of the CT99 derivation that we state, | |||
<div align="center"> | |||
<math>Q_{-1/2}(\Chi)= Q_{-1/2}(\coth\eta) = \mu K(\mu) \, ,</math> | |||
</div> | |||
where the argument of the elliptic integral is related to <math>~\Chi</math> via the relation, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mu^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{2}{1+\Chi}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<table border="1" align="center" cellpadding="15" width="85%"> | |||
<tr> | |||
<td align="left"> | |||
In a [[User:Tohline/Appendix/Mathematics/ToroidalSynopsis01#SummaryTable|separate discussion]], we have derived expressions for the quantities, <math>~\Chi</math> and <math>~\mu^2</math>, in terms of Wong's toroidal coordinates. | |||
</td> | |||
</tr> | |||
</table> | |||
We note that, while the argument of the CT99 toroidal function is <math>~\coth\eta</math>, the argument of Wong's toroidal function is <math>~\cosh\eta</math>. It should be useful to keep in mind, therefore, that you can move back and forth between <math>~\coth\eta</math> and <math>~\cosh\eta</math> via the mapping (in either direction), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\lambda</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{ x }{ \sqrt{x^2-1} } \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, for example, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\cosh^2\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\coth^2\eta \biggl[ \coth^2\eta-1 \biggr]^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2} \biggl\{ \biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2}-1 \biggr\}^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl[ \frac{\varpi^2 + a^2 + z^2}{\cosh\eta} \biggr]^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~4a^2\varpi^2 \biggl\{ \biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2}-1 \biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ [ \varpi^2 + a^2 + z^2 ]^{2} - 4a^2\varpi^2 </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ ( \varpi^2 + a^2 + z^2 ) + 2a \varpi \biggr] \biggl[ ( \varpi^2 + a^2 + z^2 ) - 2a \varpi \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ [ (\varpi + a)^2 + z^2 ] [ (\varpi - a)^2 + z^2 ] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~\cosh\eta</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl\{ \frac{ [ \varpi^2 + a^2 + z^2 ]^2 }{ [ (\varpi + a)^2 + z^2 ] [ (\varpi - a)^2 + z^2 ] } \biggr\}^{1 / 2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So, according to Wong, for <math>~\eta^' > \eta</math>, the ''axisymmetric'' potential is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\eta^',\theta^')\biggr|_\mathrm{ axi }</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta | |||
\int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta | |||
\end{cases}\, | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
[http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], Eq. (2.55) | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~U(\eta^',\theta^')\biggr|_\mathrm{ axi }</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty | |||
\int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr] \sinh\eta ~P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~d\theta ~d\eta | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Drawing from equations (2.7), (2.17) and (2.18) of [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W Wong (1973)], we see that the volume,</span> <math>~V</math>, of a torus that is bounded by surface <math>~\eta_s</math> is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{V}{a^3} = \frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\iiint\limits_{\eta_s} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ = \frac{2\pi^2\cosh{\eta_s}}{\sinh^3\eta_s} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This means that, in toroidal coordinates, just the integration over the azimuthal angle, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2\pi \iint\limits \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
To be compared with the same expression in cylindrical coordinates, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{2\pi}{a^3} \iint\limits \varpi ~d\varpi ~dz \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This means that the coordinate mapping is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\varpi ~d\varpi ~dz}{a^3} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This means that the CT99 axisymmetric potential is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Phi(R_*,Z_*)\biggr|_\mathrm{ axi }</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 2G \iint \frac{Q_{-1/2}(\coth\eta)}{ (R_* \varpi)^{1 / 2}} \rho(\varpi, Z) ~\varpi~d\varpi dZ</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 2Ga^3 \iint \frac{Q_{-1/2}(\coth\eta)}{ (R_* \varpi)^{1 / 2}} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] \rho~d\eta~ d\theta</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Given that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{ 1 }{ \varpi }</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(\cosh\eta - \cos\theta)}{a \sinh\eta} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we therefore have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Phi(R_*,Z_*)\biggr|_\mathrm{ axi }</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 2Ga^2\biggl( \frac{a}{R_*}\biggr)^{1 / 2} \iint Q_{-1/2}(\coth\eta) \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^5} \biggr]^{1 / 2} \rho~d\eta~ d\theta</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Third Dabbling== | |||
From our [[#FirstDab|"First Dabbling" expression]] for the Green's Function, we have, | |||
<table border="0" align="center" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\pi a} [\sinh\eta^' \sinh\eta]^{- 1 / 2} | |||
\biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} | |||
\sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
And from our [[User:Tohline/Appendix/Mathematics/ToroidalConfusion#Joel.27s_Additional_Manipulations|examination of the summation expression]], we have found that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\sum_{n=0}^{\infty} \epsilon_n | |||
Q_{n-\frac{1}{2}}\left(\cosh\xi\right) \cos\left(n | |||
\phi\right) | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ | |||
\dfrac{ \pi/\sqrt{2} }{\left(\cosh\xi-\cos\phi\right)^{\frac{1}{2}} }\biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
\sum_{m=0}^{\infty} \epsilon_m | |||
Q_{m-\frac{1}{2}} | |||
\left(\cosh\xi\right) \cos\left[m( \phi - \phi^')\right] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{\pi}{\sqrt{2}} | |||
\biggl\{ \cosh\xi-\cos\left[( \phi - \phi^')\right]\biggr\}^{ - \frac{1}{2}} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
How does this jive with [[User:Tohline/Appendix/Mathematics/ToroidalSynopsis01#SummaryTable|our separate recognition]] that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr] \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Is it completely legitimate to make the association, <math>~\chi \leftrightarrow \cosh\xi</math> ? If so, then the Green's function becomes, | |||
<table border="0" align="center" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{a \sqrt{2}} [\sinh\eta^' \sinh\eta]^{- 1 / 2} | |||
\biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} | |||
\biggl\{ \biggl[ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr]-\cos\left[( \phi - \phi^')\right]\biggr\}^{ - \frac{1}{2}} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{a \sqrt{2}} | |||
\biggl[ \frac{ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta) }{ \sinh\eta^' \sinh\eta } \biggr]^{1 / 2} | |||
\biggl[ \frac{ \sinh\eta \cdot \sinh\eta^' }{\cosh\eta \cdot \cosh\eta^' - \sinh\eta \cdot \sinh\eta^'\cos ( \phi - \phi^') - \cos(\theta^' - \theta) } \biggr]^{ \frac{1}{2}} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{a \sqrt{2}} | |||
\biggl[ \frac{(\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta) }{\cosh\eta \cdot \cosh\eta^' - \sinh\eta \cdot \sinh\eta^'\cos ( \phi - \phi^') - \cos(\theta^' - \theta) } \biggr]^{ \frac{1}{2}} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
=See Also= | =See Also= | ||
Latest revision as of 17:41, 1 July 2018
Relationships Between Toroidal Functions

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Wong Toroidal Coordinates
Wong's Expression for the Potential
This chapter has been put together in an effort to lay the groundwork for an evaluation of Wong's (1973) derived expression for the gravitational potential both inside and outside of a uniform-density, axisymmetric torus. After multiplying his expression by the negative of <math>~G</math>, then replacing his total charge, <math>~q</math>, with the total mass, <math>~M</math>, Wong's interior (i.e., <math>~\eta^' > \eta_0</math>) solution is,
|
<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math> |
<math>~=</math> |
<math>~- \frac{2^{5 / 2} a^2 G}{3} \biggl[ \frac{1}{2\pi^2 a^2}\biggl(\frac{M}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] \biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math> |
|
|
|
<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} \, , </math> |
|
Wong (1973), Eq. (2.65) |
||
where,
|
<math>~B_n(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~ (n+\tfrac{1}{2})P_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) - (n-\tfrac{3}{2})P_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . </math> |
|
Wong (1973), Eq. (2.62) |
||
Summary of Toroidal Coordinates and Toroidal Functions
|
Summary |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Suppose you want to evaluate the potential of a uniform-density torus whose major radius is, <math>~R</math>, and minor cross-sectional radius is, <math>~d</math>. Evaluation of the potential can be relatively easily expressed in terms of a toroidal coordinate system, <math>~(\eta,\theta)</math>, whose "origin" is at a distance, <math>~a</math>, from the symmetry axis, where, <math>~a^2 \equiv R^2 - d^2 ~~~\Rightarrow ~~~ \frac{a^2}{d^2} = \frac{R^2}{d^2} - 1\, .</math>
The surface of the uniform-density torus is defined by the toroidal "radial" coordinate, <math>~\eta_0</math>, such that,
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The volume of a torus is, <math>~V = 2\pi R(\pi d^2) \, .</math> When this is rewritten in terms of our toroidal coordinate system, we have,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Expressions for the relevant toroidal functions are as follows:
where, <math>~K</math> and <math>~E</math> are complete elliptic integrals of the first and second kind, respectively. In equation (23) of Cohl & Tohline (1999), this last expression has been written in the more compact form,
where, <math>~\mu \equiv [2/(\chi + 1)]^{1 / 2}</math> and, for example, <math>~\chi = \cosh\eta</math>.
We also will employ the so-called recurrence relation,
After setting, <math>~\mu = 0</math>, and making the association, <math>~\nu \rightarrow (m - \tfrac{3}{2})</math>, for example, this gives,
which, for all <math>~m \ge 2</math> provides a means by which an expression for the associated toroidal function, <math>~Q_{m - \frac{1}{2}}</math>, can be generated from the foundation pair of expressions given above for <math>~Q_{- \frac{1}{2}}</math> and <math>~Q_{+ \frac{1}{2}}</math>. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Asymptotic Behavior
|
<math>~\lim_{\chi\rightarrow \infty} Q_{m-\frac{1}{2}}(\chi)</math> |
<math>~=</math> |
<math>~ \frac{\Gamma(m+\frac{1}{2}) \sqrt{\pi} }{ \Gamma(m+1) (2\chi)^{m+\frac{1}{2}} } </math> |
|
|
<math>~=</math> |
<math>~ \frac{\sqrt{\pi} }{ (2\chi)^{m+\frac{1}{2}} } \cdot \biggl[ \Gamma(m+\frac{1}{2}) \biggr] \biggl[ \Gamma(m+1) \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\sqrt{\pi} }{ (2\chi)^{m+\frac{1}{2}} } \cdot \biggl[\frac{\sqrt{\pi}}{2^m} \cdot (2m-1)!! \biggr] \biggl[ m (m-1)! \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\pi }{2^{2m+\frac{1}{2}} \chi^{m+\frac{1}{2}} } \cdot \biggl[ \frac{(2m-1)!! }{ m (m-1)! }\biggr] </math> |
|
Asymptotic behavior: | |
|---|---|
| <math>~m</math> |
<math>~\lim_{\chi\rightarrow \infty} Q_{m-\frac{1}{2}}(\chi)</math> |
| 0 |
<math>~ \frac{\Gamma(\frac{1}{2}) \sqrt{\pi} }{ \Gamma(1) (2\chi)^{\frac{1}{2}} } = \frac{\pi}{ (2\chi)^{1 / 2} } \, . </math> |
| 1 |
<math>~ \frac{\pi }{2^{5/2} \chi^{3/2} } </math> |
| 2 |
<math>~ \frac{\pi }{2^{\frac{9}{2}} \chi^{\frac{5}{2}} } \cdot \biggl[ \frac{(3)!! }{ 2 }\biggr] = \frac{360~\pi }{2^{9/2} \chi^{5/2} } = \frac{45~\pi }{2^{3/2} \chi^{5/2} } </math> |
Dimensionless Potential Expression
Given that the portion of the leading term in Wong's expression that sits inside the square brackets is equivalent to the density, <math>~\rho_0 = M/V</math>, of the torus material — that is, given that,
|
<math>~\frac{1}{2\pi^2 a^2}\biggl(\frac{M}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} </math> |
<math>~=</math> |
<math>~\frac{\rho_0 V}{2\pi^2 a^3} \biggl[ \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] </math> |
<math>~=</math> |
<math>~\rho_0\, ,</math> |
— a reasonable dimensionless version of Wong's expression could be obtained by dividing through by the quantity, <math>~(G\rho_0 a^2) </math>. We prefer, instead, to normalize Wong's expression to the quantity, <math>~GM/R</math> , in which case the dimensionless version of the expression becomes,
|
<math>~\frac{U(\eta^',\theta^')}{GM/R} \biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math> |
<math>~=</math> |
<math>~- \frac{2^{5 / 2} }{3} \biggl[ \frac{1}{2\pi^2}\biggl(\frac{R}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] \biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math> |
|
|
|
<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \frac{2^{3 / 2} \sinh^2\eta_0 }{3\pi^2}\biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math> |
|
|
|
<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\sinh^2\eta_0 \biggl\{ \frac{\sinh^2\eta^'}{2 (\cosh \eta^' - \cos \theta^')^2} ~- ~\frac{2^{3 / 2} }{3\pi^2} (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} \, . </math> |
Prior to the Integration
The Green's function written in toroidal coordinates is,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , </math> |
where,
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a toroidal function of zeroth order. Hence, a valid expression for the gravitational potential is,
|
<math>~ \Phi_B(\varpi,\phi,z)</math> |
<math>~=</math> |
<math>~ -G \int \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' </math> |
|
|
<math>~=</math> |
<math>~ -G \int \biggl\{ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \biggr\}~ \rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' </math> |
|
|
<math>~=</math> |
<math>~ -\frac{G}{\pi \sqrt{\varpi}} \int \rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math> |
where, <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0=1</math> and <math>~\epsilon_m = 2</math> for <math>~m\ge 1</math>.
Wong (1973) states that in toroidal coordinates the Green's function is,
|
<math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, , </math> |
|
Wong (1973), Eq. (2.53) |
||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>,
|
<math>~\eta</math> |
<math>~=</math> |
<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> |
|
<math>~\cos\theta</math> |
<math>~=</math> |
<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> |
|
<math>~\tan\psi</math> |
<math>~=</math> |
<math>~\frac{y}{x} \, ,</math> |
and,
|
<math>~r_1^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math> |
|
<math>~r_2^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math> |
and <math>~\theta</math> has the same sign as <math>~z</math>.
Hence, the potential, <math>~U({\vec{r}}~')</math>, at a point <math>~{\vec{r}}~'</math> due to an arbitrary mass distribution, <math>~\rho({\vec{r}})</math>, is,
|
<math>~U({\vec{r}}~')</math> |
<math>~=</math> |
<math>~-G \iiint \frac{\rho(\vec{r}) d^3r}{|~\vec{r} - {\vec{r}}^{~'} ~|} \, .</math> |
|
|
<math>~=</math> |
<math>~-G \rho_0 a^3 \iiint \frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} \biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ \, .</math> |
|
|
<math>~=</math> |
<math>~-G \rho_0 a^3\iiint \biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr]~d\eta~ d\theta~ d\psi~ </math> |
|
|
|
<math>~\times \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases} \biggr\} </math> |
This should be compared with,
|
<math>~ \Phi_B(\varpi,\phi,z)</math> |
<math>~=</math> |
<math>~ -G \iiint \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' </math> |
|
|
<math>~=</math> |
<math>~ -G \iiint \biggl\{ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \biggr\}~ \rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' </math> |
|
|
<math>~=</math> |
<math>~ -\frac{G}{\pi \sqrt{\varpi}} \iiint\rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math> |
The above expression for the potential of a uniform-density torus has been obtained by Wong (1973) from the (double) integral expression,
|
<math>~U(\eta^',\theta^')</math> |
<math>~=</math> |
<math>~ 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta \int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta </math> |
|
|
|
<math>~ \times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, </math> |
|
Wong (1973), Eq. (2.55) |
||
which is valid for any azimuthal angle, <math>~\psi^'</math>. Notice that the step function, <math>~\Theta(\upsilon)</math>, no longer explicitly appears in this expression for the Coulomb (or gravitational) potential; it has been used to establish the specific limits on the "radial" coordinate integration. Next, he completes the integration over the angle, <math>~\theta</math>, to obtain,
CT99 Coordinates
Eureka! Via his dogged efforts and an extraordinarily in-depth investigation of this problem, in 1999 Howard S. Cohl discovered that, in cylindrical coordinates, the relevant Green's function can be written in a much more compact and much more practical form. Specifically, he realized that,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , </math> |
where,
H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16)
See also: Selvaggi, Salon & Chari (2007) §II, eq. (5)
and the DLMF's definition of Toroidal Functions, <math>~Q_{m - 1 / 2}^{0}</math>
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a toroidal function of zeroth order; see additional details, below. Hence, anywhere along the boundary of our cylindrical-coordinate mesh, a valid expression for the gravitational potential is,
|
<math>~ \Phi_B(\varpi,\phi,z)</math> |
<math>~=</math> |
<math>~ -G \int \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' </math> |
|
|
<math>~=</math> |
<math>~ -G \int \biggl\{ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \biggr\}~ \rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' </math> |
|
|
<math>~=</math> |
<math>~ -\frac{G}{\pi \sqrt{\varpi}} \int \rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math> |
|
H. S. Cohl & J. E. Tohline (1999), p. 88, Eq. (18) |
||
where, <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0=1</math> and <math>~\epsilon_m = 2</math> for <math>~m\ge 1</math>. Following this discovery, most of my research group's 3D numerical modeling of self-gravitating fluids has been conducted using Toroidal functions instead of Spherical Harmonics to evaluate the boundary potential on our cylindrical-coordinate meshes.
In our accompanying statement of this problem, we have written,
|
<math>~\Phi(R_*,Z_*)</math> |
<math>~=</math> |
<math>~- \frac{2G}{R_*^{1 / 2}} \int\int \varpi^{1 / 2} \mu K(\mu) \rho(\varpi, Z) d\varpi dZ \, ,</math> |
where, <math>~K(\mu)</math> is the complete elliptic integral of the first kind, and,
|
<math>~\mu^2</math> |
<math>~=</math> |
<math>~ \biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . </math> |
Observer Toroidal Coordinates
Our Mucking Around
Begins on p. 332 of M. Abramowitz & I. A. Stegun (1995)
Recurrence Relations
According to M. Abramowitz & I. A. Stegun (1995), both <math>~P_\nu^\mu</math> and <math>~Q_\nu^\mu</math> satisfy the same recurrence relations.
|
<math>~P_\nu^{\mu+1}(z)</math> |
<math>~=</math> |
<math>~ (z^2 - 1)^{- 1 / 2} \biggl[ (\nu - \mu)z P_\nu^\mu(z) - (\nu + \mu)P_{\nu - 1}^\mu(z) \biggr] \, ; </math> |
|
<math>~(z^2-1) \frac{dP_\nu^{\mu}(z)}{dz}</math> |
<math>~=</math> |
<math>~ (\nu + \mu)(\nu - \mu +1_(z^2-1)^{1 / 2} P_\nu^{\mu - 1}(z) - \mu zP_\nu^\mu(z) \, ; </math> |
|
<math>~(\nu - \mu + 1)P_{\nu + 1}^{\mu}(z)</math> |
<math>~=</math> |
<math>~ (2\nu+1)zP_\nu^\mu (z) -(\nu + \mu)P_{\nu-1}^\mu(z) \, ; </math> |
|
<math>~(z^2-1) \frac{dP_\nu^{\mu}(z)}{dz}</math> |
<math>~=</math> |
<math>~ \nu z P_\nu^{\mu }(z) - (\nu + \mu)P_{\nu-1}^\mu(z) \, . </math> |
|
According to equation (14) of A. B. Basset (1893, American Journal of Mathematics, vol. 15, No. 4, pp. 287 - 302),
After replacing, <math>~n</math>, with <math>~(n + \tfrac{1}{2})</math>,
The coefficients of this last expression precisely match the coefficients in the above expression provided by M. Abramowitz & I. A. Stegun (1995), but the subscript notation is off by <math>~\tfrac{1}{2}</math>. This inconsistency most likely should be blamed on the notation adopted by Basset (1893). At the top of his p. 289 — which is a couple of pages before his equation (14) — Basset says: A toroidal function is an associated function of degree <math>~n - \tfrac{1}{2}</math> and order <math>~m</math>; and the notation which ought in strictness to be adopted for the two kinds of toroidal functions is <math>~P_{n-1 / 2}^m</math> and <math>~Q_{n-1 / 2}^m</math>; but as these functions rarely if ever occur in an investigation which also involves associated functions of integral degree <math>~n</math>, it will be generally sufficient to employ the suffix <math>~n</math> instead of <math>~n - \tfrac{1}{2}</math>. Thus, we probably should have shifted the subscript notation in his equation (14) by "-½" before incorporating our additional replacement everywhere of <math>~n</math> by <math>~(n + \tfrac{1}{2})</math>.
Independently, from equation (56) of Basset's (1888, Cambridge: Beighton, Bell and Co.) A Treatise on Hydrodynamics, we have,
This matches the Abramowitz & Stegun expression if, as before, we employ the mapping, <math>~n \rightarrow n-\tfrac{1}{2}</math>, in the subscripts only; also, note that, due to what must have been a typesetting error, the coefficient, <math>~C</math>, in Basset's expression must be replaced by the independent variable, <math>~\nu</math>. From equations (57) - (60) of Basset's (1888) Hydrodynamics, we also obtain,
where,
|
Toroidal Functions
Relationship between one another, as per equation (8) in A. Gil, J. Segura, & N. M. Temme (2000, JCP, 161, 204 - 217):
|
<math>~Q_{n-1 / 2}^m (\lambda)</math> |
<math>~=</math> |
<math>~(-1)^n \frac{\pi^{3/2}}{\sqrt{2}~ \Gamma(n-m+1 / 2)} (x^2-1)^{1 / 4} P_{m-1 / 2}^n(x) \, , </math> |
|
|
Gil, Segura, & Temme (2000): eq. (8) |
|||
| where: |
<math>~\lambda \equiv x/\sqrt{x^2-1}</math> |
Note that the relationship between <math>~\lambda</math> and <math>~x</math> is the same as the relationship between <math>~\cosh\alpha</math> and <math>~\coth\alpha</math>, that is,
|
<math>~\coth\alpha</math> |
<math>~=</math> |
<math>~\frac{\pm \cosh\alpha}{ \sqrt{\cosh^2\alpha - 1}} \, ;</math> |
or |
<math>~\cosh\alpha</math> |
<math>~=</math> |
<math>~\frac{1}{\sqrt{1-\tanh^2\alpha}} </math> |
<math>~=</math> |
<math>~\frac{\pm \coth\alpha}{ \sqrt{\coth^2\alpha - 1 }} \, .</math> |
Relation to Elliptic Integrals
PminusHalf01
|
<math>~P_{-\frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} \biggl[\frac{2}{z+1}\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{z-1}{z+1}} \biggr) </math> |
for example … |
<math>~P_{-\frac{1}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{\pi}{2} \cdot \cosh \frac{\eta}{2} \biggr]^{-1} K\biggl( \tanh \frac{\eta}{2} \biggr) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.1) |
Abramowitz & Stegun (1995), p. 337, eq. (8.13.2) |
||||||
|
Proof that these are the same expressions: |
||||||||||||||
|
From standard relationships between hyperbolic functions, we know that,
So, if we let <math>~u \equiv \eta/2</math> and make the association,
Also,
Q.E.D. |
QminusHalf01
|
<math>~Q_{-\frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ \sqrt{ \frac{2}{z+1} } ~K\biggl( \sqrt{ \frac{2}{z+1}} \biggr) </math> |
for example … |
<math>~Q_{-\frac{1}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ 2 e^{-\eta/2} K(e^{-\eta}) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.3) |
Abramowitz & Stegun (1995), p. 337, eq. (8.13.4) |
||||||
|
Proof that these are the same expressions: |
|||||||||||||||||||||||||||||||||
|
Copying the Whipple's formula from §14.19 of DLMF,
then setting <math>~m = n = 0</math>, we have,
Step #1: Associate … <math>z \leftrightarrow \cosh\xi</math>. Then,
Step #2: Now making the association … <math>\Lambda \leftrightarrow z/\sqrt{z^2-1}</math>, we can write,
Step #3: Again, making the association … <math>z \leftrightarrow \cosh\xi</math>, means,
which, apart from the leading factor of <math>~\pi^{-1 / 2}</math>, exactly matches the above expression. Note: From Howard Cohl's online overview — see, also, below — we find that the Whipple formula is slightly different from the one (quoted above) drawn from DLMF. According to Cohl the Whipple formula should be,
The DLMF expression needs to be multiplied by <math>~(-1)^m\Gamma (m + n + \tfrac{1}{2} )</math> in order to match the expression provided by Cohl; for the case being considered here of <math>~m=n=0</math>, this factor is precisely <math>~\Gamma(\tfrac{1}{2}) = \sqrt{\pi}</math> — see, for example, Wikipedia's discussion of the gamma function — which cancels this confusing factor of <math>~\pi^{-1 / 2}</math>. |
PplusHalf01
|
<math>~P_{+ \frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} \biggl[z + \sqrt{ z^2-1} \biggr]^{1 / 2} ~E\biggl( \sqrt{ \frac{2(z^2-1)^{1 / 2}}{z + (z^2-1)^{1 / 2}}} \biggr) </math> |
for example … |
<math>~P_{+ \frac{1}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi}~e^{\eta/2}~ E( \sqrt{1-e^{-2\eta}} ) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.5) |
Abramowitz & Stegun (1995), p. 337, eq. (8.13.6) |
||||||
|
Proof that these are the same expressions: |
|||||||||||||||||||||||||||
|
If we associate,
It also means that,
Q.E.D. |
QplusHalf01
|
<math>~Q_{+\frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ z \sqrt{ \frac{2}{z+1} }~K\biggl( \sqrt{ \frac{2}{z+1} } \biggr) ~-~ [2(z+1)]^{1 / 2} E\biggl( \sqrt{ \frac{2}{z+1} } \biggr) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.7) |
|||
Other
When the argument, <math>~x</math>, lies in the range, <math>~-1 < x < 1</math>:
|
<math>~P_{-1 / 2}(x)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} ~K\biggl( \sqrt{ \frac{1-x}{2} } \biggr) \, ; </math> |
|
<math>~P_{-1 / 2}(\cos\theta)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} ~K\biggl( \sin \frac{\theta}{2}\biggr) \, ; </math> |
|
<math>~Q_{-1 / 2}(x)</math> |
<math>~=</math> |
<math>~ K\biggl( \sqrt{ \frac{1+x}{2} } \biggr) \, ; </math> |
|
<math>~P_{+1 / 2}(x)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} \biggl[2E\biggl( \sqrt{ \frac{1-x}{2} } \biggr) - ~K\biggl( \sqrt{ \frac{1-x}{2} } \biggr) \biggr] \, ; </math> |
|
<math>~Q_{+ 1 / 2}(x)</math> |
<math>~=</math> |
<math>~ K\biggl( \sqrt{ \frac{1+x}{2} } \biggr) - 2E\biggl( \sqrt{ \frac{1+x}{2} } \biggr)\, ; </math> |
Piece Together
When <math>~\mu = 0</math>, and <math>~\nu = (m- 3/ 2)</math>, the recurrence relation should be …
|
<math>~(m - \tfrac{1}{2})P_{m-1 / 2}(z)</math> |
<math>~=</math> |
<math>~ [2m-2]zP_{m-3 / 2} (z) -(m - \tfrac{3}{2} )P_{m - 5 / 2} (z) </math> |
|
<math>~\Rightarrow ~~~(2m -1)P_{m - 1 / 2}(z)</math> |
<math>~=</math> |
<math>~ 4(m-1)zP_{m - 3 /2 } (z) - (2m -3)P_{m-5 / 2} (z) </math> |
|
<math>~\Rightarrow ~~~P_{m - 1 / 2}(z)</math> |
<math>~=</math> |
<math>~\biggl[ \frac{ 4(m-1)zP_{m - 3 /2 } (z) - (2m -3)P_{m-5 / 2} (z) }{(2m -1)} \biggr] \, , </math> |
for all <math>~m \ge 2</math>.
Overview by Howard Cohl
This subsection is drawn verbatim from Howard Cohl's online overview of toroidal functions.
… These last two expressions allow us to express toroidal functions of a certain kind (first or second, respectively) with argument hyperbolic cosine, as a direct proportionality in terms of the toroidal function of the other kind (second or first, respectively) with argument hyperbolic cotangent. The Whipple formulae may also be expressed as follows:
|
<math>~Q^n_{m- 1 / 2}(\cosh\alpha)</math> |
<math>~=</math> |
<math>~(-1)^n ~\Gamma(n-m + \tfrac{1}{2}) \biggl[ \frac{\pi}{2\sinh\alpha} \biggr]^{1 / 2} P^m_{n- 1 / 2}(\coth\alpha)\, , </math> |
| … and … | ||
|
<math>~Q^n_{m- 1 / 2}(\coth\alpha)</math> |
<math>~=</math> |
<math>~(-1)^m ~\frac{\pi}{\Gamma(m-n + \tfrac{1}{2})} \biggl[ \frac{\pi \sinh\alpha}{2} \biggr]^{1 / 2} P^m_{n- 1 / 2}(\cosh\alpha) \, . </math> |
These interesting formulae have the property that they can relate Legendre functions of the first and second kinds directly in terms of each other. The only hitch is that you need a different argument to relate them. The way it works is as such. The Legendre functions of the first kind generally are well-behaved near the origin and blow up at positive infinity. Consequently the Legendre functions of the second kind blow up at unity and exponentially converges towards zero for large values of the argument. The relevant domain for toroidal functions is from 1 to infinity. The standard hyperbolic argument for these functions are naturally chosen to be the hyperbolic cosine since it ranges from 1 to infinity. The Whipple formulae relate the Legendre functions with argument 1 to infinity, cosh, to a reversed range given by the hyperbolic cotangent function. the hyperbolic cotangent function ranges from infinity at unity to unity at infinity. At what point alpha does cosh alpha equal coth alpha? The point alpha is given by
|
<math>~\alpha</math> |
<math>~=</math> |
<math>~ \ln(1+\sqrt{2}) \cong 0.88137359 \, . </math> |
Therefore, <math>~e^\alpha</math> and <math>~e^{-\alpha}</math> are given, respectively, by
|
<math>~e^\alpha</math> |
<math>~=</math> |
<math>~ \sqrt{2} + 1 \cong 2.41421356 \, , </math> |
and |
<math>~e^{-\alpha}</math> |
<math>~=</math> |
<math>~ \sqrt{2} - 1 \cong 0.41421356 \, . </math> |
The value that <math>~\cosh \alpha</math> and <math>~\coth \alpha</math> obtain at <math>~\alpha</math> is given by
|
<math>~\cosh\alpha = \coth\alpha</math> |
<math>~=</math> |
<math>~ \sqrt{2} \cong 1.41421356 \, . </math> |
The value that <math>~1/\cosh\alpha</math> and <math>~\tanh \alpha</math> obtain at <math>~\alpha</math> is given by
|
<math>~\frac{1}{\cosh\alpha} = \tanh\alpha</math> |
<math>~=</math> |
<math>~ \frac{1}{\sqrt{2}} \cong 0.70710678 \, . </math> |
Finally, <math>~\sinh \alpha</math> and it's inverse are given respectively by unity,
|
<math>~\sinh\alpha = \frac{1}{\sinh\alpha} </math> |
<math>~=</math> |
<math>~ 1 \, . </math> |
We now see that the value at which the argument of the Legendre functions inversely maps the entire domain is given by cosh alpha = coth alpha ~ 1.4142356. By using the Whipple formulae for ring functions, we can inversely map the entire domain from 1 to infinity about this point cosh alpha, the square root of 2, and take full advantage of this new symmetry for Legendre functions. There being previously more definite and indefinite integrals tabulated for the Legendre function of the first kind than for the Legendre function of the second kind. In fact, this new transformation, when applied to toroidal functions yields distinct expressions which relate correspondingly the complete elliptic integrals of the first and second kind, which don't seem to be related to the linear and quadratic transformations of hypergeometric functions.
Note that, as shown above, Gil, et al. (2000) state:
|
<math>~Q_{n-1 / 2}^m (\lambda)</math> |
<math>~=</math> |
<math>~(-1)^n \frac{\pi^{3/2}}{\sqrt{2}~ \Gamma(n-m+1 / 2)} (x^2-1)^{1 / 4} P_{m-1 / 2}^n(x) \, , </math> |
|
|
Gil, Segura, & Temme (2000): eq. (8) |
|||
| where: |
<math>~\lambda \equiv x/\sqrt{x^2-1}</math> |
Hence, if we swap the indexes, <math>~m\leftrightarrow n</math>, and make the assignments, <math>~x \leftrightarrow \cosh\alpha</math> and <math>~\lambda \leftrightarrow \coth\alpha</math>, this last relation becomes,
|
<math>~Q_{m-1 / 2}^n (\coth\alpha)</math> |
<math>~=</math> |
<math>~(-1)^m \frac{\pi^{3/2}}{\sqrt{2} \Gamma(m-n+1 / 2)} (\cosh^2\alpha-1)^{1 / 4} P_{n-1 / 2}^m(\cosh\alpha) </math> |
|
|
<math>~=</math> |
<math>~(-1)^m \frac{\pi}{ \Gamma(m-n+1 / 2)} \biggl[ \frac{\pi\sinh\alpha }{2} \biggr]^{1 / 2} P_{n-1 / 2}^m(\cosh\alpha) </math> |
Alternatively, if we swap the indexes, <math>~m\leftrightarrow n</math>, and make the assignments, <math>~x \leftrightarrow \coth\alpha</math> and <math>~\lambda \leftrightarrow \cosh\alpha</math>, the Gil, et al. (2000) relation becomes,
|
<math>~Q_{m-1 / 2}^n (\cosh\alpha)</math> |
<math>~=</math> |
<math>~(-1)^m \frac{\pi^{3/2}}{\sqrt{2} \Gamma(m-n+1 / 2)} (\coth^2\alpha-1)^{1 / 4} P_{n-1 / 2}^m(\coth\alpha) </math> |
|
|
<math>~=</math> |
<math>~(-1)^m \frac{\pi}{ \Gamma(m-n+1 / 2)} \biggl[ \frac{ \pi}{2\sinh\alpha} \biggr]^{1 / 2} P_{n-1 / 2}^m(\coth\alpha) </math> |
However, in our situation the so-called "Euler reflection formula for gamma functions" gives the relation,
|
<math>~ \Gamma(z) ~\Gamma(1-z) </math> |
<math>~=</math> |
<math>~ \frac{\pi}{\sin(\pi z)} </math> |
<math>~\biggl|</math> |
for example, if
|
||||||||
| <math>~\biggl|</math> | ||||||||||||
| Valid for: |
<math>~z \ne0, \pm 1, \pm 2, </math> … |
<math>~\biggl|</math> | ||||||||||
that is,
|
<math>~\frac{\pi (-1)^{m}}{\Gamma(m-n+\frac{1}{2}) }</math> |
<math>~=</math> |
<math>~(-1)^{n}\Gamma(n-m+\tfrac{1}{2}) \, .</math> |
So,
|
<math>~Q_{m-1 / 2}^n (\cosh\alpha)</math> |
<math>~=</math> |
<math>~ (-1)^{n}\Gamma(n-m+\tfrac{1}{2})\biggl[ \frac{ \pi}{2\sinh\alpha} \biggr]^{1 / 2} P_{n-1 / 2}^m(\coth\alpha) </math> |
We see, then, that we are able to generate both of Cohl's relations from the Gil et al. relation. Yeah!
Drawn From Discussion of Solving the Poisson Equation
The following has been copied (May 2018) from an accompanying chapter that presents the integral representation of the Poisson equation in terms of toroidal functions.
| Table 5: Green's Function in Terms of Zero Order, Half-(Odd)Integer Degree, Associated Legendre Functions of the Second Kind, <math>~Q^0_{m-1 / 2}(\chi)</math> (also referred to as Toroidal Functions) |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
where: <math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'}</math>
H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16) |
||||||||||||||||||
|
Note that, according to, for example, equation (8.731.5) of Gradshteyn & Ryzhik (1994), <math>~Q^0_{-m - 1 / 2}(\chi) = Q^0_{m- 1 / 2}(\chi) \, .</math> Hence, the Green's function can straightforwardly be rewritten in terms of a simpler summation over just non-negative values of the index, <math>~m</math>. |
||||||||||||||||||
|
Referencing equations (8.13.3) and (8.13.7), respectively, of Abramowitz & Stegun (1965), we see that for the smallest two values of the non-negative index, <math>~m</math>, the function, <math>~Q_{m- 1 / 2}(\chi)</math>, can be rewritten in terms of, the more familiar, complete elliptic integrals of the first and second kind. Specifically,
Excerpt from p. 337 of M. Abramowitz & I. A. Stegun (1995) |
||||||||||||||||||
|
Finally, equation (8.5.3) from Abramowitz & Stegun (1965) or equation (8.832.4) of Gradshteyn & Ryzhik (1994) — also see equation (2) of Gil, Segura & Temme (2000) — provide the recurrence relation for all other values of the index, <math>~m</math>. Specifically, for all <math>~m \ge 2</math>, <math>~Q_{m - 1 / 2}(\chi) = 4\biggl[\frac{m-1}{2m-1}\biggr] \chi Q_{m- 3 / 2}(\chi) - \biggl[ \frac{2m-3}{2m-1}\biggr] Q_{m- 5 / 2}(\chi) \, .</math> Excerpt from p. 490 of W. Guatschi (1965, Communications of the ACM, 8, 488 - 492) |
||||||||||||||||||
Just Compare Green Functions
First Dabbling
According to CT99, the Green's function written in toroidal coordinates is,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math> |
where,
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a toroidal function of zeroth order.
From the Dyson-Wong Toroid chapter,
|
<math>~\varpi</math> |
<math>~=</math> |
<math>~\frac{a \sinh\eta }{(\cosh\eta - \cos\theta)} \, ,</math> |
|
<math>~z</math> |
<math>~=</math> |
<math>~\frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \, .</math> |
Hence, we can rewrite the Green's function as,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi} \biggl[ \frac{a \sinh\eta^' }{(\cosh\eta^' - \cos\theta^')} \frac{a \sinh\eta }{(\cosh\eta - \cos\theta)}\biggr]^{- 1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\pi a} [\sinh\eta^' \sinh\eta]^{- 1 / 2} \biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) </math> |
Wong (1973) states that in toroidal coordinates the Green's function is,
|
<math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, , </math> |
|
Wong (1973), Eq. (2.53) |
||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>,
|
<math>~\eta</math> |
<math>~=</math> |
<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> |
|
<math>~\cos\theta</math> |
<math>~=</math> |
<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> |
|
<math>~\tan\psi</math> |
<math>~=</math> |
<math>~\frac{y}{x} \, ,</math> |
and,
|
<math>~r_1^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math> |
|
<math>~r_2^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math> |
and <math>~\theta</math> has the same sign as <math>~z</math>.
Note that:
|
<math>~\cosh\eta</math> |
<math>~=</math> |
<math>~\frac{1}{2}\biggl[ e^\eta + e^{-\eta} \biggr] = ~\frac{1}{2}\biggl[ \frac{r_1}{r_2} + \frac{r_2}{r_1}\biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{2}\biggl[ \frac{\sqrt{[ \varpi + a]^2 + z^2}}{\sqrt{[ \varpi - a]^2 + z^2}} + \frac{\sqrt{[ \varpi - a]^2 + z^2}}{\sqrt{[ \varpi + a]^2 + z^2}}\biggr]</math> |
|
<math>~\Rightarrow ~~~ 4\cosh^2\eta</math> |
<math>~=</math> |
<math>~\biggl\{ \frac{ [( \varpi + a)^2 + z^2]^{1 / 2} }{ [( \varpi - a)^2 + z^2]^{1 / 2}} + \frac{[( \varpi - a)^2 + z^2]^{1 / 2}}{ [( \varpi + a)^2 + z^2]^{1 / 2} }\biggr\}^2</math> |
|
<math>~\Rightarrow ~~~ 4\cosh^2\eta~ [( \varpi + a)^2 + z^2] [( \varpi - a)^2 + z^2]</math> |
<math>~=</math> |
<math>~\biggl\{ [( \varpi + a)^2 + z^2] + [( \varpi - a)^2 + z^2] \biggr\}^2</math> |
|
<math>~\Rightarrow ~~~ 4\cosh^2\eta~ [ \varpi^2 + 2a\varpi + a^2 + z^2] [ \varpi^2 -2a\varpi + a^2 + z^2]</math> |
<math>~=</math> |
<math>~4 [ \varpi^2 + a^2 + z^2]^2</math> |
|
<math>~\Rightarrow ~~~ \frac{ [ \varpi^2 + a^2 + z^2]^2}{\cosh^2\eta} </math> |
<math>~=</math> |
<math>~ [ \varpi^4 -2a\varpi^3 + a^2\varpi^2 + \varpi^2 z^2 + 2a\varpi^3 - 4a^2\varpi^2 +2a^3\varpi + 2a\varpi z^2 + a^2\varpi^2 - 2a^3\varpi + a^4 + a^2z^2 + \varpi^2 z^2 -2a\varpi z^2 +a^2z^2 + z^4 ] </math> |
|
|
<math>~=</math> |
<math>~ [ \varpi^4 + 2\varpi^2 z^2 - 2a^2\varpi^2 + a^4 + 2a^2z^2 + z^4 ] </math> |
Second Dabbling
If <math>~\eta = \ln(r_1/r_2)</math>, as defined by Wong, then we can show that,
|
<math>~\coth\eta</math> |
<math>~=</math> |
<math>~ \frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \, . </math> |
This expression matches the expression for <math>~\Chi</math>, as defined in the CT99; see, for example, our accompanying discussion,
|
<math>~\Chi</math> |
<math>~=</math> |
<math>~ \frac{ \varpi^2 + R_*^2 + (Z_* -Z)^2 }{ 2R_*\varpi } \, . </math> |
It is the context of the CT99 derivation that we state,
<math>Q_{-1/2}(\Chi)= Q_{-1/2}(\coth\eta) = \mu K(\mu) \, ,</math>
where the argument of the elliptic integral is related to <math>~\Chi</math> via the relation,
|
<math>~\mu^2</math> |
<math>~\equiv</math> |
<math>~\frac{2}{1+\Chi}</math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . </math> |
|
In a separate discussion, we have derived expressions for the quantities, <math>~\Chi</math> and <math>~\mu^2</math>, in terms of Wong's toroidal coordinates. |
We note that, while the argument of the CT99 toroidal function is <math>~\coth\eta</math>, the argument of Wong's toroidal function is <math>~\cosh\eta</math>. It should be useful to keep in mind, therefore, that you can move back and forth between <math>~\coth\eta</math> and <math>~\cosh\eta</math> via the mapping (in either direction),
|
<math>~\lambda</math> |
<math>~=</math> |
<math>~\frac{ x }{ \sqrt{x^2-1} } \, .</math> |
Hence, for example, we have,
|
<math>~\cosh^2\eta</math> |
<math>~=</math> |
<math>~\coth^2\eta \biggl[ \coth^2\eta-1 \biggr]^{-1}</math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2} \biggl\{ \biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2}-1 \biggr\}^{-1}</math> |
|
<math>~\Rightarrow ~~~ \biggl[ \frac{\varpi^2 + a^2 + z^2}{\cosh\eta} \biggr]^2</math> |
<math>~=</math> |
<math>~4a^2\varpi^2 \biggl\{ \biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2}-1 \biggr\}</math> |
|
|
<math>~=</math> |
<math>~ [ \varpi^2 + a^2 + z^2 ]^{2} - 4a^2\varpi^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ ( \varpi^2 + a^2 + z^2 ) + 2a \varpi \biggr] \biggl[ ( \varpi^2 + a^2 + z^2 ) - 2a \varpi \biggr]</math> |
|
|
<math>~=</math> |
<math>~ [ (\varpi + a)^2 + z^2 ] [ (\varpi - a)^2 + z^2 ] </math> |
|
<math>~\Rightarrow ~~~\cosh\eta</math> |
<math>~=</math> |
<math>~ \biggl\{ \frac{ [ \varpi^2 + a^2 + z^2 ]^2 }{ [ (\varpi + a)^2 + z^2 ] [ (\varpi - a)^2 + z^2 ] } \biggr\}^{1 / 2} \, .</math> |
So, according to Wong, for <math>~\eta^' > \eta</math>, the axisymmetric potential is,
|
<math>~U(\eta^',\theta^')\biggr|_\mathrm{ axi }</math> |
<math>~=</math> |
<math>~ 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta \int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta </math> |
|
|
|
<math>~ \times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, </math> |
|
Wong (1973), Eq. (2.55) |
||
|
<math>~U(\eta^',\theta^')\biggr|_\mathrm{ axi }</math> |
<math>~=</math> |
<math>~ 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty \int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr] \sinh\eta ~P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~d\theta ~d\eta </math> |
Drawing from equations (2.7), (2.17) and (2.18) of Wong (1973), we see that the volume, <math>~V</math>, of a torus that is bounded by surface <math>~\eta_s</math> is,
|
<math>~\frac{V}{a^3} = \frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> |
<math>~=</math> |
<math>~\iiint\limits_{\eta_s} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ = \frac{2\pi^2\cosh{\eta_s}}{\sinh^3\eta_s} \, .</math> |
This means that, in toroidal coordinates, just the integration over the azimuthal angle,
|
<math>~\frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> |
<math>~=</math> |
<math>~2\pi \iint\limits \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta \, .</math> |
To be compared with the same expression in cylindrical coordinates,
|
<math>~\frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> |
<math>~=</math> |
<math>~\frac{2\pi}{a^3} \iint\limits \varpi ~d\varpi ~dz \, .</math> |
This means that the coordinate mapping is,
|
<math>~\frac{\varpi ~d\varpi ~dz}{a^3} </math> |
<math>~\leftrightarrow</math> |
<math>~\biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta \, .</math> |
This means that the CT99 axisymmetric potential is,
|
<math>~\Phi(R_*,Z_*)\biggr|_\mathrm{ axi }</math> |
<math>~=</math> |
<math>~- 2G \iint \frac{Q_{-1/2}(\coth\eta)}{ (R_* \varpi)^{1 / 2}} \rho(\varpi, Z) ~\varpi~d\varpi dZ</math> |
|
|
<math>~=</math> |
<math>~- 2Ga^3 \iint \frac{Q_{-1/2}(\coth\eta)}{ (R_* \varpi)^{1 / 2}} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] \rho~d\eta~ d\theta</math> |
Given that,
|
<math>~\frac{ 1 }{ \varpi }</math> |
<math>~=</math> |
<math>~\frac{(\cosh\eta - \cos\theta)}{a \sinh\eta} \, ,</math> |
we therefore have,
|
<math>~\Phi(R_*,Z_*)\biggr|_\mathrm{ axi }</math> |
<math>~=</math> |
<math>~- 2Ga^2\biggl( \frac{a}{R_*}\biggr)^{1 / 2} \iint Q_{-1/2}(\coth\eta) \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^5} \biggr]^{1 / 2} \rho~d\eta~ d\theta</math> |
Third Dabbling
From our "First Dabbling" expression for the Green's Function, we have,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} [\sinh\eta^' \sinh\eta]^{- 1 / 2} \biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, . </math> |
And from our examination of the summation expression, we have found that,
|
<math>~ \sum_{n=0}^{\infty} \epsilon_n Q_{n-\frac{1}{2}}\left(\cosh\xi\right) \cos\left(n \phi\right) </math> |
<math>~=</math> |
<math>~ \biggl[ \dfrac{ \pi/\sqrt{2} }{\left(\cosh\xi-\cos\phi\right)^{\frac{1}{2}} }\biggr] \, . </math> |
|
<math>~\Rightarrow ~~~ \sum_{m=0}^{\infty} \epsilon_m Q_{m-\frac{1}{2}} \left(\cosh\xi\right) \cos\left[m( \phi - \phi^')\right] </math> |
<math>~=</math> |
<math>~ \frac{\pi}{\sqrt{2}} \biggl\{ \cosh\xi-\cos\left[( \phi - \phi^')\right]\biggr\}^{ - \frac{1}{2}} \, . </math> |
How does this jive with our separate recognition that,
|
<math>~\chi</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr] \, ; </math> |
Is it completely legitimate to make the association, <math>~\chi \leftrightarrow \cosh\xi</math> ? If so, then the Green's function becomes,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{a \sqrt{2}} [\sinh\eta^' \sinh\eta]^{- 1 / 2} \biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} \biggl\{ \biggl[ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr]-\cos\left[( \phi - \phi^')\right]\biggr\}^{ - \frac{1}{2}} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{a \sqrt{2}} \biggl[ \frac{ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta) }{ \sinh\eta^' \sinh\eta } \biggr]^{1 / 2} \biggl[ \frac{ \sinh\eta \cdot \sinh\eta^' }{\cosh\eta \cdot \cosh\eta^' - \sinh\eta \cdot \sinh\eta^'\cos ( \phi - \phi^') - \cos(\theta^' - \theta) } \biggr]^{ \frac{1}{2}} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{a \sqrt{2}} \biggl[ \frac{(\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta) }{\cosh\eta \cdot \cosh\eta^' - \sinh\eta \cdot \sinh\eta^'\cos ( \phi - \phi^') - \cos(\theta^' - \theta) } \biggr]^{ \frac{1}{2}} \, . </math> |
See Also
- R. S. Maier (2017) — Associated Legendre Functions and Spherical Harmonics of Fractional Degree and Order
- R. S. Maier (2016, Proceedings of the Royal Society A, Vol. 472, Issue 2188, id. 20160097) — Legendre Functions of Fractional Degree: Transformations and Evaluations

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |