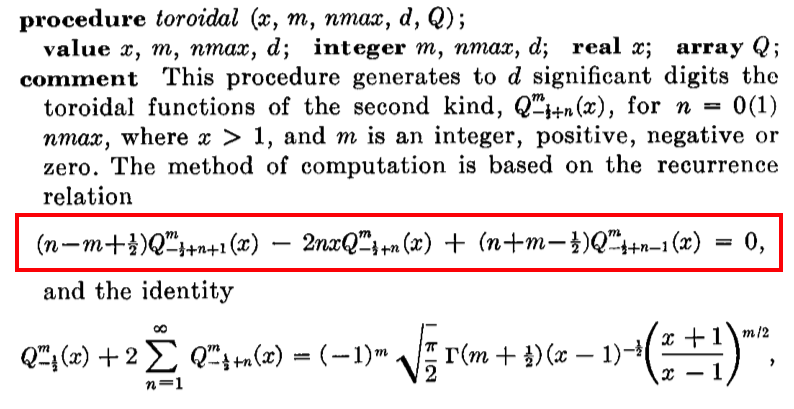User:Tohline/Appendix/Mathematics/ToroidalFunctions

Relationships Between Toroidal Functions

This chapter has been put together in an effort to lay the groundwork for an evaluation of Wong's (1973) derived expression for the gravitational potential both inside and outside of a uniform-density, axisymmetric torus. The interior (i.e., <math>~\eta^' > \eta_0</math>) solution is,

<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math>	<math>~=</math>	<math>~ \frac{2^{5 / 2} a^2}{3} \biggl[ \frac{1}{2\pi^2 a^2}\biggl(\frac{q}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] \biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math>
		<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} \, , </math>
Wong (1973), Eq. (2.65)

where,

<math>~B_n(\cosh\eta_0)</math>	<math>~\equiv</math>	<math>~ (n+\tfrac{1}{2})P_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) - (n-\tfrac{3}{2})P_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . </math>
Wong (1973), Eq. (2.62)

Our Mucking Around

Begins on p. 332 of M. Abramowitz & I. A. Stegun (1995)

Recurrence Relations

According to M. Abramowitz & I. A. Stegun (1995), both <math>~P_\nu^\mu</math> and <math>~Q_\nu^\mu</math> satisfy the same recurrence relations.

<math>~P_\nu^{\mu+1}(z)</math>	<math>~=</math>	<math>~ (z^2 - 1)^{- 1 / 2} \biggl[ (\nu - \mu)z P_\nu^\mu(z) - (\nu + \mu)P_{\nu - 1}^\mu(z) \biggr] \, ; </math>
<math>~(z^2-1) \frac{dP_\nu^{\mu}(z)}{dz}</math>	<math>~=</math>	<math>~ (\nu + \mu)(\nu - \mu +1_(z^2-1)^{1 / 2} P_\nu^{\mu - 1}(z) - \mu zP_\nu^\mu(z) \, ; </math>
<math>~(\nu - \mu + 1)P_{\nu + 1}^{\mu}(z)</math>	<math>~=</math>	<math>~ (2\nu+1)zP_\nu^\mu (z) -(\nu + \mu)P_{\nu-1}^\mu(z) \, ; </math>
<math>~(z^2-1) \frac{dP_\nu^{\mu}(z)}{dz}</math>	<math>~=</math>	<math>~ \nu z P_\nu^{\mu }(z) - (\nu + \mu)P_{\nu-1}^\mu(z) \, . </math>

According to equation (14) of A. B. Basset (1893, American Journal of Mathematics, vol. 15, No. 4, pp. 287 - 302), <math>~ (n-m+\tfrac{1}{2})P_{n+1}^m(\nu) -2n\nu P_n^m(\nu) + \frac{(n-\tfrac{1}{2})^2}{(n-m-\tfrac{1}{2})}P_{n-1}^m(\nu) </math> <math>~=</math> <math>~ \biggl[ \frac{m^2}{n-m-\tfrac{1}{2}} \biggr]P_{n-1}^m(\nu) </math> <math>~\Rightarrow~~~ (n-m+\tfrac{1}{2})P_{n+1}^m(\nu) </math> <math>~=</math> <math>~ 2n\nu P_n^m(\nu) + \biggl[ \frac{m^2}{n-m-\tfrac{1}{2}} \biggr]P_{n-1}^m(\nu) - \frac{(n-\tfrac{1}{2})^2}{(n-m-\tfrac{1}{2})}P_{n-1}^m(\nu) </math>   <math>~=</math> <math>~ 2n\nu P_n^m(\nu) + \biggl[ \frac{m^2 - (n-\tfrac{1}{2})^2}{n-m-\tfrac{1}{2}} \biggr]P_{n-1}^m(\nu) </math> After replacing, <math>~n</math>, with <math>~(n + \tfrac{1}{2})</math>, <math>~\Rightarrow~~~ (n-m+1)P_{n+3 / 2}^m(\nu) </math> <math>~=</math> <math>~ (2n+1)\nu P_{n+1 / 2}^m(\nu) + \biggl[ \frac{m^2 - n^2}{n-m} \biggr]P_{n-1 / 2}^m(\nu) </math>   <math>~=</math> <math>~ (2n+1)\nu P_{n+1 / 2}^m(\nu) - (n+m)P_{n-1 / 2}^m(\nu) \, . </math> The coefficients of this last expression precisely match the coefficients in the above expression provided by M. Abramowitz & I. A. Stegun (1995), but the subscript notation is off by <math>~\tfrac{1}{2}</math>. This inconsistency most likely should be blamed on the notation adopted by Basset (1893). At the top of his p. 289 — which is a couple of pages before his equation (14) — Basset says:   A toroidal function is an associated function of degree <math>~n - \tfrac{1}{2}</math> and order <math>~m</math>; and the notation which ought in strictness to be adopted for the two kinds of toroidal functions is <math>~P_{n-1 / 2}^m</math> and <math>~Q_{n-1 / 2}^m</math>; but as these functions rarely if ever occur in an investigation which also involves associated functions of integral degree <math>~n</math>, it will be generally sufficient to employ the suffix <math>~n</math> instead of <math>~n - \tfrac{1}{2}</math>. Thus, we probably should have shifted the subscript notation in his equation (14) by "-½" before incorporating our additional replacement everywhere of <math>~n</math> by <math>~(n + \tfrac{1}{2})</math>. If we set <math>~\mu = 0</math> in the M. Abramowitz & I. A. Stegun (1995) recurrence relation, then replace <math>~\nu</math> everywhere with <math>~\nu - \tfrac{1}{2}</math>, we obtain, <math>~(\nu + 1)P_{\nu + 1}(z)</math> <math>~=</math> <math>~ (2\nu+1)zP_\nu (z) -(\nu )P_{\nu-1}(z) </math> <math>~\nu \rightarrow \nu - \tfrac{1}{2} ~~~\Rightarrow ~~~ (\nu + \tfrac{1}{2})P_{\nu + 1 / 2}(z)</math> <math>~=</math> <math>~ (2\nu)zP_{\nu - 1 / 2} (z) -(\nu - \tfrac{1}{2})P_{\nu-3 / 2}(z) </math> Mult. thru by 2      <math>~~~\Rightarrow ~~~ (2\nu + 1)P_{\nu + 1 / 2}(z)</math> <math>~=</math> <math>~ (4\nu)zP_{\nu - 1 / 2} (z) -(2\nu - 1)P_{\nu-3 / 2}(z) </math> Independently, from equation (56) of Basset's (1888, Cambridge: Beighton, Bell and Co.) A Treatise on Hydrodynamics, we have, <math>~(2n+1)P_{n+1}(\nu) </math> <math>~=</math> <math>~ 4nCP_n(\nu) - (2n-1)P_{n-1}(\nu) \, . </math> This matches the Abramowitz & Stegun expression if, as before, we employ the mapping, <math>~n \rightarrow n-\tfrac{1}{2}</math>, in the subscripts only; also, note that, due to what must have been a typesetting error, the coefficient, <math>~C</math>, in Basset's expression must be replaced by the independent variable, <math>~\nu</math>. From equations (57) - (60) of Basset's (1888) Hydrodynamics, we also obtain, <math>~P_{-1 / 2} </math> <math>~=</math> <math>~ 2 \sqrt{k} ~F \, ; </math> <math>~P_{+1 / 2} </math> <math>~=</math> <math>~ \frac{2}{ \sqrt{k}}~ E \, ; </math> <math>~Q_{-1 / 2} </math> <math>~=</math> <math>~ 2 \sqrt{k} ~F \, ; </math> <math>~Q_{+1 / 2} </math> <math>~=</math> <math>~ \frac{2}{ \sqrt{k}}~[ F - E] \, ; </math> where, <math>~k^2 </math> <math>~\equiv</math> <math>~ e^{-2\eta} \, , </math>     and     <math>~(k^')^2 </math> <math>~\equiv</math> <math>~ 1 - e^{-2\eta} \, . </math>

Toroidal Functions

Relationship between one another, as per equation (8) in A. Gil, J. Segura, & N. M. Temme (2000, JCP, 161, 204 - 217):

<math>~Q_{n-1 / 2}^m (\lambda)</math>

<math>~=</math>

<math>~(-1)^n \frac{\pi^{3/2}}{\sqrt{2} \Gamma(n-m+1 / 2)} (x^2-1)^{1 / 4} P_{m-1 / 2}^n(x) \, , </math>

where, <math>~\lambda \equiv x/\sqrt{x^2-1}</math>.

Relation to Elliptic Integrals

<math>~P_{-1 / 2}(z)</math>	<math>~=</math>	<math>~ \frac{2}{\pi} \biggl[\frac{2}{z+1}\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{z-1}{z+1}} \biggr) \, ; </math>
<math>~P_{-1 / 2}(\cosh\eta)</math>	<math>~=</math>	<math>~ \biggl[\frac{\pi}{2}~\cosh\biggl(\frac{\eta}{2}\biggr)\biggr]^{-1} ~K\biggl( \tanh \frac{\eta}{2} \biggr) \, ; </math>

Proof that these are the same expressions:

<math>~\frac{1}{\cosh u}</math> <math>~=</math> <math>~ \biggl[ 1 - \tanh^2u \biggr]^{1 / 2} </math> So, if we associate, <math>~\tanh u</math> <math>~~~\leftrightarrow~~~</math> <math>~ \sqrt{\frac{z-1}{z+1}} </math> <math>~\Rightarrow ~~~ \frac{1}{\cosh u}</math> <math>~=</math> <math>~ \biggl[1 - \frac{z-1}{z+1} \biggr]^{1 / 2} </math> <math>~=</math> <math>~ \biggl[\frac{2}{z+1} \biggr]^{1 / 2} \, . </math>

<math>~Q_{-1 / 2}(z)</math>	<math>~=</math>	<math>~ \biggl[\frac{2}{z+1}\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{2}{z+1} }\biggr) \, ; </math>
<math>~Q_{-1 / 2}(\cosh\eta)</math>	<math>~=</math>	<math>~2 e^{- \eta / 2} ~K(e^{-\eta} ) \, ; </math>

Proof that these are the same expressions:

<math>~P_{+1 / 2}(z)</math>	<math>~=</math>	<math>~ \frac{2}{\pi} \biggl[ z + \sqrt{z^2-1} \biggr]^{1 / 2} ~E\biggl( \sqrt{ \frac{2(z^2-1)^{1 / 2}}{z + (z^2-1)^{1 / 2}}} \biggr) \, ; </math>
<math>~P_{+ 1 / 2}(\cosh\eta)</math>	<math>~=</math>	<math>~ \frac{2}{\pi}~e^{\eta/2} ~E\biggl( \sqrt{1-e^{-2\eta}} \biggr) \, ; </math>

Proof that these are the same expressions:

If we associate, <math>~e^\eta</math> <math>~~~\leftrightarrow~~~</math> <math>~ z + \sqrt{z^2-1} </math> <math>~\Rightarrow ~~~1 - e^{-2\eta}</math> <math>~=</math> <math>~ 1 - \frac{1}{[z + \sqrt{z^2-1}]^2} </math>   <math>~=</math> <math>~ \frac{2z^2 + 2z\sqrt{z^2-1} -2}{[z + \sqrt{z^2-1}]^2} </math>   <math>~=</math> <math>~ \frac{2[z + \sqrt{z^2-1}] \sqrt{z^2-1}}{[z + \sqrt{z^2-1}]^2} </math>   <math>~=</math> <math>~ \frac{2\sqrt{z^2-1}}{[z + \sqrt{z^2-1}]} \, . </math> It also means that, <math>~\cosh \eta = \tfrac{1}{2}[e^\eta + e^{-\eta}]</math> <math>~=</math> <math>~ \frac{1}{2}\biggl[z + \sqrt{z^2-1} + \frac{1}{z + \sqrt{z^2-1}} \biggr] </math>   <math>~=</math> <math>~ \frac{1}{2}\biggl[\frac{z^2 + 2z\sqrt{z^2-1} + (z^2-1) + 1}{z + \sqrt{z^2-1}} \biggr] </math>   <math>~=</math> <math>~ \frac{1}{2}\biggl[\frac{2z^2 + 2z\sqrt{z^2-1} }{z + \sqrt{z^2-1}} \biggr] </math>   <math>~=</math> <math>~ z \, . </math> Q.E.D.

<math>~Q_{+ 1 / 2}(z)</math>

<math>~=</math>

<math>~z \biggl[\frac{2}{z+1}\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{2}{z+1} }\biggr) - \biggl[2(z+1)\biggr]^{1 / 2} E\biggl( \sqrt{\frac{2}{z+1}} \biggr) \, . </math>

When the argument, <math>~x</math>, lies in the range, <math>~-1 < x < 1</math>:

<math>~P_{-1 / 2}(x)</math>	<math>~=</math>	<math>~ \frac{2}{\pi} ~K\biggl( \sqrt{ \frac{1-x}{2} } \biggr) \, ; </math>
<math>~P_{-1 / 2}(\cos\theta)</math>	<math>~=</math>	<math>~ \frac{2}{\pi} ~K\biggl( \sin \frac{\theta}{2}\biggr) \, ; </math>
<math>~Q_{-1 / 2}(x)</math>	<math>~=</math>	<math>~ K\biggl( \sqrt{ \frac{1+x}{2} } \biggr) \, ; </math>
<math>~P_{+1 / 2}(x)</math>	<math>~=</math>	<math>~ \frac{2}{\pi} \biggl[2E\biggl( \sqrt{ \frac{1-x}{2} } \biggr) - ~K\biggl( \sqrt{ \frac{1-x}{2} } \biggr) \biggr] \, ; </math>
<math>~Q_{+ 1 / 2}(x)</math>	<math>~=</math>	<math>~ K\biggl( \sqrt{ \frac{1+x}{2} } \biggr) - 2E\biggl( \sqrt{ \frac{1+x}{2} } \biggr)\, ; </math>

Piece Together

When <math>~\mu = 0</math>, and <math>~\nu = (m- 3/ 2)</math>, the recurrence relation should be …

<math>~(m - \tfrac{1}{2})P_{m-1 / 2}(z)</math>	<math>~=</math>	<math>~ [2m-2]zP_{m-3 / 2} (z) -(m - \tfrac{3}{2} )P_{m - 5 / 2} (z) </math>
<math>~\Rightarrow ~~~(2m -1)P_{m - 1 / 2}(z)</math>	<math>~=</math>	<math>~ 4(m-1)zP_{m - 3 /2 } (z) - (2m -3)P_{m-5 / 2} (z) </math>
<math>~\Rightarrow ~~~P_{m - 1 / 2}(z)</math>	<math>~=</math>	<math>~\biggl[ \frac{ 4(m-1)zP_{m - 3 /2 } (z) - (2m -3)P_{m-5 / 2} (z) }{(2m -1)} \biggr] \, , </math>

for all <math>~m \ge 2</math>.

Drawn From Discussion of Solving the Poisson Equation

The following has been copied (May 2018) from an accompanying chapter that presents the integral representation of the Poisson equation in terms of toroidal functions.

Table 5:  Green's Function in Terms of Zero Order, Half-(Odd)Integer Degree, Associated Legendre Functions of the Second Kind, <math>~Q^0_{m-1 / 2}(\chi)</math> (also referred to as Toroidal Functions)
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> <math>~=</math> <math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) </math> where: <math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'}</math> H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16) See also the DLMF's definition of Toroidal Functions, <math>~Q_{m - 1 / 2}^{0}</math>
Note that, according to, for example, equation (8.731.5) of Gradshteyn & Ryzhik (1994), <math>~Q^0_{-m - 1 / 2}(\chi) = Q^0_{m- 1 / 2}(\chi) \, .</math> Hence, the Green's function can straightforwardly be rewritten in terms of a simpler summation over just non-negative values of the index, <math>~m</math>.
Referencing equations (8.13.3) and (8.13.7), respectively, of Abramowitz & Stegun (1965), we see that for the smallest two values of the non-negative index, <math>~m</math>, the function, <math>~Q_{m- 1 / 2}(\chi)</math>, can be rewritten in terms of, the more familiar, complete elliptic integrals of the first and second kind. Specifically, for <math>~m = 0</math>, <math>~Q_{m- 1 / 2}(\chi) ~\rightarrow~ Q_{-1 / 2}</math> <math>~=</math> <math>~ \mu K(\mu) \, , </math> and, for <math>~m = 1</math>, <math>~Q_{m- 1 / 2}(\chi) ~\rightarrow~ Q_{+ 1 / 2}</math> <math>~=</math> <math>~ \chi \mu K(\mu) - (1+\chi)\mu E(\mu) \, , </math> where, <math>~\mu \equiv \biggl[ \frac{2}{1+\chi} \biggr]^{1 / 2}</math> <math>~=</math> <math>~ \biggl[ \frac{4\varpi \varpi^'}{(\varpi + \varpi^')^2 + (z - z^')^2} \biggr]^{1 / 2} \, . </math> Excerpt from p. 337 of M. Abramowitz & I. A. Stegun (1995)
Finally, equation (8.5.3) from Abramowitz & Stegun (1965) or equation (8.832.4) of Gradshteyn & Ryzhik (1994) — also see equation (2) of Gil, Segura & Temme (2000) — provide the recurrence relation for all other values of the index, <math>~m</math>. Specifically, for all <math>~m \ge 2</math>, <math>~Q_{m - 1 / 2}(\chi) = 4\biggl[\frac{m-1}{2m-1}\biggr] \chi Q_{m- 3 / 2}(\chi) - \biggl[ \frac{2m-3}{2m-1}\biggr] Q_{m- 5 / 2}(\chi) \, .</math> Excerpt from p. 490 of W. Guatschi (1965, Communications of the ACM, 8, 488 - 492)

See Also

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation