Difference between revisions of "User:Tohline/SSC/Stability/InstabilityOnsetOverview"
(→Stability: Develop text for stability subsection) |
|||
| Line 79: | Line 79: | ||
===Stability=== | ===Stability=== | ||
For any individual model along the equilibrium sequences depicted in Figure 1 — more specifically, for any choice of the truncation radius, <math>~\xi_e</math> — we can call upon traditional radial pulsation theory to determine the eigenvectors associated with that configuration's natural modes of radial oscillation. The determination of an eigenvector for a particular mode in a particular equilibrium model requires the simultaneous determination of how the fractional displacement, <math>~x \equiv \delta r/r</math>, varies with radial location throughout the configuration <math>~(0 < \xi \le \xi_e)</math>, and the associated frequency of oscillation, <math>~\omega</math>, of that mode. Formally, this is accomplished by solving the eigenvalue problem that is defined mathematically by the, | For any individual model along the equilibrium sequences depicted in Figure 1 — more specifically, for any choice of the truncation radius, <math>~\xi_e</math> — we can call upon traditional radial pulsation theory to determine the eigenvectors associated with that configuration's natural modes of radial oscillation. The determination of an eigenvector for a particular mode in a particular equilibrium model requires the simultaneous determination of how the fractional displacement, <math>~x \equiv \delta r/r</math>, varies with radial location throughout the configuration <math>~(0 < \xi \le \xi_e)</math>, and the associated (square of the) frequency of oscillation, <math>~\sigma_c^2 \equiv 3\omega^2/(2\pi G\rho_c)</math>, of that mode. Formally, in the context of pressure-truncated isothermal spheres, this is accomplished by solving the eigenvalue problem that is defined mathematically by the, | ||
<div align="center" id="IsothermalLAWE"> | <div align="center" id="IsothermalLAWE"> | ||
| Line 86: | Line 86: | ||
</div> | </div> | ||
When pursuing this type of analysis, it is broadly appreciated that a ''stable'' mode of radial oscillation will exhibit an eigenvector | subject to the boundary conditions, | ||
In an [[User:Tohline/SSC/Stability/Isothermal#From_the_Analysis_of_Taff_and_Van_Horn_.281974.29|accompanying discussion]], we review and replicate many aspects of the analysis presented by [http://adsabs.harvard.edu/abs/1974MNRAS.168..427T Taff & Van Horn (1974)] of radial modes of oscillation in pressure-truncated isothermal spheres. While focusing specifically on the ''fundamental'' mode of oscillation, Taff and Van Horn showed — as had [http://adsabs.harvard.edu/abs/1968MNRAS.140..109Y Yabushita (1968)] before them — that | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{dx}{d\xi} = 0</math> at <math>~\xi = 0</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{d\ln x}{d\ln\xi} = -3</math> at <math>~\xi = \xi_e</math>. | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
When pursuing this type of analysis, it is broadly appreciated that a ''stable'' mode of radial oscillation will exhibit an eigenvector with a ''positive'' value of <math>~\sigma_c^2</math>, while an eigenvector for which <math>~\sigma_c^2</math> is ''negative'' identifies a ''dynamically unstable'' mode of oscillation. | |||
In an [[User:Tohline/SSC/Stability/Isothermal#From_the_Analysis_of_Taff_and_Van_Horn_.281974.29|accompanying discussion]], we review and replicate many aspects of the computational analysis presented by [http://adsabs.harvard.edu/abs/1974MNRAS.168..427T Taff & Van Horn (1974)] of radial modes of oscillation in pressure-truncated isothermal spheres. They restricted their analysis to models having <math>~2 \le \xi_e \le 10</math>, that is, to models in the vicinity of the <math>~P_e</math>-max turning point; see the left panel of our Figure 1, above. While focusing specifically on the ''fundamental'' mode of oscillation, Taff and Van Horn showed — as had [http://adsabs.harvard.edu/abs/1968MNRAS.140..109Y Yabushita (1968)] before them — that <math>~\sigma_c^2</math> is positive for configurations that lie to the right of the <math>~P_e</math>-max turning point, while it is negative for configurations that lie to the right of this turning point. This result supported the astrophysics community's widely held expectation that the <math>~P_e</math>-max turning point is associated with the onset of a dynamical instability in pressure-truncated isothermal spheres. | |||
Yabushita ([http://adsabs.harvard.edu/abs/1974MNRAS.167…95Y 1974], [http://adsabs.harvard.edu/abs/1975MNRAS.172..441Y 1975]) showed that, if the adiabatic exponent is assigned the value, <math>~\gamma_g = 1</math>, in which case the parameter, <math>~\alpha = -1</math> | In a pair of papers that, to date, have not been widely cited, Yabushita ([http://adsabs.harvard.edu/abs/1974MNRAS.167…95Y 1974], [http://adsabs.harvard.edu/abs/1975MNRAS.172..441Y 1975]) provided solid ''proof'' that the <math>~P_e</math>-max turning point precisely marks the onset of dynamical instability in pressure-truncated isothermal spheres. Specifically, he showed that, if the adiabatic exponent is assigned the value, <math>~\gamma_g = 1</math>, in which case the parameter, <math>~\alpha = -1</math>, the following analytically defined eigenvector provides an | ||
the following analytically defined eigenvector provides | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="center" colspan="3"><font color="maroon"><b> | <td align="center" colspan="3"><font color="maroon"><b>Exact Solution to the Isothermal LAWE</b></font></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| Line 104: | Line 122: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, | <math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
In an [[User:Tohline/SSC/Stability/Isothermal#Yabushita_.281975.29|accompanying discussion]], we have demonstrated explicitly that this eigenvector is a solution to the isothermal LAWE. Along the way, we have also shown that the first logarithmic derivative of Yabushita's eigenfunction is given by the expression, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ - \frac{d\ln x}{d\ln\xi} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{x}\biggl[ (\psi ')^2 e^\psi + 3x-2\biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, if at the surface we impose a boundary condition, <math>~d\ln x/d\ln\xi = -3</math>, then this also means that, at the surface, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 115: | Line 152: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\biggl[ (\psi ')^2 e^\psi \biggr]_{\xi_e} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 121: | Line 158: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~2 \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
And this is precisely the condition, highlighted above, that Bonnor showed was associated with the critical <math>~P_e</math>-max turning point along the equilibrium sequence. Hence, as [http://adsabs.harvard.edu/abs/1975MNRAS.172..441Y Yabushita (1975)] recognized, we can precisely associate the configuration at the turning point with the marginally (dynamically) unstable configuration — that is, the one for which <math>~\sigma_c^2 = 0</math>. | |||
==Polytropic== | ==Polytropic== | ||
Revision as of 22:37, 21 March 2017
Overview: Marginally Unstable Pressure-Truncated Configurations
Additional details may be found here.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Isothermal
Structure
Once a central density, <math>~\rho_c</math>, and constituent fluid sound speed, <math>~c_s</math>, have been specified, the internal structure of an equilibrium, isothermal sphere can be completely described in terms of the function, <math>~\psi(\xi) \equiv \ln(\rho_c/\rho)</math>, which is a solution of the,
Isothermal Lane-Emden Equation
|
subject to the boundary conditions, <math>~ \psi = 0</math> and <math>~d\psi/d\xi = 0</math> at <math>~\xi = 0</math>. In isolation, the isothermal sphere extends to infinity. But configurations of finite extent can be constructed by truncating the function, <math>~\psi</math>, at some radius, <math>~0 < \xi_e < \infty</math> — such that the surface density is finite and set by the value of <math>~\psi_e \equiv \psi(\xi_e)</math> — and embedding the configuration in a hot, tenuous medium that exerts an "external" pressure, <math>~P_e = c_s^2 \rho_c e^{-\psi_e}</math>, uniformly across the surface of the — now, truncated — sphere. The internal structure of such a "pressure-truncated" isothermal sphere is completely describable in terms of the same function, <math>~\psi(\xi)</math>, that describes the structure of the isolated isothermal sphere, except that beyond <math>~\xi_e</math> the function becomes irrelevant.
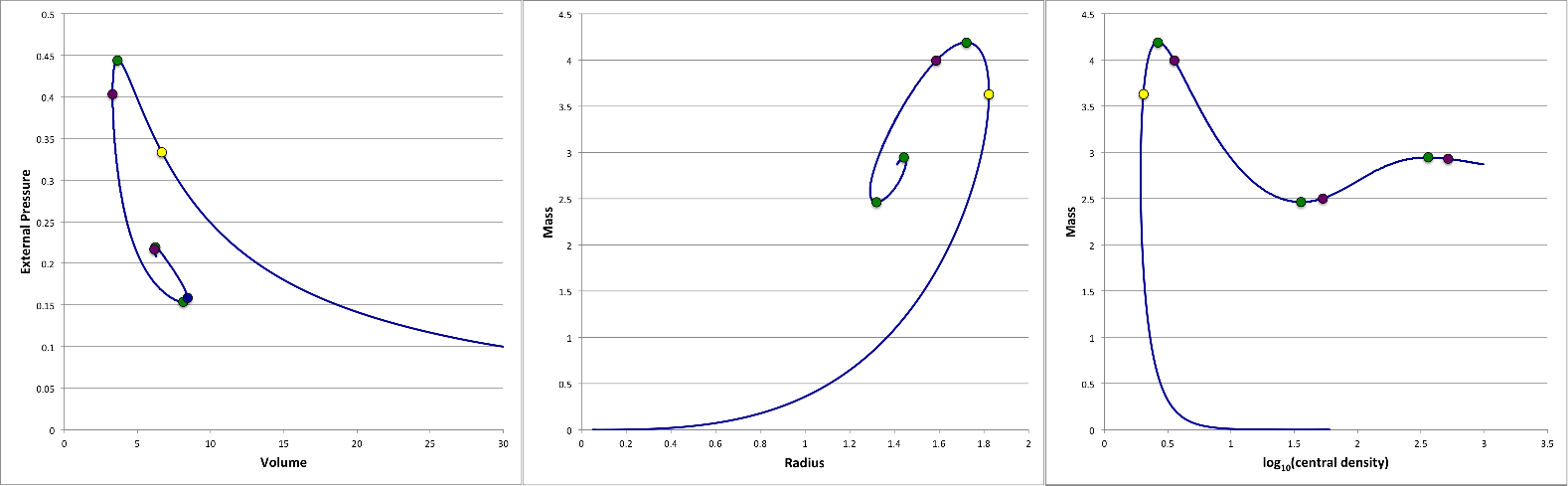
A sequence of equilibrium, pressure-truncated isothermal spheres is readily defined by varying the value of <math>~\xi_e</math>. Figure 1 displays the behavior of such an equilibrium sequence, as viewed from three different astrophysical perspectives (in all cases, <math>~c_s</math> is held fixed while <math>~\xi_e</math> is varied monotonically along the sequence): Left panel — A diagram showing how the truncated configuration's equilibrium volume varies with the externally applied pressure, if the configuration's mass is held fixed. Center panel — A diagram showing how the truncated configuration's mass varies with the equilibrium radius, if the external pressure is held fixed. Right panel — A diagram that shows how the configuration's mass varies with central density, if the external pressure is held fixed.
|
Figure 1: Equilibrium Sequences of Pressure-Truncated Isothermal Spheres |
||||
| ● | <math>~\xi_e</math> | †External Pressure vs. Volume (Fixed Mass) |
Mass vs. Radius (Fixed External Pressure) |
‡Mass vs. Central Density (Fixed External Pressure) |
| ● | 4.05 | |||
| ● | 6.45 | |||
| ● | 9.00 | |||
| ● | 67.00 | |||
| ● | 98.50 | |||
| ● | 735.00 | |||
| ● | 1060.00 | |||
|
†This is the classic P-V diagram that shows up in most discussions of Bonnor-Ebert spheres. |
||||
In Figure 1, the small, yellow circular marker identifies the configuration along each equilibrium sequence for which <math>~\xi_e = 4.05</math>. In the center panel it marks the approximate location of a "turning point" along the mass-radius equilibrium sequence; specifically, it identifies the configuration along the sequence that exhibits the maximum equilibrium radius. This yellow marker does not appear to be associated with any particularly special feature of the equilibrium sequence displayed in the left figure panel or the one displayed in the panel on the right. Moving along each of the displayed sequences, past the yellow marker, one encounters a small, green circular marker that identifies the configuration for which <math>~\xi_e = 6.45</math>. In the left panel, it marks the approximate location of another "turning point"; specifically, the turning point that identifies the external pressure above which no equilibrium configurations exist. It is clear that, in both the center panel and the right panel, this green marker is also associated with a turning point — the so-called Bonnor-Ebert limiting mass.
As we have reviewed in a separate chapter, Bonnor was the first to point out, in the context of the <math>~P-V</math> diagram (left panel of Figure 1), that the precise location of the turning point that is associated with the limiting pressure is given by the configuration for which,
<math>~\biggl[e^{\psi} \biggl( \frac{d\psi}{d\xi}\biggr)^2\biggr]_{\xi_e} = 2 \, .</math>
We have determined numerically that this condition is satisfied for <math>~\xi_e \approx 6.451053</math>.
Moving still further along each Figure 1 equilibrium sequence, one encounters in succession: a purple marker <math>~(\xi_e = 9)</math>; a green marker <math>~(\xi_e = 67)</math>; a purple marker <math>~(\xi_e = 98.5)</math>; a green marker <math>~(\xi_e = 735)</math>; and, finally, a purple marker <math>~(\xi_e = 1060)</math>. The two additional green markers were specifically put in place in the left panel of Figure 1 to identify the approximate locations of additional local extrema in the external pressure; and the three purple markers were put in place to identify the approximate locations of local extrema in the configuration volume. We see from the center and right panels that the configurations identified by the green markers are also associated with additional local extrema in the mass, but the purple markers do not appear to be associated with any particularly special feature of these two equilibrium sequences.
Stability
For any individual model along the equilibrium sequences depicted in Figure 1 — more specifically, for any choice of the truncation radius, <math>~\xi_e</math> — we can call upon traditional radial pulsation theory to determine the eigenvectors associated with that configuration's natural modes of radial oscillation. The determination of an eigenvector for a particular mode in a particular equilibrium model requires the simultaneous determination of how the fractional displacement, <math>~x \equiv \delta r/r</math>, varies with radial location throughout the configuration <math>~(0 < \xi \le \xi_e)</math>, and the associated (square of the) frequency of oscillation, <math>~\sigma_c^2 \equiv 3\omega^2/(2\pi G\rho_c)</math>, of that mode. Formally, in the context of pressure-truncated isothermal spheres, this is accomplished by solving the eigenvalue problem that is defined mathematically by the,
Isothermal LAWE (linear adiabatic wave equation)
|
<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math> |
|
|
where: <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math> and, <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math> |
|
subject to the boundary conditions,
|
<math>~\frac{dx}{d\xi} = 0</math> at <math>~\xi = 0</math> |
and |
<math>~\frac{d\ln x}{d\ln\xi} = -3</math> at <math>~\xi = \xi_e</math>. |
When pursuing this type of analysis, it is broadly appreciated that a stable mode of radial oscillation will exhibit an eigenvector with a positive value of <math>~\sigma_c^2</math>, while an eigenvector for which <math>~\sigma_c^2</math> is negative identifies a dynamically unstable mode of oscillation.
In an accompanying discussion, we review and replicate many aspects of the computational analysis presented by Taff & Van Horn (1974) of radial modes of oscillation in pressure-truncated isothermal spheres. They restricted their analysis to models having <math>~2 \le \xi_e \le 10</math>, that is, to models in the vicinity of the <math>~P_e</math>-max turning point; see the left panel of our Figure 1, above. While focusing specifically on the fundamental mode of oscillation, Taff and Van Horn showed — as had Yabushita (1968) before them — that <math>~\sigma_c^2</math> is positive for configurations that lie to the right of the <math>~P_e</math>-max turning point, while it is negative for configurations that lie to the right of this turning point. This result supported the astrophysics community's widely held expectation that the <math>~P_e</math>-max turning point is associated with the onset of a dynamical instability in pressure-truncated isothermal spheres.
In a pair of papers that, to date, have not been widely cited, Yabushita (1974, 1975) provided solid proof that the <math>~P_e</math>-max turning point precisely marks the onset of dynamical instability in pressure-truncated isothermal spheres. Specifically, he showed that, if the adiabatic exponent is assigned the value, <math>~\gamma_g = 1</math>, in which case the parameter, <math>~\alpha = -1</math>, the following analytically defined eigenvector provides an
| Exact Solution to the Isothermal LAWE | ||
|
<math>~\sigma_c^2 = 0</math> |
and |
<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, .</math> |
In an accompanying discussion, we have demonstrated explicitly that this eigenvector is a solution to the isothermal LAWE. Along the way, we have also shown that the first logarithmic derivative of Yabushita's eigenfunction is given by the expression,
|
<math>~ - \frac{d\ln x}{d\ln\xi} </math> |
<math>~=</math> |
<math>~\frac{1}{x}\biggl[ (\psi ')^2 e^\psi + 3x-2\biggr] \, .</math> |
Hence, if at the surface we impose a boundary condition, <math>~d\ln x/d\ln\xi = -3</math>, then this also means that, at the surface,
|
<math>~\biggl[ (\psi ')^2 e^\psi \biggr]_{\xi_e} </math> |
<math>~=</math> |
<math>~2 \, .</math> |
And this is precisely the condition, highlighted above, that Bonnor showed was associated with the critical <math>~P_e</math>-max turning point along the equilibrium sequence. Hence, as Yabushita (1975) recognized, we can precisely associate the configuration at the turning point with the marginally (dynamically) unstable configuration — that is, the one for which <math>~\sigma_c^2 = 0</math>.
Polytropic
Given a value of the polytropic index, <math>~n</math>, the internal structure of a detailed force-balance model is provided via the function, <math>~\theta(\xi)</math>, which is a solution of the,
Polytropic Lane-Emden Equation
|
subject to the boundary conditions, <math>~\Theta_H = 1</math> and <math>~d\Theta_H/d\xi = 0</math> at <math>~\xi = 0</math>.
To identify pure radial oscillation modes, we seek solutions to the,
Polytropic LAWE
|
<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math> |
|
|
where: <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math> <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math> and, <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math> |
|
We have discovered that, for any value of the polytropic index in the range, <math>~3 \le n < \infty</math>, the following eigenvector specification provides a
| ||||||
if the adiabatic exponent is assigned the value, <math>~\gamma_g = (n+1)/n</math>, in which case the parameter, <math>~\alpha = (3-n)/(n+1)</math>.
References

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |