Difference between revisions of "User:Tohline/SSC/Stability/InstabilityOnsetOverview"
| Line 18: | Line 18: | ||
subject to the boundary conditions, <math>~ \psi = 0</math> and <math>~d\psi/d\xi = 0</math> at <math>~\xi = 0</math>. In isolation, the isothermal sphere extends to infinity. But configurations of finite extent can be constructed by truncating the function, <math>~\psi</math>, at some radius, <math>~0 < \xi_e < \infty</math> — such that the surface density is finite and set by the value of <math>~\psi_e \equiv \psi(\xi_e)</math> — and embedding the configuration in a hot, tenuous medium that exerts an "external" pressure, <math>~P_e = c_s^2 \rho_c e^{-\psi_e}</math>, uniformly across the surface of the — now, truncated — sphere. The internal structure of such a "pressure-truncated" isothermal sphere is completely describable in terms of the same function, <math>~\psi(\xi)</math>, that describes the structure of the isolated isothermal sphere, except that beyond <math>~\xi_e</math> the function becomes irrelevant. | subject to the boundary conditions, <math>~ \psi = 0</math> and <math>~d\psi/d\xi = 0</math> at <math>~\xi = 0</math>. In isolation, the isothermal sphere extends to infinity. But configurations of finite extent can be constructed by truncating the function, <math>~\psi</math>, at some radius, <math>~0 < \xi_e < \infty</math> — such that the surface density is finite and set by the value of <math>~\psi_e \equiv \psi(\xi_e)</math> — and embedding the configuration in a hot, tenuous medium that exerts an "external" pressure, <math>~P_e = c_s^2 \rho_c e^{-\psi_e}</math>, uniformly across the surface of the — now, truncated — sphere. The internal structure of such a "pressure-truncated" isothermal sphere is completely describable in terms of the same function, <math>~\psi(\xi)</math>, that describes the structure of the isolated isothermal sphere, except that beyond <math>~\xi_e</math> the function becomes irrelevant. | ||
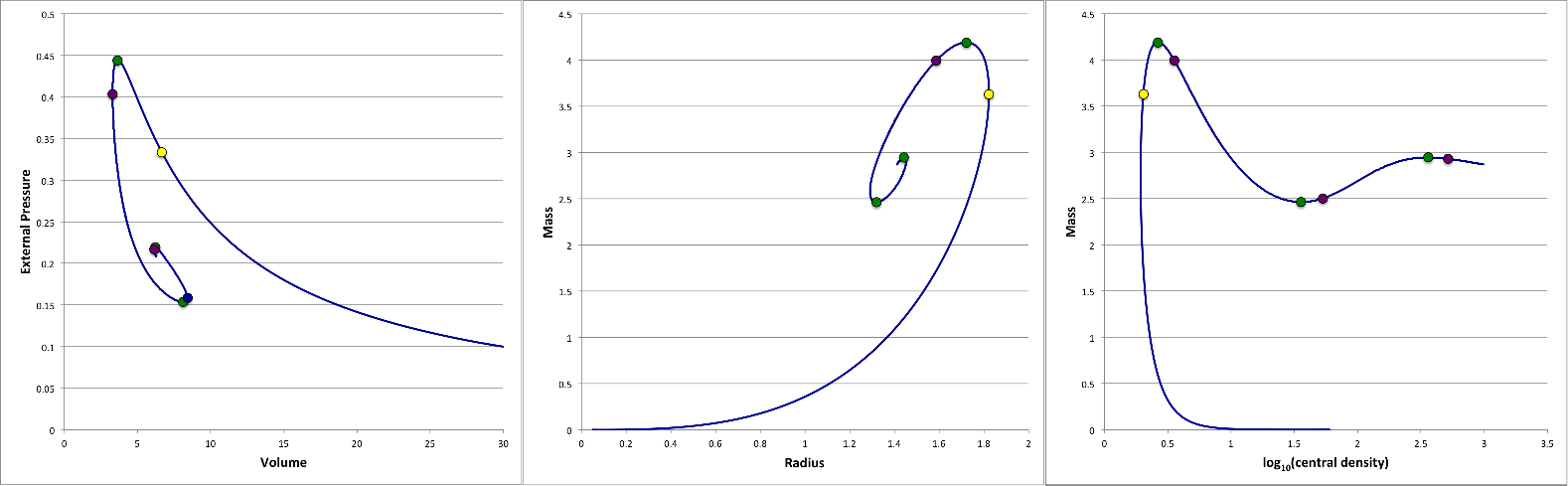
A ''sequence'' of equilibrium, pressure-truncated isothermal spheres is readily defined by varying the value of <math>~\xi_e</math>. Figure 1 displays the behavior of such an equilibrium sequence, as viewed from three different astrophysical perspectives (in all cases, <math>~c_s</math> is held fixed while <math>~\xi_e</math> is varied monotonically along the sequence): ''Left panel'' — A | A ''sequence'' of equilibrium, pressure-truncated isothermal spheres is readily defined by varying the value of <math>~\xi_e</math>. Figure 1 displays the behavior of such an equilibrium sequence, as viewed from three different astrophysical perspectives (in all cases, <math>~c_s</math> is held fixed while <math>~\xi_e</math> is varied monotonically along the sequence): ''Left panel'' — A diagram showing how the truncated configuration's equilibrium volume varies with the externally applied pressure, if the configuration's mass is held fixed. ''Center panel'' — A diagram showing how the truncated configuration's mass varies with the equilibrium radius, if the external pressure is held fixed. ''Right panel'' — A diagram that shows how the configuration's mass varies with central density, if the external pressure is held fixed. | ||
<div align="center"> | <div align="center"> | ||
| Line 60: | Line 60: | ||
<td align="left" colspan="5"> | <td align="left" colspan="5"> | ||
<sup>†</sup>This is the classic P-V diagram that shows up in most discussions of [[User:Tohline/SSC/Structure/BonnorEbert#Fig1|Bonnor-Ebert spheres]].<br /> | <sup>†</sup>This is the classic P-V diagram that shows up in most discussions of [[User:Tohline/SSC/Structure/BonnorEbert#Fig1|Bonnor-Ebert spheres]].<br /> | ||
<sup>‡</sup>In a similar diagram in which the radius | <sup>‡</sup>In a similar diagram in which the radius (rather than external pressure) is held fixed, the purple (rather than green) markers identify mass extrema. | ||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 18:02, 20 March 2017
Overview: Marginally Unstable Pressure-Truncated Configurations
Additional details may be found here.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Isothermal
Once a central density, <math>~\rho_c</math>, and constituent fluid sound speed, <math>~c_s</math>, have been specified, the internal structure of an equilibrium, isothermal sphere can be completely described in terms of the function, <math>~\psi(\xi) \equiv \ln(\rho_c/\rho)</math>, which is a solution of the,
Isothermal Lane-Emden Equation
|
subject to the boundary conditions, <math>~ \psi = 0</math> and <math>~d\psi/d\xi = 0</math> at <math>~\xi = 0</math>. In isolation, the isothermal sphere extends to infinity. But configurations of finite extent can be constructed by truncating the function, <math>~\psi</math>, at some radius, <math>~0 < \xi_e < \infty</math> — such that the surface density is finite and set by the value of <math>~\psi_e \equiv \psi(\xi_e)</math> — and embedding the configuration in a hot, tenuous medium that exerts an "external" pressure, <math>~P_e = c_s^2 \rho_c e^{-\psi_e}</math>, uniformly across the surface of the — now, truncated — sphere. The internal structure of such a "pressure-truncated" isothermal sphere is completely describable in terms of the same function, <math>~\psi(\xi)</math>, that describes the structure of the isolated isothermal sphere, except that beyond <math>~\xi_e</math> the function becomes irrelevant.
A sequence of equilibrium, pressure-truncated isothermal spheres is readily defined by varying the value of <math>~\xi_e</math>. Figure 1 displays the behavior of such an equilibrium sequence, as viewed from three different astrophysical perspectives (in all cases, <math>~c_s</math> is held fixed while <math>~\xi_e</math> is varied monotonically along the sequence): Left panel — A diagram showing how the truncated configuration's equilibrium volume varies with the externally applied pressure, if the configuration's mass is held fixed. Center panel — A diagram showing how the truncated configuration's mass varies with the equilibrium radius, if the external pressure is held fixed. Right panel — A diagram that shows how the configuration's mass varies with central density, if the external pressure is held fixed.
|
Figure 1: Equilibrium Sequences of Pressure-Truncated Isothermal Spheres |
||||
| ● | <math>~\xi_e</math> | †External Pressure vs. Volume (Fixed Mass) |
Mass vs. Radius (Fixed External Pressure) |
‡Mass vs. Central Density (Fixed External Pressure) |
| ● | 4.05 | |||
| ● | 6.45 | |||
| ● | 9.00 | |||
| ● | 67.00 | |||
| ● | 98.50 | |||
| ● | 735.00 | |||
| ● | 1060.00 | |||
|
†This is the classic P-V diagram that shows up in most discussions of Bonnor-Ebert spheres. |
||||
This equation — in the following, slightly rewritten form — can be found among our selected set of key equations associated with the study of radial pulsation, and will henceforth be referred to as the,
Isothermal LAWE
|
<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math> |
|
|
where: <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math> and, <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math> |
|
Yabushita (1974, 1975) showed that the following eigenvector specification provides a
| Precise Solution to the Isothermal LAWE | ||
|
<math>~\sigma_c^2 = 0</math> |
and |
<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, ,</math> |
if the adiabatic exponent is assigned the value, <math>~\gamma_g = 1</math>, in which case the parameter, <math>~\alpha = -1</math>. When viewed in concert with the surface boundary condition,
|
<math>~\frac{d\ln x}{d\ln\xi}</math> |
<math>~=</math> |
<math>~- 3 \, ,</math> |
the relevant configuration is precisely defined by the surface condition, xxx, which is identical to the configuration at the turning point.
Polytropic
Given a value of the polytropic index, <math>~n</math>, the internal structure of a detailed force-balance model is provided via the function, <math>~\theta(\xi)</math>, which is a solution of the,
Polytropic Lane-Emden Equation
|
subject to the boundary conditions, <math>~\Theta_H = 1</math> and <math>~d\Theta_H/d\xi = 0</math> at <math>~\xi = 0</math>.
To identify pure radial oscillation modes, we seek solutions to the,
Polytropic LAWE
|
<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math> |
|
|
where: <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math> <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math> and, <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math> |
|
We have discovered that, for any value of the polytropic index in the range, <math>~3 \le n < \infty</math>, the following eigenvector specification provides a
| ||||||
if the adiabatic exponent is assigned the value, <math>~\gamma_g = (n+1)/n</math>, in which case the parameter, <math>~\alpha = (3-n)/(n+1)</math>.
References

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |