User:Tohline/SSC/Stability/InstabilityOnsetOverview

Overview: Marginally Unstable Pressure-Truncated Configurations

Additional details may be found here.

Isothermal

Once a central density, <math>~\rho_c</math>, and constituent fluid sound speed, <math>~c_s</math>, have been specified, the internal structure of an equilibrium, isothermal sphere can be completely described in terms of the function, <math>~\psi(\xi) \equiv \ln(\rho_c/\rho)</math>, which is a solution of the,

Isothermal Lane-Emden Equation <math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\psi}{d\xi} \biggr) = e^{-\psi}</math>

subject to the boundary conditions, <math>~ \psi = 0</math> and <math>~d\psi/d\xi = 0</math> at <math>~\xi = 0</math>. In isolation, the isothermal sphere extends to infinity. But configurations of finite extent can be constructed by truncating the function, <math>~\psi</math>, at some radius, <math>~0 < \xi_e < \infty</math> — such that the surface density is finite and set by the value of <math>~\psi_e \equiv \psi(\xi_e)</math> — and embedding the configuration in a hot, tenuous medium that exerts an "external" pressure, <math>~P_e = c_s^2 \rho_c e^{-\psi_e}</math>, uniformly across the surface of the — now, truncated — sphere. The internal structure of such a "pressure-truncated" isothermal sphere is completely describable in terms of the same function, <math>~\psi(\xi)</math>, that describes the structure of the isolated isothermal sphere, except that beyond <math>~\xi_e</math> the function becomes irrelevant.

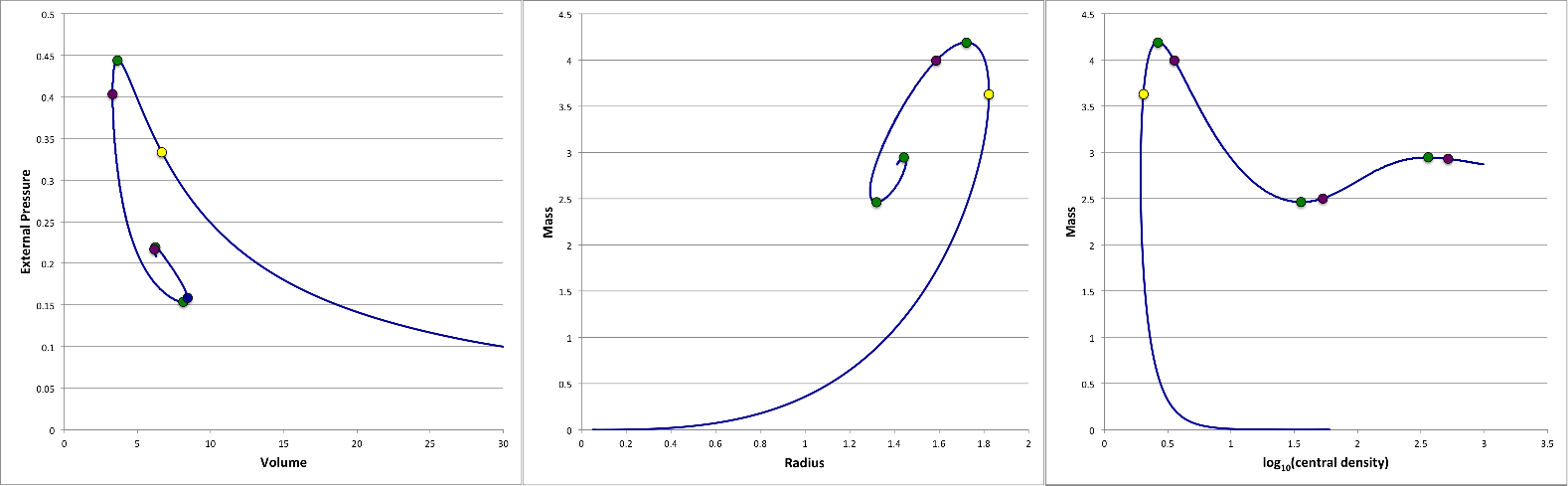
A sequence of equilibrium, pressure-truncated isothermal spheres is readily defined by varying the value of <math>~\xi_e</math>. Figure 1 displays the behavior of such an equilibrium sequence, as viewed from three different astrophysical perspectives (in all cases, <math>~c_s</math> is held fixed while <math>~\xi_e</math> is varied monotonically along the sequence):   Left panel — A pressure-volume diagram, which shows how the truncated configuration's equilibrium volume varies with the externally applied pressure, if the configuration's mass is held fixed. Center panel — A mass-radius diagram, which shows how the truncated configuration's mass varies with the equilibrium radius, if the external pressure is held fixed. Right panel — A diagram that shows how the configuration's mass varies with central density, if the external pressure is held fixed.

Figure 1:   Equilibrium Sequences of Pressure-Truncated Isothermal Spheres (viewed from three different astrophysical perspectives)
●	<math>~\xi_e</math>	†External Pressure vs. Volume (Fixed Mass)	Mass vs. Radius (Fixed External Pressure)	‡Mass vs. Central Density (Fixed External Pressure)
●	4.05
●	6.45
●	9.00
●	67.00
●	98.50
●	735.00
●	1060.00
†This is the classic P-V diagram that shows up in most discussions of Bonnor-Ebert spheres. ‡In a similar diagram in which the radius, rather than external pressure, is held fixed, the purple (rather than green) markers identify mass extrema.

This equation — in the following, slightly rewritten form — can be found among our selected set of key equations associated with the study of radial pulsation, and will henceforth be referred to as the,

Isothermal LAWE

	<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math>
where:    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

Yabushita (1974, 1975) showed that the following eigenvector specification provides a

Precise Solution to the Isothermal LAWE
<math>~\sigma_c^2 = 0</math>	and	<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} \, ,</math>

if the adiabatic exponent is assigned the value, <math>~\gamma_g = 1</math>, in which case the parameter, <math>~\alpha = -1</math>. When viewed in concert with the surface boundary condition,

<math>~\frac{d\ln x}{d\ln\xi}</math>

<math>~=</math>

<math>~- 3 \, ,</math>

the relevant configuration is precisely defined by the surface condition, xxx, which is identical to the configuration at the turning point.

Polytropic

Given a value of the polytropic index, <math>~n</math>, the internal structure of a detailed force-balance model is provided via the function, <math>~\theta(\xi)</math>, which is a solution of the,

Polytropic Lane-Emden Equation <math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math>

subject to the boundary conditions, <math>~\Theta_H = 1</math> and <math>~d\Theta_H/d\xi = 0</math> at <math>~\xi = 0</math>.

To identify pure radial oscillation modes, we seek solutions to the,

Polytropic LAWE

	<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math>
where:    <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math>    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

We have discovered that, for any value of the polytropic index in the range, <math>~3 \le n < \infty</math>, the following eigenvector specification provides a

Precise Solution to the Polytropic LAWE <math>~\sigma_c^2 = 0</math>   and   <math>~x = 1 + \biggl(\frac{n-3}{n-1}\biggr) \biggl( \frac{1}{\xi \theta^{n}}\biggr) \frac{d\theta}{d\xi} </math>

if the adiabatic exponent is assigned the value, <math>~\gamma_g = (n+1)/n</math>, in which case the parameter, <math>~\alpha = (3-n)/(n+1)</math>.

References

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation