Difference between revisions of "User:Tohline/Appendix/Ramblings/NumericallyDeterminedEigenvectors"
(Begin new "Ramblings" chapter) |
|||
| (49 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
==Setup== | |||
We'll begin with the linear-adiabatic wave equations that describe oscillations of the core and envelope, separately. We also will immediately restrict our investigation to configurations for which, | We'll begin with the linear-adiabatic wave equations that describe oscillations of the core and envelope, separately. We also will immediately restrict our investigation to configurations for which, | ||
<div align="center"> | <div align="center"> | ||
| Line 33: | Line 34: | ||
(1 - \eta^2)\frac{d^2x}{d\eta^2} + | (1 - \eta^2)\frac{d^2x}{d\eta^2} + | ||
( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx}{d\eta} | ( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx}{d\eta} | ||
+ \mathfrak{F}_\mathrm{core} x \, | + \mathfrak{F}_\mathrm{core} x \, , | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 59: | Line 60: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | ( 1 - q^3 \xi^3 ) \frac{d^2x}{d\xi^2} + ( 3 - 6q^3 \xi^3 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} | ||
+ | |||
\frac{ | \biggl[ q^3 \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e | ||
+ \biggl | \biggr]\frac{x}{\xi^2} \, , | ||
\ | </math> | ||
\ | </td> | ||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F}_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3\omega^2_\mathrm{env}}{2\pi G \gamma_e \rho_e} - 2\alpha_e | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<!-- THIS SHOWS HOW THE ABOVE LAWE WAS DERIVED ... | |||
For the [[User:Tohline/SSC/Stability/BiPolytrope0_0Details#EnvelopeLAWE|envelope]] we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \mathcal{A} + (g^2-\mathcal{B}) \xi - \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3\biggr] \biggl[ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} \biggr] | |||
+ \biggl\{ 3\mathcal{A} + 4(g^2-\mathcal{B}) \xi - 6\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3 \biggr\} | |||
\frac{\xi}{x} \cdot \frac{dx}{d\xi} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 74: | Line 116: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | + \biggl[ | ||
\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl( \mathfrak{F} + 2\alpha -2\alpha\frac{\rho_e}{\rho_c} \biggr)\xi^3 -\alpha \mathcal{A} | |||
\ | \biggr] \, , | ||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 99: | Line 140: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) | <math>~2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) = \frac{4q^3}{(1+2q^3)^2} ~~\Rightarrow ~~~ \frac{1}{\mathcal{A}}\biggl( \frac{\rho_e}{\rho_c}\biggr)^2 = q^3 \, ; | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 113: | Line 154: | ||
<td align="left"> | <td align="left"> | ||
<math>~1 + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) - 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 | <math>~1 + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) - 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 | ||
\, , | \, . | ||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Note, as well, that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F} + 2\alpha -2\alpha \biggl( \frac{\rho_e}{\rho_c}\biggr)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\rightarrow</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{\rho_e}{\rho_c}\biggr) \mathfrak{F}_\mathrm{env} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, the LAWE for the envelope becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1 + \frac{ (g^2-\mathcal{B}) \xi}{\mathcal{A}} - \frac{1}{\mathcal{A}}\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3\biggr] \biggl[ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} \biggr] | |||
+ \biggl\{ 3 + \frac{ 4(g^2-\mathcal{B}) \xi }{\mathcal{A}} - \frac{6}{\mathcal{A}} \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \xi^3 \biggr\} | |||
\frac{\xi}{x} \cdot \frac{dx}{d\xi} | |||
+ \biggl[ | |||
\frac{1}{\mathcal{A}} \biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
( 1 -q^3 \xi^3 ) \biggl[ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} \biggr] + ( 3 - 6q^3 \xi^3 ) \frac{\xi}{x} \cdot \frac{dx}{d\xi} | |||
+ \biggl[ q^3 \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
END OF DERIVATION --> | |||
==Initial Focus== | |||
===Properties of 21Analytic Solution=== | |||
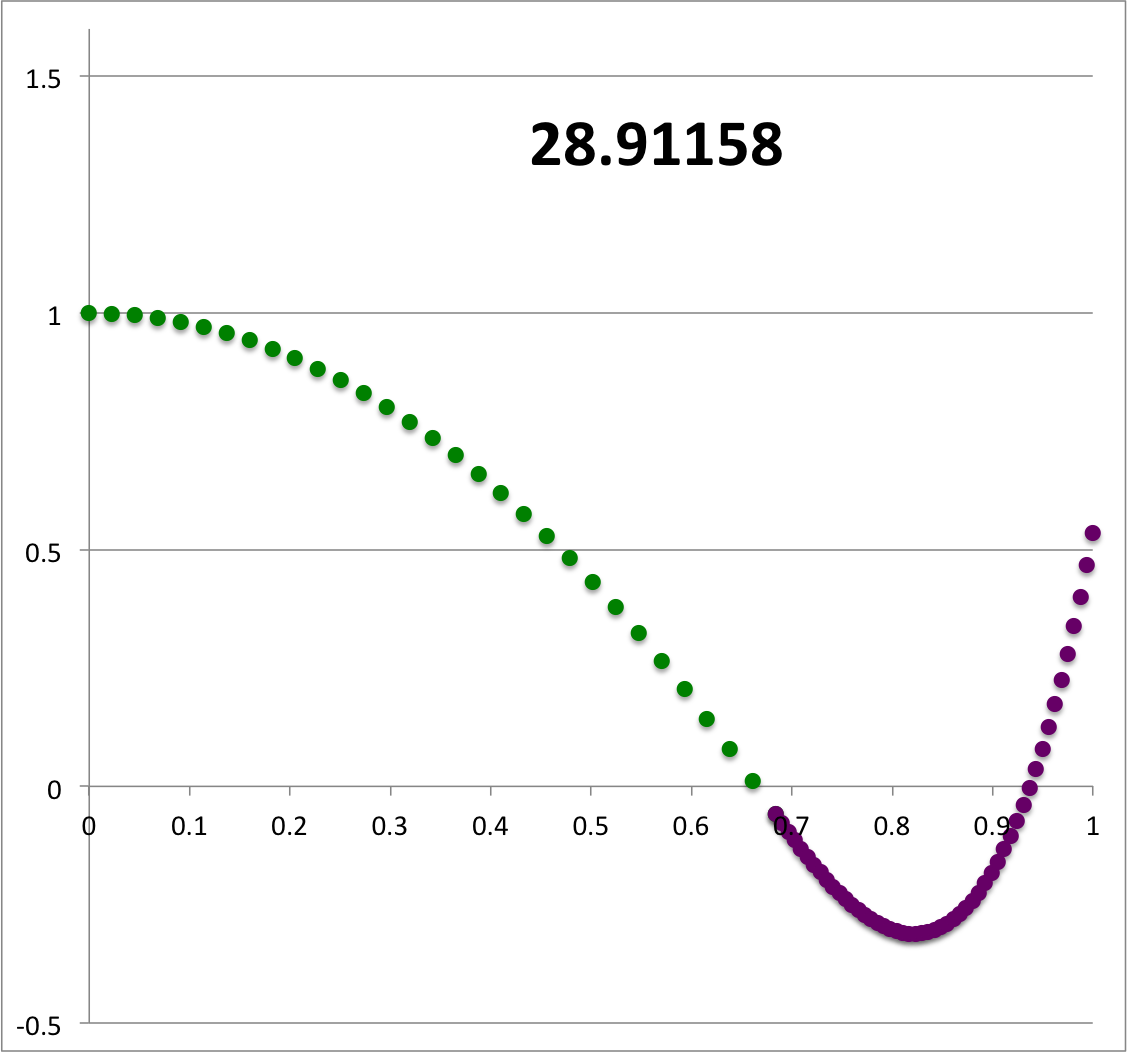
<span id="Figure1"><table border="1" align="right" width="320px" cellpadding="8"> | |||
<tr><th align="center">Figure 1</th></tr> | |||
<tr><td align="center"> | |||
[[File:ReferenceAnalyticSoln.png|300px|reference analytic solution]] | |||
</td></tr> | |||
<tr> | |||
<td align="left"> | |||
Same analytic, <math>~(\ell,j) = (2,1)</math> eigenfunction as [[User:Tohline/Appendix/Ramblings/Additional_Analytically_Specified_Eigenvectors_for_Zero-Zero_Bipolytropes#Illustration21|here]], but renormalized to unity at the center; numerical label provides value of <math>~\sigma_c^2</math>. | |||
</td> | |||
</tr> | |||
</table> | |||
</span> | |||
Evidently, [[User:Tohline/SSC/Stability/BiPolytrope0_0#Figure1|one analytic solution]] with quantum numbers, <math>~(\ell,j) = (2,1)</math>, shown again here on the right, is available for a zero-zero bipolytrope that has the following properties: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~q</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0.6840119</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\rho_e}{\rho_c} = \frac{2q^3}{1+2q^3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0.3902664</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\gamma_e = \frac{4}{3+0.35}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1.1940299</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\gamma_c </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1.845579</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G \rho_c} = 20\gamma_c - 8 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~28.91158 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This means, as well, that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~c_0 \equiv \sqrt{1+\alpha_e} - 1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\sqrt{0.65}-1 \approx - 0.1937742</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~g^2 \equiv \frac{1+8q^3}{(1+2q^3)^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1.3236092</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F}_\mathrm{core} \equiv \frac{\sigma_c^2 + 8}{\gamma_c} - 6</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~14</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F}_\mathrm{env} \equiv \frac{1}{\gamma_e} \biggl[ \sigma_c^2 \biggl(\frac{\rho_c}{\rho_e} \biggr) + 8\biggr]- 6</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(c_0^2 + 17c_0 +66) = 62.743385</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In the envelope, the analytically defined eigenfunction is given by the expression, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_{\ell=2} |_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\xi^{c_0}\biggl[ \frac{ 1 + q^3 A_{21} \xi^{3} + q^6 A_{21}B_{21}\xi^{6} }{ 1 + q^3 A_{21} + q^6 A_{21}B_{21}}\biggr] \, , | |||
</math> | </math> | ||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="3" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~A_{21}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-\biggl( \frac{ 4c_0 + 22}{2c_0 + 5}\biggr) \approx -4.6016533 \, ,</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 120: | Line 391: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~B_{21}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 126: | Line 397: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~-\biggl( \frac{c_0 + 7 }{2c_0+8}\biggr) \approx -0.8940912 \, ; </math> | ||
\, , | </td> | ||
</tr> | |||
</table> | |||
</div> | |||
and in the core, it is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_{j=1} |_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5(1+8q^3) - 7 (1+2q^3)^2 \xi^2}{5(1+8q^3)-7(1+2q^3)^2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
More succinctly we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-17.326820 + 18.326820~\xi^2 \, ;</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a \cdot x_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<math>~a \equiv -[ 1 + q^3 A_{21} + q^6 A_{21}B_{21}] \approx - 0.05128445 \, .</math> | |||
</div> | |||
===Demonstrate Core Solution=== | |||
This means that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{F}_\mathrm{ | <math>~\frac{dx_\mathrm{core}}{d\xi}</math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~36.65364~\xi \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d^2x_\mathrm{core}}{d\xi^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~36.65364 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Therefore, the LAWE for the core becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="left"> | |||
<math>~[\mathrm{LAWE}]_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(1 - \eta^2)\frac{d^2x_\mathrm{core}}{d\eta^2} + | |||
( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx_\mathrm{core}}{d\eta} | |||
+ \mathfrak{F}_\mathrm{core} x_\mathrm{core} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(g^2 - \xi^2)\frac{d^2x_\mathrm{core}}{d\xi^2} + | |||
( 4g^2 - 6\xi^2 ) \frac{1}{\xi} \cdot \frac{dx_\mathrm{core}}{d\xi} | |||
+ \mathfrak{F}_\mathrm{core} x_\mathrm{core} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
36.65364(1.3236092 - \xi^2) + | |||
36.65364( 5.2944368 - 6\xi^2 ) | |||
+ 14( -17.326820 + 18.326820~\xi^2) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
36.65364(1.3236092 ) + 36.65364( 5.2944368 ) + 14( -17.326820 ) | |||
+ [36.65364(-1) + 36.65364( - 6 ) + 14( 18.326820)]\xi^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
36.65364(6.618046 ) - 14( 17.326820 ) | |||
+ 36.65364 [-1 - 6 + 7]\xi^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\, . | 0 \, . | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 147: | Line 598: | ||
</table> | </table> | ||
</div> | </div> | ||
Q.E.D. | |||
===Demonstrate Envelope Solution=== | |||
Given that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 155: | Line 608: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~a\cdot x_\mathrm{env}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 161: | Line 614: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 167: | Line 622: | ||
</div> | </div> | ||
we deduce that, | |||
<div align="center"> | <div align="center"> | ||
<math>~ | <table border="0" cellpadding="5" align="center"> | ||
<math>~0 \ | <tr> | ||
<td align="right"> | |||
<math>~a\cdot \frac{dx_\mathrm{env}}{d\xi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-0.1937742~ | |||
\xi^{- 1.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
+ | |||
\xi^{- 0.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | and, | ||
| <div align="center"> | ||
<math>~0 \ | <table border="0" cellpadding="5" align="center"> | ||
<tr> | |||
<td align="right"> | |||
<math>~a \cdot \frac{d^2x_\mathrm{env}}{d\xi^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 0.2313226~ | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
- 2 \times 0.1937742~ | |||
\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
Therefore, the LAWE for the envelope becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a\cdot [\mathrm{LAWE}]_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
a( 1 - q^3 \xi^3 ) \frac{d^2x}{d\xi^2} + a( 3 - 6q^3 \xi^3 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} | |||
+ | |||
a\biggl[ q^3 \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e | |||
\biggr]\frac{x}{\xi^2} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{3}{\xi} \cdot \frac{dx}{d\xi} -\alpha_e \biggl(\frac{x}{\xi^2} \biggr) \biggr\} | |||
- a q^3 \xi^3 \biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} | |||
- \mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr)\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Now, the first of these sub-expressions gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{3}{\xi} \cdot \frac{dx}{d\xi} -\alpha_e \biggl(\frac{x}{\xi^2} \biggr) \biggr\} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 0.2313226~ | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
- 2 \times 0.1937742~ | |||
\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
== | <tr> | ||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-0.5813226~ | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
+ | |||
3\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~+0.35 | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ (0.2313226 -0.5813226 + 0.35) ~ | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
< | <tr> | ||
< | <td align="right"> | ||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ (3 - 2 \times 0.1937742)~ | |||
\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] | |||
+ \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
{{ | <tr> | ||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(3 - 2 \times 0.1937742)~ | |||
\xi^{- 2.1937742}\biggl[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} \biggr] | |||
+ \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\xi^{- 2.1937742}\biggl[ -20.37783~ \xi^3 + 19.24657~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
And the sub-expression inside the second set of curly braces gives, | |||
<div align="center" | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | |||
<math> | <tr> | ||
\frac{d^2x}{ | <td align="right"> | ||
<math>~ | |||
a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} -\mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr) \biggr\} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 0.2313226~ | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
- 2 \times 0.1937742~ | |||
\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-1.1626452~ | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
+ | |||
6\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~- 62.74339 | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ (0.2313226 -1.1626452 - 62.74339)~ | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ (6- 2 \times 0.1937742)~ | |||
\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] | |||
+ \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -63.67471~ | |||
\xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 5.612452~ | |||
\xi^{- 2.1937742}\biggl[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} \biggr] | |||
+ \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\xi^{- 2.1937742}\biggl[ -63.67471 + 93.77171~ \xi^{3} -26.83148~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ ~ | |||
\xi^{- 2.1937742}\biggl[ - 24.79584~ \xi^{3} + 14.18997~\xi^{6} \biggr] | |||
+ \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\xi^{- 2.1937742}\biggl[ -63.67471 + (93.77171-24.79584- 8.8360086) ~ \xi^{3} + (-26.83148+14.18997 + 12.641508)~\xi^{6} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\xi^{- 2.1937742}\biggl[ -63.67471 + 60.13986 ~ \xi^{3} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
a(q^3\xi^3) \biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} -\mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr) \biggr\} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\xi^{- 2.1937742}\biggl[ -20.37783 +19.24657 ~ \xi^{6} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
But these two sub-expressions cancel precisely, which means that our eigenfunction satisfies the LAWE! Q.E.D. | |||
===Boundary Conditions=== | |||
Notice that for this ''particular'' eigenfunction solution, the value and first radial derivative at the center <math>~(\xi=0)</math> of the configuration is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-17.326820 + 18.326820~\cancelto{0}{\xi^2} = -17.326820 \, ;</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{dx_\mathrm{core}}{d\xi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~36.65364~\cancelto{0}{\xi} = 0 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
And, at the surface <math>~(\xi = q^{-1}) </math> the value and first radial derivative are, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a \cdot x_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{\xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \biggr\}_{\xi=1/q} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
0.47627246\, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<math>~a \approx - 0.05128445 \, ;</math> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\ln x_\mathrm{env}}{d\ln \xi} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\xi}{a\cdot x_\mathrm{env}} \biggl[ a\cdot \frac{dx_\mathrm{env}}{d\xi} \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ -0.1937742~\xi^{- 0.1937742}[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] + \xi^{- 0.1937742}[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{\xi^{- 0.1937742} [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -0.1937742 + | |||
\frac{~ [ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{ [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl\{ \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr\}_{\xi=1/q} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -0.1937742 + \biggl\{ | |||
\frac{[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{ [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } \biggr\}_{\xi=1/q} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -0.1937742 + 21.22492 = 21.03115 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Finite-Difference Representation== | |||
===General Approach=== | |||
Working with the Taylor series expansion, we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x(\xi)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x(a) + (\xi - a) x_a' + \tfrac{1}{2} (\xi-a)^2 x_a'' \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and letting <math>~\xi_\pm = a \pm \Delta </math>, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_+</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x(a) + \Delta \cdot x_a' + \tfrac{1}{2} \Delta^2 x_a'' \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_-</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x(a) - \Delta \cdot x_a' + \tfrac{1}{2} \Delta^2 x_a'' \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Subtracting the second of these two expressions from the first gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_+ - x_-</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2 \Delta \cdot x_a' | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ x_a'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{x_+ - x_-}{2 \Delta} \, ; | |||
</math> | </math> | ||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
while, adding the two expressions together gives, | |||
<div align="center"> | <div align="center"> | ||
<math>~ | <table border="0" cellpadding="5" align="center"> | ||
<tr> | |||
<td align="right"> | |||
<math>~\frac{x_+ - 2x_a + x_-}{\Delta^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x_a'' \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
===Integrating Outward Through the Core=== | |||
From the LAWE for the core, we have, | |||
<div align="center"> | <div align="center"> | ||
<math>~\ | <table border="0" cellpadding="5" align="center"> | ||
| |||
<math>~\ | <tr> | ||
<td align="right"> | |||
<math>~a (g^2 - a^2) x_a''</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- ( 4g^2 - 6a^2 ) x_a' - a \mathfrak{F}_\mathrm{core} x_a \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So, putting these last three expressions together gives an approximate relation between <math>~x_+</math> and the previous two values of the function, <math>~x_-</math> and <math>~x_a</math>, namely, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a (g^2 - a^2) \biggl[ \frac{x_+ - 2x_a + x_-}{\Delta^2} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- ( 4g^2 - 6a^2 ) \biggl[\frac{x_+ - x_-}{2 \Delta} \biggr] - a \mathfrak{F}_\mathrm{core} x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
a (g^2 - a^2) \biggl[ \frac{x_+ }{\Delta^2} \biggr] + ( 4g^2 - 6a^2 ) \biggl[\frac{x_+ }{2 \Delta} \biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a (g^2 - a^2) \biggl[ \frac{2x_a - x_-}{\Delta^2} \biggr] | |||
+ ( 4g^2 - 6a^2 ) \biggl[\frac{x_-}{2 \Delta} \biggr] - a \mathfrak{F}_\mathrm{core} x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\Rightarrow~~~x_+[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) ] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2a (g^2 - a^2) [ 2x_a - x_- ] | |||
+ ( 4g^2 - 6a^2 ) [\Delta x_- ] - 2\Delta^2 a \mathfrak{F}_\mathrm{core} x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a | |||
+ [ \Delta( 4g^2 - 6a^2 ) - 2a (g^2 - a^2)] x_- \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Now, at the very center of the configuration, <math>~(a = 0)</math>, we expect the function, <math>~x(\xi)</math>, to be symmetric; that is, we expect <math>~x_- = x_+</math>. So for this case alone, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
x_+[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) - \Delta( 4g^2 - 6a^2 ) + 2a (g^2 - a^2)] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
x_+[2(g^2 - \cancelto{0}{a^2}) + 2(g^2 - \cancelto{0}{a^2})] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[4 (g^2 - \cancelto{0}{a^2}) - 2\Delta^2 \mathfrak{F}_\mathrm{core} ]x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
x_+ | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ 1 - \frac{\Delta^2 \mathfrak{F}_\mathrm{core}}{2g^2} \biggr]x_a \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
For all other coordinate locations, <math>~a = \xi</math>, in the range, <math>~0 < \xi < 1</math>, we will use the general expression, namely, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\Rightarrow~~~x_+ | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a | |||
+ [ \Delta( 4g^2 - 6a^2 ) - 2a (g^2 - a^2)] x_- }{[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) ] } \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
= | Keep in mind that, when we move across the interface at <math>~a = 1</math>, we want both the value of the function, <math>~x_q</math>, and its first derivative, <math>~x_q'</math>, to be the same as viewed from ''both'' the envelope and the core. In a numerical integration algorithm, it will be very straightforward to set the ''value'' of the eigenfunction at the interface. In order to properly handle the first derivative, I propose that we extend the core solution and evaluate the eigenfunction at one zone beyond the interface, and identify the values of the eigenfunction that straddles the interface as, | ||
<div align="center"> | <div align="center"> | ||
<math>~(x_-)_q</math> and <math>~(x_+)_q</math>. | |||
</div> | |||
Then define the slope of the eigenfunction at the interface by the expression, | |||
<div align="center" id="InterfaceSlope"> | |||
<table border="1" cellpadding="8"> | |||
<tr><td align="center">Slope at the Interface</td></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x_q'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 229: | Line 1,493: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\frac{(x_+)_q - (x_-)_q}{2\Delta} \, .</math> | ||
1 + \biggl(\frac{\ | </td> | ||
\frac{\rho_e}{\rho_c} \biggl(\frac{1}{q^ | </tr> | ||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
===Integrating Outward Through the Envelope=== | |||
From the LAWE for the envelope, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a^2( 1 - q^3 a^3 ) x_a'' </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- ( 3 - 6q^3 a^3 ) a x_a' | |||
- | |||
[ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Inserting the same finite-difference expressions for the first and second derivatives, we therefore have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_+ - 2x_a + x_-}{\Delta^2} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- ( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_+ - x_-}{2 \Delta} \biggr] | |||
- | |||
[ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_+ }{\Delta^2} \biggr] + ( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_+ }{2 \Delta} \biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_-}{2 \Delta} \biggr] | |||
- a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_- - 2x_a }{\Delta^2} \biggr] | |||
- [ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
x_+ [2a^2( 1 - q^3 a^3 ) + \Delta ( 3 - 6q^3 a^3 ) a ] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[ \Delta ( 3 - 6q^3 a^3 ) a | |||
- 2a^2( 1 - q^3 a^3 ) ] x_- + [4a^2( 1 - q^3 a^3 ) | |||
- 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Now, at the interface (only), we need to relate <math>~x_-</math> to <math>~x_+</math> in such a way that the slope gives the proper value at the interface. Specifically, we need to set, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_-</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x_+ - 2\Delta (x_q') \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, <math>~x_q'</math> takes the [[#InterfaceSlope|value that was determined for the core]]. Hence, ''at'' the interface <math>~(a = 1)</math>, the first step into the envelope is special and demands that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
x_+ [2a^2( 1 - q^3 a^3 ) + \Delta ( 3 - 6q^3 a^3 ) a ] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[ \Delta ( 3 - 6q^3 a^3 ) a | |||
- 2a^2( 1 - q^3 a^3 ) ] [x_+ - 2\Delta (x_q')] + [4a^2( 1 - q^3 a^3 ) | |||
- 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
x_+ [4a^2( 1 - q^3 a^3 ) ] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] [- 2\Delta (x_q')] | |||
+ [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-2\Delta [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] x_q' | |||
+ [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
and, setting, <math>~a = 1 ~~~~\Rightarrow ~~~ | |||
x_+ | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ 2\Delta [2( 1 - q^3 ) - \Delta ( 3 - 6q^3 ) ] x_q' | |||
+ [4( 1 - q^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} -\alpha_e ) ] x_a }{ 4( 1 - q^3 ) } \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Varying the Oscillation Frequency== | |||
===Approach=== | |||
First, we fix <math>~q</math>, <math>~\gamma_e</math>, and <math>~\gamma_c</math>; in the example, here ([[#Properties_of_21Analytic_Solution|as above]]) we choose: <math>~(q,\gamma_e,\gamma_c) = ( 0.6840119, 1.1940299, 1.845579)</math>. For this example, we will also retain the constraint, <math>~g^2 = \mathcal{B}</math>, in which case, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\rho_e}{\rho_c} = \frac{2q^3}{1+2q^3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0.3902664 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Next, we pick various values of the (square of the) dimensionless oscillation frequency, <math>~\sigma_c^2</math>, and, in order to ensure that the dimensional frequency in the envelope matches the dimensional frequency of the core, from each value we set, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F}_\mathrm{core} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\sigma_c^2 + 8}{\gamma_c} - 6 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F}_\mathrm{env} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{\gamma_e} \biggl[ \sigma_c^2 \biggl(\frac{\rho_e}{\rho_c} \biggr)^{-1} + 8\biggr]- 6 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
For the finite-difference algorithm, we divide the core — radial coordinate range, <math>~0 \le \xi \le 1</math> — into N<sub>core</sub> zones, and the envelope — radial coordinate range, <math>~1\le \xi \le 1/q</math> — into N<sub>env</sub> zones. This means that the spacing between successive radial zones in the core and envelope is, respectively, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta_c \equiv \frac{1}{\mathrm{N}_\mathrm{core}}</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~\Delta_e \equiv \frac{q^{-1} - 1}{\mathrm{N}_\mathrm{env}} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Starting at the center of the configuration <math>~(\xi = 0)</math>, where we arbitrarily set the value of the eigenfunction to <math>~x_0 = 1</math>, the value of the eigenfunction at the first grid point away from the center <math>~(\xi = \Delta_c)</math> is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
x_{k=1} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ 1 - \frac{\Delta_c^2 \mathfrak{F}_\mathrm{core}}{2g^2} \biggr]x_0 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Thereafter — moving out toward and just beyond the interface location <math>~(\xi = 1)</math>, the radial coordinate of each successive grid point is <math>~\xi_k = k\Delta_c</math>, and the numerically determined value of the eigenfunction at each successive grid point <math>~(k = 1 \rightarrow \mathrm{N}_\mathrm{core})</math> is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
x_{k+1} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{[4\xi_k (g^2 - \xi_k^2) - 2\Delta_c^2 \xi_k \mathfrak{F}_\mathrm{core} ]x_k | |||
+ [ \Delta_c( 4g^2 - 6\xi_k^2 ) - 2\xi_k (g^2 - \xi_k^2)] x_{k-1} }{[2\xi_k (g^2 - \xi_k^2) + \Delta_c( 4g^2 - 6\xi_k^2 ) ] } \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Then, at the interface, which is associated with <math>~k = \mathrm{N}_\mathrm{core}</math>, we define the reference slope as, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_q'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{x_{k+1} - x_{k-1}}{2\Delta_c} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Next, we move outward into the envelope, using the integer index, <math>~n = 1 \rightarrow \mathrm{N}_\mathrm{env}</math>, to label successive radial grid locations <math>~(\xi_n = 1 + n\Delta_e)</math>. Letting the value of the eigenfunction at the interface be represented by <math>~x_q</math>, at the first grid location outside the interface <math>~(\xi = 1 + \Delta_e)</math>, the value of the eigenfunction is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math align="right"> | |||
~x_{n=1} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{ 2\Delta_e [2( 1 - q^3 ) - \Delta_e ( 3 - 6q^3 ) ] x_q' | |||
+ [4( 1 - q^3 ) - 2\Delta_e^2 ( q^3 \mathfrak{F}_\mathrm{env} -\alpha_e ) ] x_q }{ 4( 1 - q^3 ) } \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 237: | Line 1,825: | ||
</table> | </table> | ||
</div> | </div> | ||
we [[User:Tohline/ | |||
Thereafter, moving outward through the envelope to the surface, the value of the eigenfunction at each successive grid location is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
x_{n+1} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{[ \Delta_e ( 3 - 6q^3 \xi_n^3 ) \xi_n - 2\xi_n^2( 1 - q^3 \xi_n^3 ) ] x_{n-1} + [4\xi_n^2( 1 - q^3 \xi_n^3 ) | |||
- 2\Delta_e^2 ( q^3 \mathfrak{F}_\mathrm{env} \xi_n^3 -\alpha_e ) ] x_{n} }{ [2\xi_n^2( 1 - q^3 \xi_n^3 ) + \Delta_e ( 3 - 6q^3 \xi_n^3 ) \xi_n ] } \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<font color="red"><b>TEST:</b></font> We tested this finite-difference algorithm on a grid of resolution, <math>~\mathrm{N}_\mathrm{core} = \mathrm{N}_\mathrm{core} = 50</math>, by first setting <math>~\sigma_c^2 = 28.91158</math>. The resulting, numerically constructed eigenfunction matched to high accuracy the analytically generated eigenfunction shown, above, as [[#Figure1|Figure 1]]; see also, the middle image in the top panel of [[#Figure2|Figure 2]]. Representative values of the numerically determined eigenfunction, <math>~x(\xi)</math> at various discrete grid locations are provided in Table 1, along with the numerically determined value of the slope at the interface, <math>~x_q'</math>. At each grid location, the associated value of the dimensionless radius, <math>~r/R</math>, may be obtained by simply multiplying each tabulated value of <math>~\xi</math> by the parameter, <math>~q</math>. | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr> | |||
<th align="center" colspan="7"> | |||
<font size="+1">Table 1:</font><br /> | |||
Example Numerical Determination of Eigenfunction | |||
</th> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="7"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(q,\gamma_e,\gamma_c)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(0.684012, 1.194030, 1.845579)</math> | |||
</td> | |||
</tr> | |||
<tr><td align="center" colspan="3">and</td></tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
<math>~\sigma_c^2 = 28.91158</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<th align="center" colspan="3">Core</th> | |||
<td align="center" rowspan="10"> </td> | |||
<th align="center" colspan="3">Envelope</th> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~g^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1.323609</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F}_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~14</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta_c</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0.02</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
<td align="center" colspan="3"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\alpha_e </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-0.35</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F}_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~62.74338</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta_e</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~0.00923926</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~k</math></td> | |||
<td align="center"><math>~\xi</math></td> | |||
<td align="center"><math>~x</math></td> | |||
<td align="center"><math>~n</math></td> | |||
<td align="center"><math>~\xi</math></td> | |||
<td align="center"><math>~x</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">0</td> | |||
<td align="center">0.00</td> | |||
<td align="center">1.000000</td> | |||
<td align="center">0</td> | |||
<td align="center">1.00</td> | |||
<td align="center">-0.057649</td> | |||
</tr> | |||
<tr> | |||
<td align="center">1</td> | |||
<td align="center">0.02</td> | |||
<td align="center">0.997885</td> | |||
<td align="center">1</td> | |||
<td align="center">1.0092393</td> | |||
<td align="center">-0.076955</td> | |||
</tr> | |||
<tr> | |||
<td align="center">2</td> | |||
<td align="center">0.04</td> | |||
<td align="center">0.997182</td> | |||
<td align="center">2</td> | |||
<td align="center">1.0184785</td> | |||
<td align="center">-0.095792</td> | |||
</tr> | |||
<tr> | |||
<td align="center"><math>~\vdots</math></td> | |||
<td align="center"><math>~\vdots</math></td> | |||
<td align="center"><math>~\vdots</math></td> | |||
<td align="center"><math>~\vdots</math></td> | |||
<td align="center"><math>~\vdots</math></td> | |||
<td align="center"><math>~\vdots</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">49</td> | |||
<td align="center">0.98</td> | |||
<td align="center">-0.015811</td> | |||
<td align="center">49</td> | |||
<td align="center">1.452724</td> | |||
<td align="center">0.466484</td> | |||
</tr> | |||
<tr> | |||
<td align="center">50</td> | |||
<td align="center">1.00</td> | |||
<td align="center">-0.057649</td> | |||
<td align="center">50</td> | |||
<td align="center">1.461963</td> | |||
<td align="center">0.535957</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"><math>~x_q' = -2.113043</math></td> | |||
<td align="center" colspan="3"> </td> | |||
</tr> | |||
</table> | |||
===Results=== | |||
====Motivated by Analytic21==== | |||
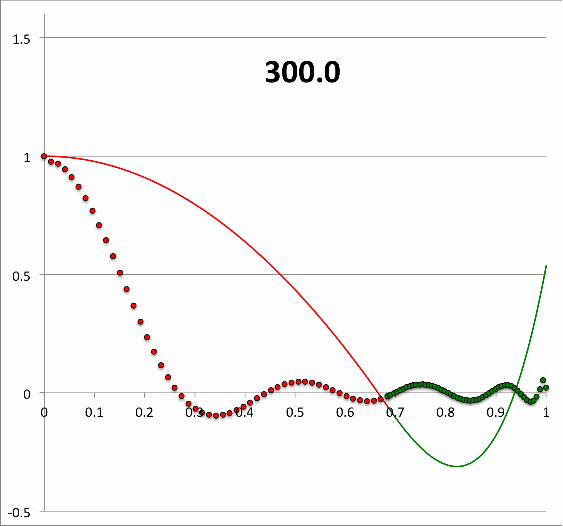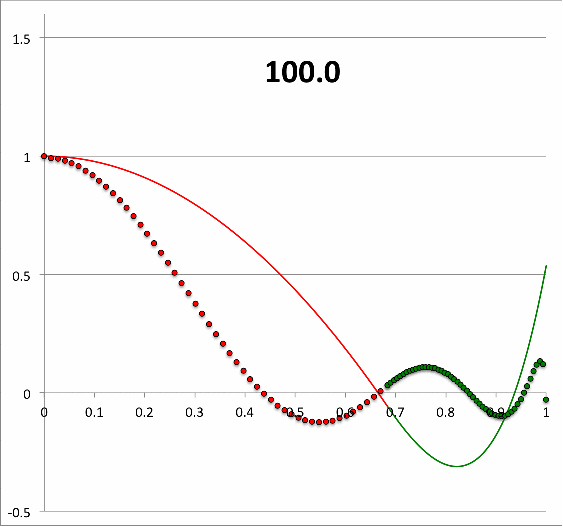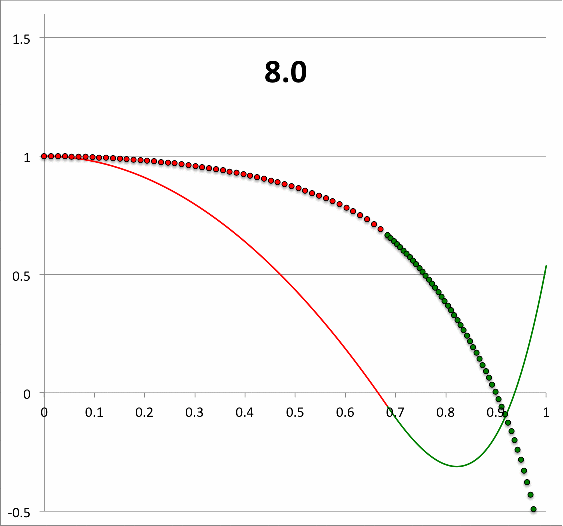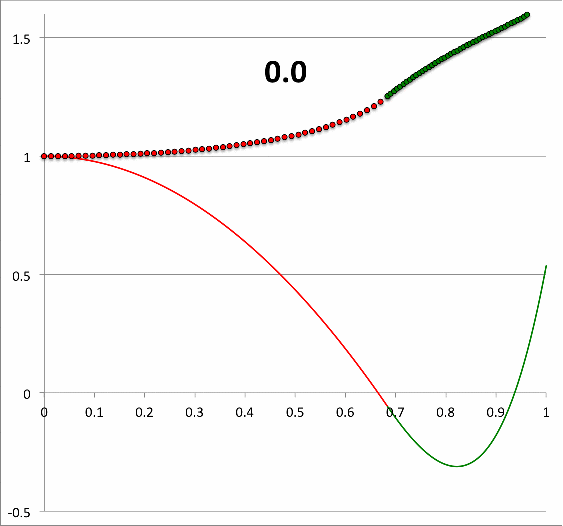
Continuing with our analysis of the equilibrium model that is defined by the parameters, <math>~(q,\gamma_e,\gamma_c) = ( 0.6840119, 1.1940299, 1.845579)</math>, we have used the above-described numerical algorithm, to construct 26 different eigenfunctions that simultaneously satisfy the LAWE of the core and the LAWE of the envelope for 26 different values of <math>~\sigma_c^2</math> in the range, <math>~300 \ge \sigma_c^2 \ge 0</math>. The curve traced by a sequence of small circular markers (red = core; green = envelope) in the bottom panel of Figure 2 displays each of these numerically constructed eigenfunctions in succession — in order of ''decreasing'' values of <math>~\sigma_c^2</math> — in the form of a looped animation sequence. Also displayed in each frame of the animation, for reference, is the relevant value of <math>~\sigma_c^2</math>, as well as an unchanging, smooth, thin red/green curve that traces the ''analytically'' derived eigenfunction shown in Figure 1, for which <math>~\sigma_c^2 = 28.91158</math>. | |||
<div align="center" id="Figure2"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr><th align="center"> | |||
<font size="+1">Figure 2:</font><br /> | |||
<br /> | |||
<math>~(q,\gamma_e,\gamma_c) = ( 0.6840119, 1.1940299, 1.845579)</math> | |||
</th></tr> | |||
<tr><td align="center"> | |||
[[File:ImageTrio.png|500px|center|Three movie frames]] | |||
</td></tr> | |||
<tr><td align="center"> | |||
[[File:EigenfunctionMovie1.gif|500px|center|Eigenfunction movie]] | |||
</td></tr> | |||
</table> | |||
</div> | |||
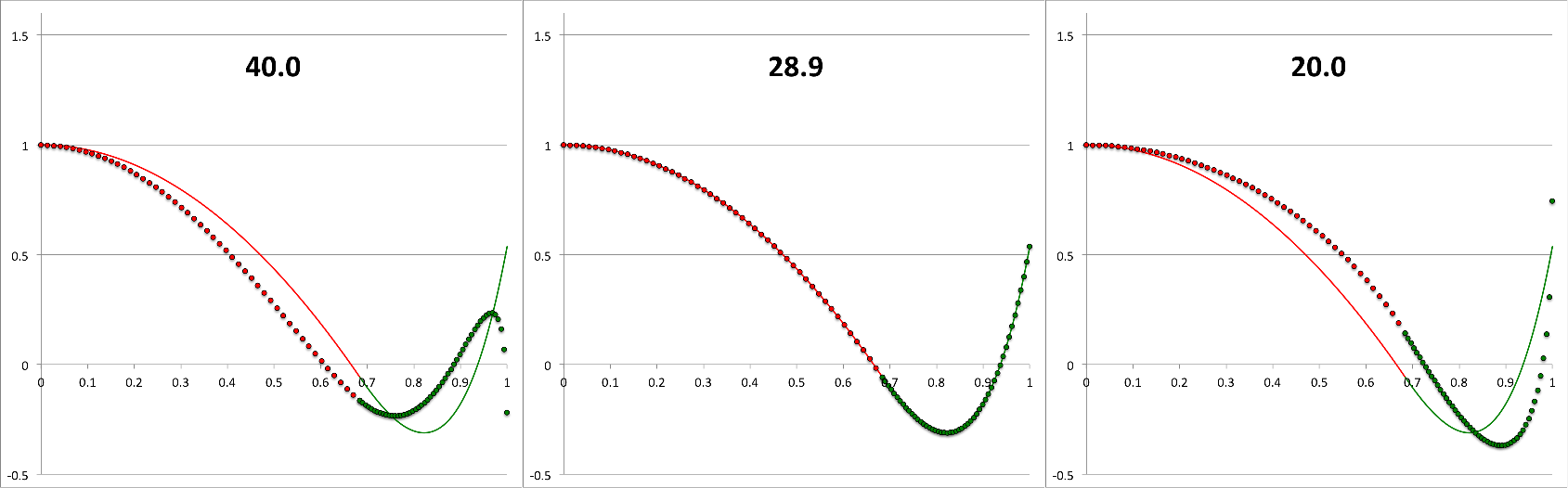
Three frames from the animation sequence have been displayed side-by-side in the top panel of Figure 2. This image montage is presented, in part, to illustrate the degree to which our numerically generated eigenfunction matches the analytically generated eigenfunction in the ''specific'' case <math>~(\sigma_c^2 = 28.9)</math> for which we have been able to obtain an analytic solution to the combined/matched, core/envelope LAWEs. | |||
====Motivated by Analytic22==== | |||
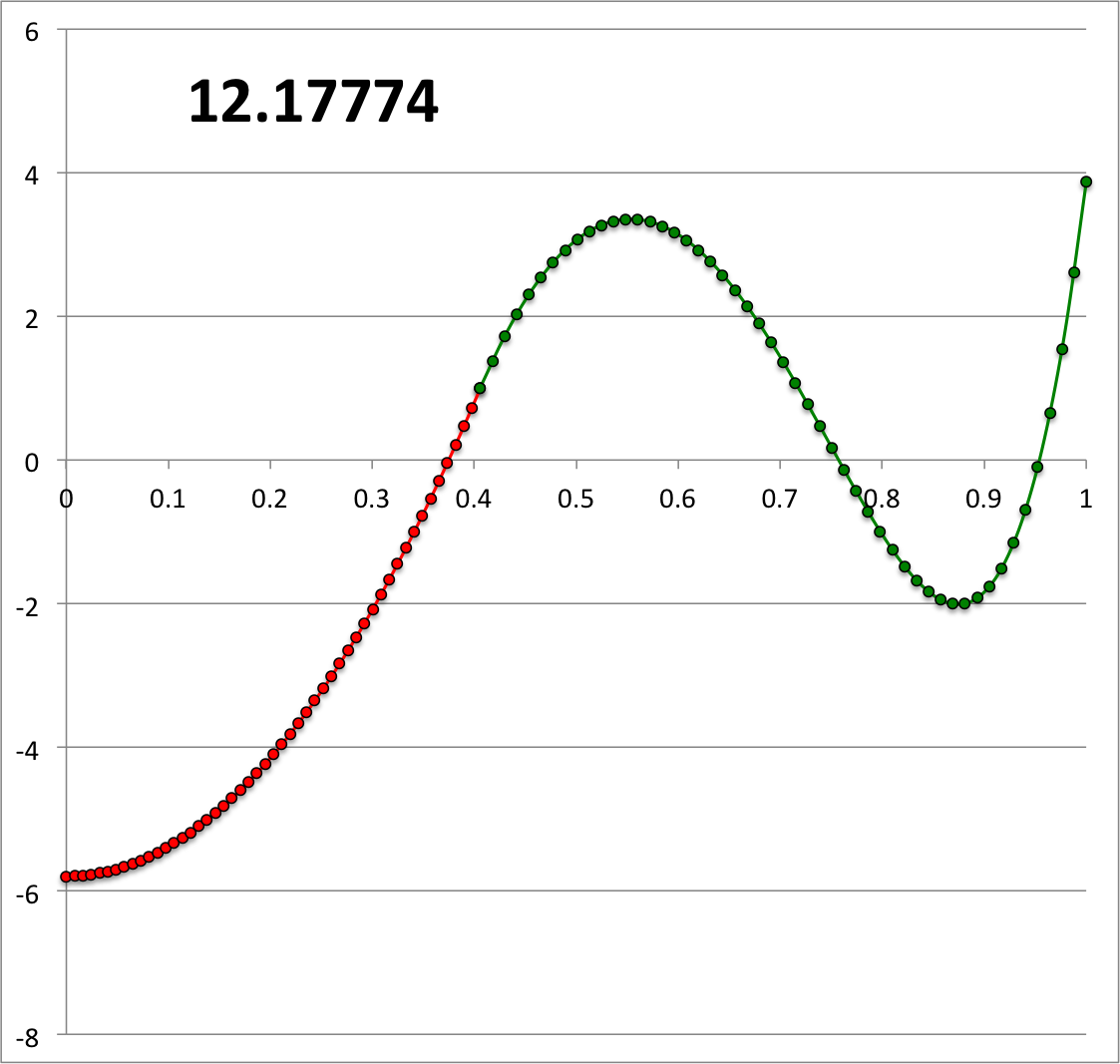
We have also numerically constructed an eigenfunction that matches our [[User:Tohline/Appendix/Ramblings/Additional_Analytically_Specified_Eigenvectors_for_Zero-Zero_Bipolytropes#Illustration22|accompanying analytic Illustration22]]. In Figure 3, the numerically derived solution has been plotted on top of the analytically derived solution. | |||
<div align="center" id="Figure3"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr><th align="center"> | |||
<font size="+1">Figure 3:</font><br /> | |||
<br /> | |||
<math>~(q,\gamma_e,\gamma_c) = ( 0.886575, 1.798817, 1.021798)</math> | |||
</th></tr> | |||
<tr><td align="center"> | |||
[[File:NumericalModel22.png|350px|center|Numerically generated eigenfunction plotted on top of the analytically derived, Illustration22]] | |||
</td></tr> | |||
</table> | |||
</div> | |||
====Motivated by Analytic31==== | |||
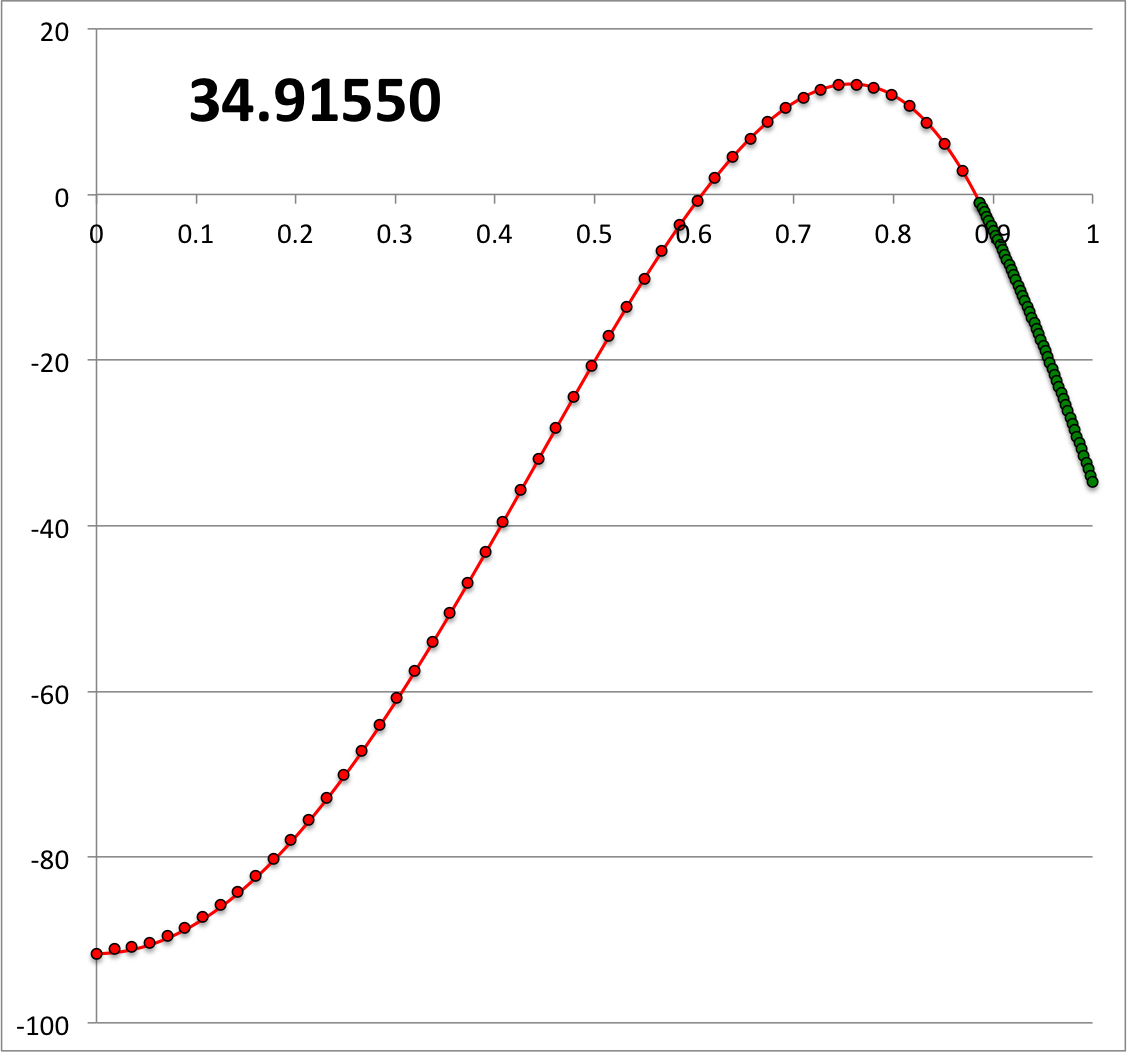
We have also numerically constructed an eigenfunction that matches our [[User:Tohline/Appendix/Ramblings/Additional_Analytically_Specified_Eigenvectors_for_Zero-Zero_Bipolytropes#Illustration31|accompanying analytic Illustration31]]. In Figure 4, the numerically derived solution has been plotted on top of the analytically derived solution. | |||
<div align="center" id="Figure4"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr><th align="center"> | |||
<font size="+1">Figure 4:</font><br /> | |||
<br /> | |||
<math>~(q,\gamma_e,\gamma_c) = ( 0.4059596, 1.180462, 1.008887)</math> | |||
</th></tr> | |||
<tr><td align="center"> | |||
[[File:NumericanModel31.png|350px|center|Numerically generated eigenfunction plotted on top of the analytically derived, Illustration31]] | |||
</td></tr> | |||
</table> | |||
</div> | |||
==Unconstrained LAWEs== | |||
Here we use the most general expressions for the pair of governing LAWEs; that is, we will ''not'' force <math>~g^2 = \mathcal{B}</math>. Drawing from our most general summary discussion, the [[User:Tohline/SSC/Stability/BiPolytrope0_0#The_Core.27s_LAWE|LAWE for the core]] is, | |||
<div align="center"> | <div align="center"> | ||
| Line 259: | Line 2,111: | ||
</table> | </table> | ||
</div> | </div> | ||
where, | where, | ||
<div align="center"> | <div align="center"> | ||
<math>~\eta \equiv \frac{\xi}{g} \, ,</math> | <math>~\eta \equiv \frac{\xi}{g} \, ,</math> | ||
and | and | ||
<math>~\mathfrak{F}_\mathrm{core} \equiv \frac{3\omega_\mathrm{core}^2}{2\pi G\gamma_c \rho_c} - 2\alpha_c\, .</math> | <math>~\mathfrak{F}_\mathrm{core} \equiv \frac{3\omega_\mathrm{core}^2}{2\pi G\gamma_c \rho_c} - 2\alpha_c = \frac{(\sigma_c^2 +8)}{\gamma_c} -6 \, ,</math> | ||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~g^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
1 + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( 1-q \biggr) + | |||
\frac{\rho_e}{\rho_c} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
Hence, we may also write the core's LAWE as, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
=== | <tr> | ||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(g^2 - \xi^2)\frac{d^2x}{d\xi^2} + | |||
( 4g^2 - 6\xi^2 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} | |||
+ \mathfrak{F}_\mathrm{core} x \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and we should be able to numerically integrate from the center, outward through the core, exactly as [[#Integrating_Outward_Through_the_Core|described above]]. | |||
Separately, the [[User:Tohline/SSC/Stability/BiPolytrope0_0#The_Envelope.27s_LAWE|LAWE for the envelope]] is, | |||
<div align="center"> | <div align="center"> | ||
| Line 288: | Line 2,180: | ||
\frac{1}{\xi} \cdot \frac{dx}{d\xi} | \frac{1}{\xi} \cdot \frac{dx}{d\xi} | ||
+ \biggl[ | + \biggl[ | ||
\mathcal{D} | \mathcal{D} \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e | ||
\biggr]\frac{x}{\xi^2} \, , | \biggr]\frac{x}{\xi^2} \, , | ||
</math> | </math> | ||
| Line 348: | Line 2,240: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{3\omega^2_\mathrm{env}}{2\pi G \gamma_e \rho_e} - 2\alpha_e | <math>~\frac{3\omega^2_\mathrm{env}}{2\pi G \gamma_e \rho_e} - 2\alpha_e = \frac{1}{\gamma_e}\biggl[\frac{\sigma_c^2}{(\rho_e/\rho_c)} + 8\biggr] - 6 | ||
\, . | \, . | ||
</math> | </math> | ||
| Line 355: | Line 2,247: | ||
</table> | </table> | ||
</div> | </div> | ||
After defining the new parameter, | |||
<div align="center"> | <div align="center"> | ||
<math>~ | <math>~\mathcal{H} \equiv \frac{g^2 - \mathcal{B}}{\mathcal{A}} \, ,</math> | ||
</div> | </div> | ||
this LAWE for the envelope may be written as, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 377: | Line 2,259: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) x_a'' </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 383: | Line 2,265: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
- ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a x_a' | |||
- | |||
[ \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Inserting the same finite-difference expressions for the first and second derivatives, we therefore have, | |||
<div align="center"> | <div align="center"> | ||
| Line 400: | Line 2,281: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )\biggl[ \frac{x_+ - 2x_a + x_-}{\Delta^2} \biggr] </math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a \biggl[ \frac{x_+ - x_-}{2 \Delta} \biggr] | |||
- [ \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )\biggl[ \frac{x_+ }{\Delta^2} \biggr] | |||
+ ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a \biggl[ \frac{x_+ }{2 \Delta} \biggr] | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 407: | Line 2,305: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a \biggl[ \frac{x_-}{2 \Delta} \biggr] | ||
- a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )\biggl[ \frac{x_-}{\Delta^2} \biggr] | |||
- [ \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a + a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )\biggl[ \frac{2x_a }{\Delta^2} \biggr] | |||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 417: | Line 2,314: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~x_+ [2 a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) | |||
+ \Delta ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a ] | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 423: | Line 2,322: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
x_- [ \Delta( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a | |||
- 2a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )] | |||
+ ( | + x_a [ 4a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) | ||
- 2\Delta^2( \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] \, . | |||
\, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 435: | Line 2,332: | ||
</table> | </table> | ||
</div> | </div> | ||
Now, at the interface (only), we need to relate <math>~x_-</math> to <math>~x_+</math> in such a way that the slope gives the proper value at the interface. Specifically, we need to set, | |||
<div align="center"> | <div align="center"> | ||
<math>~ | <table border="0" cellpadding="5" align="center"> | ||
</ | |||
<tr> | |||
< | <td align="right"> | ||
<math>~ | <math>~x_-</math> | ||
</td> | |||
<math>~ | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x_+ - 2\Delta (x_q') \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
where, <math>~x_q'</math> takes the [[#InterfaceSlope|value that was determined for the core]]. Hence, ''at'' the interface <math>~(a = 1)</math>, the first step into the envelope is special and demands that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 451: | Line 2,356: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{F}_\mathrm{env}</math> | <math>~x_+ [2 a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) | ||
+ \Delta ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a ] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[x_+ - 2\Delta (x_q')][ \Delta( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a | |||
- 2a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )] | |||
+ x_a [ 4a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) | |||
- 2\Delta^2( \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ x_+ [4 a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) ] | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 457: | Line 2,382: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- 2\Delta [ \Delta( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a | |||
- 2a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )] x_q' | |||
+ x_a [ 4a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) | |||
- 2\Delta^2( \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 463: | Line 2,393: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ | and, setting, <math>~a = 1 ~~~~\Rightarrow ~~~ | ||
x_+ | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 469: | Line 2,401: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ \Delta [ 2( 1 + \mathcal{H} - \mathcal{D} )- \Delta( 3 +4\mathcal{H} - 6 \mathcal{D} ) ] x_q' | |||
+ x_a [ 2( 1 + \mathcal{H} - \mathcal{D} ) | |||
- \Delta^2( \mathcal{D} \mathfrak{F}_\mathrm{env} -\alpha_e ) ] }{ 2 ( 1 + \mathcal{H} - \mathcal{D} ) } \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 475: | Line 2,411: | ||
</div> | </div> | ||
=Discussion= | |||
==Conclusions== | |||
Initially, I was surprised to find that, by employing our above-described numerical algorithm, we were able to solve the combined/matched LAWEs for a continuum set — rather than a discrete set — of dimensionless oscillation frequencies, <math>~\sigma_c^2</math>. After all, I have been taught to believe that radial oscillation modes are obtained by solving an eigenvalue problem. After a bit of thought, I recognized that the continuum set of solutions has been obtained in the absence of a specified ''surface'' boundary condition. I suspect that the continuum of solutions can only be relevant to a real ''astrophysical'' problem after a physically meaningful surface boundary condition has been imposed; for example, a specification of the ''slope'' of the eigenfunction at the equilibrium configuration's surface. This should naturally reduce the continuum set to a discrete set of eigenvectors. | |||
Watching the animation sequence reveals, for example, that as the value of <math>~\sigma_c^2</math> is reduced, the number of nodes inside the configuration is reduced, in a predictable, quantized fashion. At the same time — between each drop in the integer number of nodes — the slope of the eigenfunction at the surface <math>~(r/R = 1)</math> varies between large positive, and large negative values. Hence, we should be able to find a matched solution whose slope at the surface ''also'' matches any reasonably specified boundary condition. | |||
==Additional Possibilities== | |||
* We should be able to ''numerically'' identify a wide range of quantized radial modes of oscillation by specifying a physically reasonable surface slope then, for each successive quantum node count, tuning the choice of <math>~\sigma_c^2</math> until the desired slope has been encountered. | |||
* It seems unlikely that any of our analytically derived eigenfunctions will happen to satisfy the specified boundary condition. The analytic functions have nevertheless proven to be useful in the sense that they provide a terrific check for the computational algorithm that, then, can be used to identify physically meaningful solutions numerically. | |||
* Tie this new (numerical) technique into the [[User:Tohline/SSC/Stability/BiPolytrope0_0CompareApproaches#Comparing_Stability_Analyses_of_Zero-Zero_Bipolytropes|associated discussion]] of the relationship between stability determinations via LAWEs and global free-energy considerations. | |||
* The Figure 2 animation displays numerically determined solutions, <math>~x(r/R)</math>, to the combined/matching LAWEs only for ''non-negative'' values of <math>~\sigma_c^2</math>; these should be relevant only to ''stable'' radial oscillations. We should also see what can be learned from solutions associated with ''negative'' values of <math>~\sigma_c^2</math>, which may be relevant to unstable radial modes of oscillation. | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Latest revision as of 22:59, 3 February 2017
Numerically Determined Eigenvectors of a Zero-Zero Bipolytrope
Here we build on the analytic foundation summarized in an accompanying chapter and attempt to numerically construct a variety of eigenvectors that describe radial oscillations of bipolytropes for which, <math>~(n_c, n_e) = (0,0)</math>.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Setup
We'll begin with the linear-adiabatic wave equations that describe oscillations of the core and envelope, separately. We also will immediately restrict our investigation to configurations for which,
<math>~g^2 = \mathcal{B} </math> <math>~\Rightarrow</math> <math>~g^2 = \frac{1+8q^3}{ (1+2q^3)^2 } \, ,</math> and, <math>~q^3 = \mathcal{D} = \biggl[ \frac{\rho_e/\rho_c}{2(1-\rho_e/\rho_c)} \biggr] </math> <math>~\Rightarrow</math> <math>~\frac{\rho_e}{\rho_c} = \frac{2q^3}{1+2q^3} \, .</math>
For the core we have,
|
<math>~0</math> |
<math>~=</math> |
<math>~ (1 - \eta^2)\frac{d^2x}{d\eta^2} + ( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx}{d\eta} + \mathfrak{F}_\mathrm{core} x \, , </math> |
where,
<math>~\eta \equiv \frac{\xi}{g} \, ,</math> and <math>~\mathfrak{F}_\mathrm{core} \equiv \frac{3\omega_\mathrm{core}^2}{2\pi G\gamma_c \rho_c} - 2\alpha_c\, .</math>
And, for the envelope we have,
|
<math>~0</math> |
<math>~=</math> |
<math>~ ( 1 - q^3 \xi^3 ) \frac{d^2x}{d\xi^2} + ( 3 - 6q^3 \xi^3 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ q^3 \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e \biggr]\frac{x}{\xi^2} \, , </math> |
where,
|
<math>~\mathfrak{F}_\mathrm{env}</math> |
<math>~\equiv</math> |
<math>~\frac{3\omega^2_\mathrm{env}}{2\pi G \gamma_e \rho_e} - 2\alpha_e \, . </math> |
Initial Focus
Properties of 21Analytic Solution
| Figure 1 |
|---|
|
Same analytic, <math>~(\ell,j) = (2,1)</math> eigenfunction as here, but renormalized to unity at the center; numerical label provides value of <math>~\sigma_c^2</math>. |
Evidently, one analytic solution with quantum numbers, <math>~(\ell,j) = (2,1)</math>, shown again here on the right, is available for a zero-zero bipolytrope that has the following properties:
|
<math>~q</math> |
<math>~\approx</math> |
<math>~0.6840119</math> |
|
<math>~\frac{\rho_e}{\rho_c} = \frac{2q^3}{1+2q^3}</math> |
<math>~\approx</math> |
<math>~0.3902664</math> |
|
<math>~\gamma_e = \frac{4}{3+0.35}</math> |
<math>~\approx</math> |
<math>~1.1940299</math> |
|
<math>~\gamma_c </math> |
<math>~\approx</math> |
<math>~1.845579</math> |
|
<math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G \rho_c} = 20\gamma_c - 8 </math> |
<math>~\approx</math> |
<math>~28.91158 \, .</math> |
This means, as well, that,
|
<math>~c_0 \equiv \sqrt{1+\alpha_e} - 1</math> |
<math>~=</math> |
<math>~\sqrt{0.65}-1 \approx - 0.1937742</math> |
|
<math>~g^2 \equiv \frac{1+8q^3}{(1+2q^3)^2}</math> |
<math>~\approx</math> |
<math>~1.3236092</math> |
|
<math>~\mathfrak{F}_\mathrm{core} \equiv \frac{\sigma_c^2 + 8}{\gamma_c} - 6</math> |
<math>~=</math> |
<math>~14</math> |
|
<math>~\mathfrak{F}_\mathrm{env} \equiv \frac{1}{\gamma_e} \biggl[ \sigma_c^2 \biggl(\frac{\rho_c}{\rho_e} \biggr) + 8\biggr]- 6</math> |
<math>~=</math> |
<math>~(c_0^2 + 17c_0 +66) = 62.743385</math> |
In the envelope, the analytically defined eigenfunction is given by the expression,
|
<math>~x_{\ell=2} |_\mathrm{env}</math> |
<math>~=</math> |
<math>~ \xi^{c_0}\biggl[ \frac{ 1 + q^3 A_{21} \xi^{3} + q^6 A_{21}B_{21}\xi^{6} }{ 1 + q^3 A_{21} + q^6 A_{21}B_{21}}\biggr] \, , </math> |
where,
|
<math>~A_{21}</math> |
<math>~\equiv</math> |
<math>~-\biggl( \frac{ 4c_0 + 22}{2c_0 + 5}\biggr) \approx -4.6016533 \, ,</math> |
|
<math>~B_{21}</math> |
<math>~\equiv</math> |
<math>~-\biggl( \frac{c_0 + 7 }{2c_0+8}\biggr) \approx -0.8940912 \, ; </math> |
and in the core, it is,
|
<math>~x_{j=1} |_\mathrm{core}</math> |
<math>~=</math> |
<math>~ \frac{5(1+8q^3) - 7 (1+2q^3)^2 \xi^2}{5(1+8q^3)-7(1+2q^3)^2} \, .</math> |
More succinctly we have,
|
<math>~x_\mathrm{core}</math> |
<math>~=</math> |
<math>~-17.326820 + 18.326820~\xi^2 \, ;</math> |
and,
|
<math>~a \cdot x_\mathrm{env}</math> |
<math>~=</math> |
<math>~ \xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \, , </math> |
where,
<math>~a \equiv -[ 1 + q^3 A_{21} + q^6 A_{21}B_{21}] \approx - 0.05128445 \, .</math>
Demonstrate Core Solution
This means that,
|
<math>~\frac{dx_\mathrm{core}}{d\xi}</math> |
<math>~=</math> |
<math>~36.65364~\xi \, ,</math> |
and,
|
<math>~\frac{d^2x_\mathrm{core}}{d\xi^2}</math> |
<math>~=</math> |
<math>~36.65364 \, .</math> |
Therefore, the LAWE for the core becomes,
|
<math>~[\mathrm{LAWE}]_\mathrm{core}</math> |
<math>~=</math> |
<math>~ (1 - \eta^2)\frac{d^2x_\mathrm{core}}{d\eta^2} + ( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx_\mathrm{core}}{d\eta} + \mathfrak{F}_\mathrm{core} x_\mathrm{core} </math> |
|
|
<math>~=</math> |
<math>~ (g^2 - \xi^2)\frac{d^2x_\mathrm{core}}{d\xi^2} + ( 4g^2 - 6\xi^2 ) \frac{1}{\xi} \cdot \frac{dx_\mathrm{core}}{d\xi} + \mathfrak{F}_\mathrm{core} x_\mathrm{core} </math> |
|
|
<math>~=</math> |
<math>~ 36.65364(1.3236092 - \xi^2) + 36.65364( 5.2944368 - 6\xi^2 ) + 14( -17.326820 + 18.326820~\xi^2) </math> |
|
|
<math>~=</math> |
<math>~ 36.65364(1.3236092 ) + 36.65364( 5.2944368 ) + 14( -17.326820 ) + [36.65364(-1) + 36.65364( - 6 ) + 14( 18.326820)]\xi^2 </math> |
|
|
<math>~=</math> |
<math>~ 36.65364(6.618046 ) - 14( 17.326820 ) + 36.65364 [-1 - 6 + 7]\xi^2 </math> |
|
|
<math>~=</math> |
<math>~ 0 \, . </math> |
Q.E.D.
Demonstrate Envelope Solution
Given that,
|
<math>~a\cdot x_\mathrm{env}</math> |
<math>~=</math> |
<math>~ \xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \, , </math> |
we deduce that,
|
<math>~a\cdot \frac{dx_\mathrm{env}}{d\xi}</math> |
<math>~=</math> |
<math>~ -0.1937742~ \xi^{- 1.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] + \xi^{- 0.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] \, , </math> |
and,
|
<math>~a \cdot \frac{d^2x_\mathrm{env}}{d\xi^2}</math> |
<math>~=</math> |
<math>~ 0.2313226~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] - 2 \times 0.1937742~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math> |
|
|
|
<math>~ + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] \, . </math> |
Therefore, the LAWE for the envelope becomes,
|
<math>~a\cdot [\mathrm{LAWE}]_\mathrm{env}</math> |
<math>~=</math> |
<math>~ a( 1 - q^3 \xi^3 ) \frac{d^2x}{d\xi^2} + a( 3 - 6q^3 \xi^3 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + a\biggl[ q^3 \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e \biggr]\frac{x}{\xi^2} \, , </math> |
|
|
<math>~=</math> |
<math>~ a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{3}{\xi} \cdot \frac{dx}{d\xi} -\alpha_e \biggl(\frac{x}{\xi^2} \biggr) \biggr\} - a q^3 \xi^3 \biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} - \mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr)\biggr\} \, . </math> |
Now, the first of these sub-expressions gives,
|
<math>~ a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{3}{\xi} \cdot \frac{dx}{d\xi} -\alpha_e \biggl(\frac{x}{\xi^2} \biggr) \biggr\} </math> |
<math>~=</math> |
<math>~ 0.2313226~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] - 2 \times 0.1937742~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math> |
|
|
|
<math>~ + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] </math> |
|
|
|
<math>~ -0.5813226~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] + 3\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math> |
|
|
|
<math>~+0.35 \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ (0.2313226 -0.5813226 + 0.35) ~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math> |
|
|
|
<math>~ + (3 - 2 \times 0.1937742)~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ (3 - 2 \times 0.1937742)~ \xi^{- 2.1937742}\biggl[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} \biggr] + \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \xi^{- 2.1937742}\biggl[ -20.37783~ \xi^3 + 19.24657~\xi^{6} \biggr]
</math> |
And the sub-expression inside the second set of curly braces gives,
|
<math>~ a\biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} -\mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr) \biggr\} </math> |
<math>~=</math> |
<math>~ 0.2313226~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] - 2 \times 0.1937742~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math> |
|
|
|
<math>~ + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] </math> |
|
|
|
<math>~ -1.1626452~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] + 6\xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] </math> |
|
|
|
<math>~- 62.74339 \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ (0.2313226 -1.1626452 - 62.74339)~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math> |
|
|
|
<math>~ + (6- 2 \times 0.1937742)~ \xi^{- 1.1937742}\biggl[ - 4.4180043~ \xi^{2} + 2.5283016~\xi^{5} \biggr] + \xi^{- 0.1937742}\biggl[ -8.8360086~ \xi + 12.641508~\xi^{4} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -63.67471~ \xi^{- 2.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] </math> |
|
|
|
<math>~ + 5.612452~ \xi^{- 2.1937742}\biggl[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} \biggr] + \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \xi^{- 2.1937742}\biggl[ -63.67471 + 93.77171~ \xi^{3} -26.83148~\xi^{6} \biggr] </math> |
|
|
|
<math>~ + ~ \xi^{- 2.1937742}\biggl[ - 24.79584~ \xi^{3} + 14.18997~\xi^{6} \biggr] + \xi^{- 2.1937742}\biggl[ -8.8360086~ \xi^3 + 12.641508~\xi^{6} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \xi^{- 2.1937742}\biggl[ -63.67471 + (93.77171-24.79584- 8.8360086) ~ \xi^{3} + (-26.83148+14.18997 + 12.641508)~\xi^{6} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \xi^{- 2.1937742}\biggl[ -63.67471 + 60.13986 ~ \xi^{3} \biggr] </math> |
|
<math>~\Rightarrow~~~ a(q^3\xi^3) \biggl\{ \frac{d^2x}{d\xi^2} + \frac{6}{\xi} \cdot \frac{dx}{d\xi} -\mathfrak{F}_\mathrm{env} \biggl(\frac{x}{\xi^2} \biggr) \biggr\} </math> |
<math>~=</math> |
<math>~ \xi^{- 2.1937742}\biggl[ -20.37783 +19.24657 ~ \xi^{6} \biggr] \, . </math> |
But these two sub-expressions cancel precisely, which means that our eigenfunction satisfies the LAWE! Q.E.D.
Boundary Conditions
Notice that for this particular eigenfunction solution, the value and first radial derivative at the center <math>~(\xi=0)</math> of the configuration is,
|
<math>~x_\mathrm{core}</math> |
<math>~=</math> |
<math>~-17.326820 + 18.326820~\cancelto{0}{\xi^2} = -17.326820 \, ;</math> |
and,
|
<math>~\frac{dx_\mathrm{core}}{d\xi}</math> |
<math>~=</math> |
<math>~36.65364~\cancelto{0}{\xi} = 0 \, .</math> |
And, at the surface <math>~(\xi = q^{-1}) </math> the value and first radial derivative are,
|
<math>~a \cdot x_\mathrm{env}</math> |
<math>~=</math> |
<math>~ \biggl\{\xi^{- 0.1937742}\biggl[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} \biggr] \biggr\}_{\xi=1/q} </math> |
|
|
<math>~\approx</math> |
<math>~ 0.47627246\, , </math> |
where,
<math>~a \approx - 0.05128445 \, ;</math>
and,
|
<math>~\frac{d\ln x_\mathrm{env}}{d\ln \xi} </math> |
<math>~=</math> |
<math>~ \frac{\xi}{a\cdot x_\mathrm{env}} \biggl[ a\cdot \frac{dx_\mathrm{env}}{d\xi} \biggr]</math> |
|
|
<math>~=</math> |
<math>~ \frac{ -0.1937742~\xi^{- 0.1937742}[ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] + \xi^{- 0.1937742}[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{\xi^{- 0.1937742} [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } </math> |
|
|
<math>~=</math> |
<math>~ -0.1937742 + \frac{~ [ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{ [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } </math> |
|
<math>~\Rightarrow ~~~ \biggl\{ \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr\}_{\xi=1/q} </math> |
<math>~=</math> |
<math>~ -0.1937742 + \biggl\{ \frac{[ - 4.4180043~ \xi^{3} + 2.5283016~\xi^{6} ] }{ [ 1 - 1.4726681~ \xi^{3} + 0.4213836~\xi^{6} ] } \biggr\}_{\xi=1/q} </math> |
|
|
<math>~=</math> |
<math>~ -0.1937742 + 21.22492 = 21.03115 \, . </math> |
Finite-Difference Representation
General Approach
Working with the Taylor series expansion, we can write,
|
<math>~x(\xi)</math> |
<math>~\approx</math> |
<math>~ x(a) + (\xi - a) x_a' + \tfrac{1}{2} (\xi-a)^2 x_a \, , </math> |
and letting <math>~\xi_\pm = a \pm \Delta </math>, we have,
|
<math>~x_+</math> |
<math>~\approx</math> |
<math>~ x(a) + \Delta \cdot x_a' + \tfrac{1}{2} \Delta^2 x_a \, , </math> |
and,
|
<math>~x_-</math> |
<math>~\approx</math> |
<math>~ x(a) - \Delta \cdot x_a' + \tfrac{1}{2} \Delta^2 x_a \, . </math> |
Subtracting the second of these two expressions from the first gives,
|
<math>~x_+ - x_-</math> |
<math>~\approx</math> |
<math>~ 2 \Delta \cdot x_a' </math> |
|
<math>~\Rightarrow ~~~ x_a'</math> |
<math>~\approx</math> |
<math>~ \frac{x_+ - x_-}{2 \Delta} \, ; </math> |
while, adding the two expressions together gives,
|
<math>~\frac{x_+ - 2x_a + x_-}{\Delta^2}</math> |
<math>~\approx</math> |
<math>~ x_a \, . </math> |
Integrating Outward Through the Core
From the LAWE for the core, we have,
|
<math>~a (g^2 - a^2) x_a</math> |
<math>~=</math> |
<math>~ - ( 4g^2 - 6a^2 ) x_a' - a \mathfrak{F}_\mathrm{core} x_a \, . </math> |
So, putting these last three expressions together gives an approximate relation between <math>~x_+</math> and the previous two values of the function, <math>~x_-</math> and <math>~x_a</math>, namely,
|
<math>~a (g^2 - a^2) \biggl[ \frac{x_+ - 2x_a + x_-}{\Delta^2} \biggr]</math> |
<math>~\approx</math> |
<math>~ - ( 4g^2 - 6a^2 ) \biggl[\frac{x_+ - x_-}{2 \Delta} \biggr] - a \mathfrak{F}_\mathrm{core} x_a </math> |
|
<math>~\Rightarrow~~~ a (g^2 - a^2) \biggl[ \frac{x_+ }{\Delta^2} \biggr] + ( 4g^2 - 6a^2 ) \biggl[\frac{x_+ }{2 \Delta} \biggr] </math> |
<math>~\approx</math> |
<math>~a (g^2 - a^2) \biggl[ \frac{2x_a - x_-}{\Delta^2} \biggr] + ( 4g^2 - 6a^2 ) \biggl[\frac{x_-}{2 \Delta} \biggr] - a \mathfrak{F}_\mathrm{core} x_a </math> |
|
<math>~ \Rightarrow~~~x_+[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) ] </math> |
<math>~\approx</math> |
<math>~2a (g^2 - a^2) [ 2x_a - x_- ] + ( 4g^2 - 6a^2 ) [\Delta x_- ] - 2\Delta^2 a \mathfrak{F}_\mathrm{core} x_a </math> |
|
|
<math>~\approx</math> |
<math>~[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a + [ \Delta( 4g^2 - 6a^2 ) - 2a (g^2 - a^2)] x_- \, . </math> |
Now, at the very center of the configuration, <math>~(a = 0)</math>, we expect the function, <math>~x(\xi)</math>, to be symmetric; that is, we expect <math>~x_- = x_+</math>. So for this case alone, we have,
|
<math>~ x_+[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) - \Delta( 4g^2 - 6a^2 ) + 2a (g^2 - a^2)] </math> |
<math>~=</math> |
<math>~[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a </math> |
|
<math>~\Rightarrow~~~ x_+[2(g^2 - \cancelto{0}{a^2}) + 2(g^2 - \cancelto{0}{a^2})] </math> |
<math>~=</math> |
<math>~[4 (g^2 - \cancelto{0}{a^2}) - 2\Delta^2 \mathfrak{F}_\mathrm{core} ]x_a </math> |
|
<math>~\Rightarrow~~~ x_+ </math> |
<math>~=</math> |
<math>~\biggl[ 1 - \frac{\Delta^2 \mathfrak{F}_\mathrm{core}}{2g^2} \biggr]x_a \, . </math> |
For all other coordinate locations, <math>~a = \xi</math>, in the range, <math>~0 < \xi < 1</math>, we will use the general expression, namely,
|
<math>~ \Rightarrow~~~x_+ </math> |
<math>~\approx</math> |
<math>~\frac{[4a (g^2 - a^2) - 2\Delta^2 a \mathfrak{F}_\mathrm{core} ]x_a + [ \Delta( 4g^2 - 6a^2 ) - 2a (g^2 - a^2)] x_- }{[2a (g^2 - a^2) + \Delta( 4g^2 - 6a^2 ) ] } \, . </math> |
Keep in mind that, when we move across the interface at <math>~a = 1</math>, we want both the value of the function, <math>~x_q</math>, and its first derivative, <math>~x_q'</math>, to be the same as viewed from both the envelope and the core. In a numerical integration algorithm, it will be very straightforward to set the value of the eigenfunction at the interface. In order to properly handle the first derivative, I propose that we extend the core solution and evaluate the eigenfunction at one zone beyond the interface, and identify the values of the eigenfunction that straddles the interface as,
<math>~(x_-)_q</math> and <math>~(x_+)_q</math>.
Then define the slope of the eigenfunction at the interface by the expression,
| Slope at the Interface | |||
|
Integrating Outward Through the Envelope
From the LAWE for the envelope, we have,
|
<math>~a^2( 1 - q^3 a^3 ) x_a </math> |
<math>~=</math> |
<math>~ - ( 3 - 6q^3 a^3 ) a x_a' - [ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a \, . </math> |
Inserting the same finite-difference expressions for the first and second derivatives, we therefore have,
|
<math>~a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_+ - 2x_a + x_-}{\Delta^2} \biggr] </math> |
<math>~=</math> |
<math>~ - ( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_+ - x_-}{2 \Delta} \biggr] - [ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a </math> |
|
<math>~\Rightarrow ~~~ a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_+ }{\Delta^2} \biggr] + ( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_+ }{2 \Delta} \biggr] </math> |
<math>~=</math> |
<math>~ ( 3 - 6q^3 a^3 ) a \biggl[ \frac{x_-}{2 \Delta} \biggr] - a^2( 1 - q^3 a^3 ) \biggl[ \frac{x_- - 2x_a }{\Delta^2} \biggr] - [ q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a </math> |
|
<math>~\Rightarrow ~~~ x_+ [2a^2( 1 - q^3 a^3 ) + \Delta ( 3 - 6q^3 a^3 ) a ] </math> |
<math>~=</math> |
<math>~ [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] x_- + [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a </math> |
Now, at the interface (only), we need to relate <math>~x_-</math> to <math>~x_+</math> in such a way that the slope gives the proper value at the interface. Specifically, we need to set,
|
<math>~x_-</math> |
<math>~=</math> |
<math>~x_+ - 2\Delta (x_q') \, ,</math> |
where, <math>~x_q'</math> takes the value that was determined for the core. Hence, at the interface <math>~(a = 1)</math>, the first step into the envelope is special and demands that,
|
<math>~ x_+ [2a^2( 1 - q^3 a^3 ) + \Delta ( 3 - 6q^3 a^3 ) a ] </math> |
<math>~=</math> |
<math>~ [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] [x_+ - 2\Delta (x_q')] + [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a </math> |
|
<math>~\Rightarrow ~~~ x_+ [4a^2( 1 - q^3 a^3 ) ] </math> |
<math>~=</math> |
<math>~ [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] [- 2\Delta (x_q')] + [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a </math> |
|
|
<math>~=</math> |
<math>~ -2\Delta [ \Delta ( 3 - 6q^3 a^3 ) a - 2a^2( 1 - q^3 a^3 ) ] x_q' + [4a^2( 1 - q^3 a^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] x_a </math> |
|
and, setting, <math>~a = 1 ~~~~\Rightarrow ~~~ x_+ </math> |
<math>~=</math> |
<math>~ \frac{ 2\Delta [2( 1 - q^3 ) - \Delta ( 3 - 6q^3 ) ] x_q' + [4( 1 - q^3 ) - 2\Delta^2 ( q^3 \mathfrak{F}_\mathrm{env} -\alpha_e ) ] x_a }{ 4( 1 - q^3 ) } \, . </math> |
Varying the Oscillation Frequency
Approach
First, we fix <math>~q</math>, <math>~\gamma_e</math>, and <math>~\gamma_c</math>; in the example, here (as above) we choose: <math>~(q,\gamma_e,\gamma_c) = ( 0.6840119, 1.1940299, 1.845579)</math>. For this example, we will also retain the constraint, <math>~g^2 = \mathcal{B}</math>, in which case,
|
<math>~\frac{\rho_e}{\rho_c} = \frac{2q^3}{1+2q^3}</math> |
<math>~\approx</math> |
<math>~0.3902664 \, .</math> |
Next, we pick various values of the (square of the) dimensionless oscillation frequency, <math>~\sigma_c^2</math>, and, in order to ensure that the dimensional frequency in the envelope matches the dimensional frequency of the core, from each value we set,
|
<math>~\mathfrak{F}_\mathrm{core} </math> |
<math>~=</math> |
<math>~\frac{\sigma_c^2 + 8}{\gamma_c} - 6 \, ,</math> |
|
<math>~\mathfrak{F}_\mathrm{env} </math> |
<math>~=</math> |
<math>~\frac{1}{\gamma_e} \biggl[ \sigma_c^2 \biggl(\frac{\rho_e}{\rho_c} \biggr)^{-1} + 8\biggr]- 6 \, .</math> |
For the finite-difference algorithm, we divide the core — radial coordinate range, <math>~0 \le \xi \le 1</math> — into Ncore zones, and the envelope — radial coordinate range, <math>~1\le \xi \le 1/q</math> — into Nenv zones. This means that the spacing between successive radial zones in the core and envelope is, respectively,
|
<math>~\Delta_c \equiv \frac{1}{\mathrm{N}_\mathrm{core}}</math> |
and |
<math>~\Delta_e \equiv \frac{q^{-1} - 1}{\mathrm{N}_\mathrm{env}} \, .</math> |
Starting at the center of the configuration <math>~(\xi = 0)</math>, where we arbitrarily set the value of the eigenfunction to <math>~x_0 = 1</math>, the value of the eigenfunction at the first grid point away from the center <math>~(\xi = \Delta_c)</math> is,
|
<math>~ x_{k=1} </math> |
<math>~=</math> |
<math>~\biggl[ 1 - \frac{\Delta_c^2 \mathfrak{F}_\mathrm{core}}{2g^2} \biggr]x_0 \, . </math> |
Thereafter — moving out toward and just beyond the interface location <math>~(\xi = 1)</math>, the radial coordinate of each successive grid point is <math>~\xi_k = k\Delta_c</math>, and the numerically determined value of the eigenfunction at each successive grid point <math>~(k = 1 \rightarrow \mathrm{N}_\mathrm{core})</math> is,
|
<math>~ x_{k+1} </math> |
<math>~\approx</math> |
<math>~\frac{[4\xi_k (g^2 - \xi_k^2) - 2\Delta_c^2 \xi_k \mathfrak{F}_\mathrm{core} ]x_k + [ \Delta_c( 4g^2 - 6\xi_k^2 ) - 2\xi_k (g^2 - \xi_k^2)] x_{k-1} }{[2\xi_k (g^2 - \xi_k^2) + \Delta_c( 4g^2 - 6\xi_k^2 ) ] } \, . </math> |
Then, at the interface, which is associated with <math>~k = \mathrm{N}_\mathrm{core}</math>, we define the reference slope as,
|
<math>~x_q'</math> |
<math>~=</math> |
<math>~\frac{x_{k+1} - x_{k-1}}{2\Delta_c} \, .</math> |
Next, we move outward into the envelope, using the integer index, <math>~n = 1 \rightarrow \mathrm{N}_\mathrm{env}</math>, to label successive radial grid locations <math>~(\xi_n = 1 + n\Delta_e)</math>. Letting the value of the eigenfunction at the interface be represented by <math>~x_q</math>, at the first grid location outside the interface <math>~(\xi = 1 + \Delta_e)</math>, the value of the eigenfunction is,
|
<math align="right"> ~x_{n=1} </math> |
<math>~=</math> |
<math>~ \frac{ 2\Delta_e [2( 1 - q^3 ) - \Delta_e ( 3 - 6q^3 ) ] x_q' + [4( 1 - q^3 ) - 2\Delta_e^2 ( q^3 \mathfrak{F}_\mathrm{env} -\alpha_e ) ] x_q }{ 4( 1 - q^3 ) } \, . </math> |
Thereafter, moving outward through the envelope to the surface, the value of the eigenfunction at each successive grid location is,
|
<math>~ x_{n+1} </math> |
<math>~=</math> |
<math>~ \frac{[ \Delta_e ( 3 - 6q^3 \xi_n^3 ) \xi_n - 2\xi_n^2( 1 - q^3 \xi_n^3 ) ] x_{n-1} + [4\xi_n^2( 1 - q^3 \xi_n^3 ) - 2\Delta_e^2 ( q^3 \mathfrak{F}_\mathrm{env} \xi_n^3 -\alpha_e ) ] x_{n} }{ [2\xi_n^2( 1 - q^3 \xi_n^3 ) + \Delta_e ( 3 - 6q^3 \xi_n^3 ) \xi_n ] } \, . </math> |
TEST: We tested this finite-difference algorithm on a grid of resolution, <math>~\mathrm{N}_\mathrm{core} = \mathrm{N}_\mathrm{core} = 50</math>, by first setting <math>~\sigma_c^2 = 28.91158</math>. The resulting, numerically constructed eigenfunction matched to high accuracy the analytically generated eigenfunction shown, above, as Figure 1; see also, the middle image in the top panel of Figure 2. Representative values of the numerically determined eigenfunction, <math>~x(\xi)</math> at various discrete grid locations are provided in Table 1, along with the numerically determined value of the slope at the interface, <math>~x_q'</math>. At each grid location, the associated value of the dimensionless radius, <math>~r/R</math>, may be obtained by simply multiplying each tabulated value of <math>~\xi</math> by the parameter, <math>~q</math>.
|
Table 1: |
|||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||
| Core | Envelope | ||||||||||||||||||||||
|
|
||||||||||||||||||||||
| <math>~k</math> | <math>~\xi</math> | <math>~x</math> | <math>~n</math> | <math>~\xi</math> | <math>~x</math> | ||||||||||||||||||
| 0 | 0.00 | 1.000000 | 0 | 1.00 | -0.057649 | ||||||||||||||||||
| 1 | 0.02 | 0.997885 | 1 | 1.0092393 | -0.076955 | ||||||||||||||||||
| 2 | 0.04 | 0.997182 | 2 | 1.0184785 | -0.095792 | ||||||||||||||||||
| <math>~\vdots</math> | <math>~\vdots</math> | <math>~\vdots</math> | <math>~\vdots</math> | <math>~\vdots</math> | <math>~\vdots</math> | ||||||||||||||||||
| 49 | 0.98 | -0.015811 | 49 | 1.452724 | 0.466484 | ||||||||||||||||||
| 50 | 1.00 | -0.057649 | 50 | 1.461963 | 0.535957 | ||||||||||||||||||
| <math>~x_q' = -2.113043</math> | |||||||||||||||||||||||
Results
Motivated by Analytic21
Continuing with our analysis of the equilibrium model that is defined by the parameters, <math>~(q,\gamma_e,\gamma_c) = ( 0.6840119, 1.1940299, 1.845579)</math>, we have used the above-described numerical algorithm, to construct 26 different eigenfunctions that simultaneously satisfy the LAWE of the core and the LAWE of the envelope for 26 different values of <math>~\sigma_c^2</math> in the range, <math>~300 \ge \sigma_c^2 \ge 0</math>. The curve traced by a sequence of small circular markers (red = core; green = envelope) in the bottom panel of Figure 2 displays each of these numerically constructed eigenfunctions in succession — in order of decreasing values of <math>~\sigma_c^2</math> — in the form of a looped animation sequence. Also displayed in each frame of the animation, for reference, is the relevant value of <math>~\sigma_c^2</math>, as well as an unchanging, smooth, thin red/green curve that traces the analytically derived eigenfunction shown in Figure 1, for which <math>~\sigma_c^2 = 28.91158</math>.
Three frames from the animation sequence have been displayed side-by-side in the top panel of Figure 2. This image montage is presented, in part, to illustrate the degree to which our numerically generated eigenfunction matches the analytically generated eigenfunction in the specific case <math>~(\sigma_c^2 = 28.9)</math> for which we have been able to obtain an analytic solution to the combined/matched, core/envelope LAWEs.
Motivated by Analytic22
We have also numerically constructed an eigenfunction that matches our accompanying analytic Illustration22. In Figure 3, the numerically derived solution has been plotted on top of the analytically derived solution.
Motivated by Analytic31
We have also numerically constructed an eigenfunction that matches our accompanying analytic Illustration31. In Figure 4, the numerically derived solution has been plotted on top of the analytically derived solution.
Unconstrained LAWEs
Here we use the most general expressions for the pair of governing LAWEs; that is, we will not force <math>~g^2 = \mathcal{B}</math>. Drawing from our most general summary discussion, the LAWE for the core is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ (1 - \eta^2)\frac{d^2x}{d\eta^2} + ( 4 - 6\eta^2 ) \frac{1}{\eta} \cdot \frac{dx}{d\eta} + \mathfrak{F}_\mathrm{core} x \, . </math> |
where,
<math>~\eta \equiv \frac{\xi}{g} \, ,</math> and <math>~\mathfrak{F}_\mathrm{core} \equiv \frac{3\omega_\mathrm{core}^2}{2\pi G\gamma_c \rho_c} - 2\alpha_c = \frac{(\sigma_c^2 +8)}{\gamma_c} -6 \, ,</math>
and,
|
<math>~g^2</math> |
<math>~\equiv</math> |
<math> 1 + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_c} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, . </math> |
Hence, we may also write the core's LAWE as,
|
<math>~0</math> |
<math>~=</math> |
<math>~ (g^2 - \xi^2)\frac{d^2x}{d\xi^2} + ( 4g^2 - 6\xi^2 ) \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \mathfrak{F}_\mathrm{core} x \, , </math> |
and we should be able to numerically integrate from the center, outward through the core, exactly as described above.
Separately, the LAWE for the envelope is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl[ 1 + \frac{(g^2-\mathcal{B}) \xi}{\mathcal{A}} - \mathcal{D} \xi^3\biggr] \frac{d^2x}{d\xi^2} + \biggl\{ 3 + \frac{4(g^2-\mathcal{B}) \xi}{\mathcal{A}} - 6\mathcal{D} \xi^3 \biggr\} \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \mathcal{D} \mathfrak{F}_\mathrm{env} \xi^3 -\alpha_e \biggr]\frac{x}{\xi^2} \, , </math> |
where,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>~2\biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \, ; </math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math>~1 + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) - 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \, , </math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math>~\frac{1}{\mathcal{A}}\biggl( \frac{\rho_e}{\rho_c}\biggr)^2 = \biggl[ \frac{\rho_e/\rho_c}{2(1-\rho_e/\rho_c)} \biggr] \, , </math> |
|
<math>~\mathfrak{F}_\mathrm{env}</math> |
<math>~\equiv</math> |
<math>~\frac{3\omega^2_\mathrm{env}}{2\pi G \gamma_e \rho_e} - 2\alpha_e = \frac{1}{\gamma_e}\biggl[\frac{\sigma_c^2}{(\rho_e/\rho_c)} + 8\biggr] - 6 \, . </math> |
After defining the new parameter,
<math>~\mathcal{H} \equiv \frac{g^2 - \mathcal{B}}{\mathcal{A}} \, ,</math>
this LAWE for the envelope may be written as,
|
<math>~a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) x_a </math> |
<math>~=</math> |
<math>~ - ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a x_a' - [ \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a \, . </math> |
Inserting the same finite-difference expressions for the first and second derivatives, we therefore have,
|
<math>~a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )\biggl[ \frac{x_+ - 2x_a + x_-}{\Delta^2} \biggr] </math> |
<math>~=</math> |
<math>~ - ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a \biggl[ \frac{x_+ - x_-}{2 \Delta} \biggr] - [ \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a </math> |
|
<math>~\Rightarrow ~~~ a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )\biggl[ \frac{x_+ }{\Delta^2} \biggr] + ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a \biggl[ \frac{x_+ }{2 \Delta} \biggr] </math> |
<math>~=</math> |
<math>~ ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a \biggl[ \frac{x_-}{2 \Delta} \biggr] - a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )\biggl[ \frac{x_-}{\Delta^2} \biggr] - [ \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ]x_a + a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )\biggl[ \frac{2x_a }{\Delta^2} \biggr] </math> |
|
<math>~\Rightarrow ~~~x_+ [2 a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) + \Delta ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a ] </math> |
<math>~=</math> |
<math>~ x_- [ \Delta( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a - 2a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )] + x_a [ 4a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) - 2\Delta^2( \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] \, . </math> |
Now, at the interface (only), we need to relate <math>~x_-</math> to <math>~x_+</math> in such a way that the slope gives the proper value at the interface. Specifically, we need to set,
|
<math>~x_-</math> |
<math>~=</math> |
<math>~x_+ - 2\Delta (x_q') \, ,</math> |
where, <math>~x_q'</math> takes the value that was determined for the core. Hence, at the interface <math>~(a = 1)</math>, the first step into the envelope is special and demands that,
|
<math>~x_+ [2 a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) + \Delta ( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a ] </math> |
<math>~=</math> |
<math>~ [x_+ - 2\Delta (x_q')][ \Delta( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a - 2a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )] + x_a [ 4a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) - 2\Delta^2( \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] </math> |
|
<math>~\Rightarrow ~~~ x_+ [4 a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) ] </math> |
<math>~=</math> |
<math>~ - 2\Delta [ \Delta( 3 +4\mathcal{H}a - 6 \mathcal{D} a^3 ) a - 2a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 )] x_q' + x_a [ 4a^2( 1 + \mathcal{H}a - \mathcal{D} a^3 ) - 2\Delta^2( \mathcal{D} \mathfrak{F}_\mathrm{env} a^3 -\alpha_e ) ] </math> |
|
and, setting, <math>~a = 1 ~~~~\Rightarrow ~~~ x_+ </math> |
<math>~=</math> |
<math>~ \frac{ \Delta [ 2( 1 + \mathcal{H} - \mathcal{D} )- \Delta( 3 +4\mathcal{H} - 6 \mathcal{D} ) ] x_q' + x_a [ 2( 1 + \mathcal{H} - \mathcal{D} ) - \Delta^2( \mathcal{D} \mathfrak{F}_\mathrm{env} -\alpha_e ) ] }{ 2 ( 1 + \mathcal{H} - \mathcal{D} ) } \, . </math> |
Discussion
Conclusions
Initially, I was surprised to find that, by employing our above-described numerical algorithm, we were able to solve the combined/matched LAWEs for a continuum set — rather than a discrete set — of dimensionless oscillation frequencies, <math>~\sigma_c^2</math>. After all, I have been taught to believe that radial oscillation modes are obtained by solving an eigenvalue problem. After a bit of thought, I recognized that the continuum set of solutions has been obtained in the absence of a specified surface boundary condition. I suspect that the continuum of solutions can only be relevant to a real astrophysical problem after a physically meaningful surface boundary condition has been imposed; for example, a specification of the slope of the eigenfunction at the equilibrium configuration's surface. This should naturally reduce the continuum set to a discrete set of eigenvectors.
Watching the animation sequence reveals, for example, that as the value of <math>~\sigma_c^2</math> is reduced, the number of nodes inside the configuration is reduced, in a predictable, quantized fashion. At the same time — between each drop in the integer number of nodes — the slope of the eigenfunction at the surface <math>~(r/R = 1)</math> varies between large positive, and large negative values. Hence, we should be able to find a matched solution whose slope at the surface also matches any reasonably specified boundary condition.
Additional Possibilities
- We should be able to numerically identify a wide range of quantized radial modes of oscillation by specifying a physically reasonable surface slope then, for each successive quantum node count, tuning the choice of <math>~\sigma_c^2</math> until the desired slope has been encountered.
- It seems unlikely that any of our analytically derived eigenfunctions will happen to satisfy the specified boundary condition. The analytic functions have nevertheless proven to be useful in the sense that they provide a terrific check for the computational algorithm that, then, can be used to identify physically meaningful solutions numerically.
- Tie this new (numerical) technique into the associated discussion of the relationship between stability determinations via LAWEs and global free-energy considerations.
- The Figure 2 animation displays numerically determined solutions, <math>~x(r/R)</math>, to the combined/matching LAWEs only for non-negative values of <math>~\sigma_c^2</math>; these should be relevant only to stable radial oscillations. We should also see what can be learned from solutions associated with negative values of <math>~\sigma_c^2</math>, which may be relevant to unstable radial modes of oscillation.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |