Difference between revisions of "User:Tohline/SSC/Virial/Polytropes"
m (→Gravitational Potential Energy: Correct minor subscript error) |
|||
| (86 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
=Virial Equilibrium of Adiabatic Spheres= | =Virial Equilibrium of Adiabatic Spheres= | ||
Highlights of the rather detailed discussion presented below have been [[User:Tohline/SSC/Virial/PolytropesSummary|summarized in an accompanying chapter]] of this H_Book. | |||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
==Review== | ==Review== | ||
In an [[User:Tohline/SphericallySymmetricConfigurations/Virial#Virial_Equilibrium_of_Spherically_Symmetric_Configurations|introductory discussion]] of the virial equilibrium structure of spherically symmetric configurations | ===Adopted Normalizations=== | ||
In an [[User:Tohline/SphericallySymmetricConfigurations/Virial#Virial_Equilibrium_of_Spherically_Symmetric_Configurations|introductory discussion]] of the virial equilibrium structure of spherically symmetric configurations, we adopted the following physical parameter normalizations for adiabatic systems. | |||
<div align="center"> | <div align="center"> | ||
< | <table border="1" align="center" cellpadding="5"> | ||
< | <tr><th align="center" colspan="1"> | ||
Adopted Normalizations for Adiabatic Systems | |||
< | </th></tr> | ||
< | <tr><td align="center"> | ||
</ | <table border="0" cellpadding="5" align="center"> | ||
< | |||
< | |||
<table border="0" cellpadding="5"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~R_\mathrm{norm}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 26: | Line 24: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>\frac{ | <math>~\biggl[ \biggl( \frac{G}{K} \biggr) M_\mathrm{tot}^{2-\gamma_g} \biggr]^{1/(4-3\gamma_g)} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 32: | Line 30: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P_\mathrm{norm}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 38: | Line 36: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\biggl[ \frac{K^4}{G^{3\gamma_g} M_\mathrm{tot}^{2\gamma_g}} \biggr]^{1/(4-3\gamma_g)} </math> | ||
\biggl | </td> | ||
</ | </tr> | ||
<tr> | |||
<td align="center" colspan="3"> | |||
---- | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 46: | Line 48: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~E_\mathrm{norm}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 52: | Line 54: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ P_\mathrm{norm} R_\mathrm{norm}^3 = | ||
1 \ | \biggl[ KG^{3(1-\gamma_g)}M_\mathrm{tot}^{6-5\gamma_g} \biggr]^{1/(4-3\gamma_g)} </math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 60: | Line 61: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\rho_\mathrm{norm}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 66: | Line 67: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\frac{3M_\mathrm{tot}}{4\pi R_\mathrm{norm}^3} | ||
\frac{3 | = \frac{3}{4\pi} \biggl[ \frac{K^3}{G^3 M_\mathrm{tot}^2} \biggr]^{1/(4-3\gamma_g )} </math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 74: | Line 74: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~c^2_\mathrm{norm}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 80: | Line 80: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\frac{P_\mathrm{norm}}{\rho_\mathrm{norm}} | ||
= \frac{4\pi}{3} \biggl[ \frac{K}{(G^3 M_\mathrm{tot}^2)^{\gamma_g-1}} \biggr]^{1/(4-3\gamma_g )} </math> | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
== | ===Virial Equilibrium=== | ||
Also in our introductory discussion — see especially the section titled, [[User:Tohline/SphericallySymmetricConfigurations/Virial#Energy_Extrema|''Energy Extrema'']] — we deduced that an adiabatic system's dimensionless equilibrium radius, | |||
<div align="center"> | <div align="center"> | ||
<math> | <math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \, ,</math> | ||
</math> | |||
</div> | </div> | ||
is given by the root(s) of the following equation: | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
3 B\chi_\mathrm{eq}^{3 -3\gamma_g} | 2C \chi_\mathrm{eq}^{-2} + ~3 B\chi_\mathrm{eq}^{3 -3\gamma_g} -~3A\chi_\mathrm{eq}^{-1} -~ 3D \chi_\mathrm{eq}^3 = 0 \, , | ||
</math> | </math> | ||
</div> | </div> | ||
where the definitions of the various coefficients are, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5"> | ||
<tr> | |||
<td align="right"> | |||
<math>~A</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~B</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{4\pi}{3} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} | |||
\cdot \mathfrak{f}_A | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 133: | Line 143: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{4\pi}{3} | |||
\biggl[ \frac{ | \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} | ||
\cdot \mathfrak{f}_A \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~C</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{3\cdot 5}{2^4 \pi} \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \cdot \frac{\mathfrak{f}_T}{\mathfrak{f}_M} \, , | |||
\ | </math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~D</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 156: | Line 178: | ||
</table> | </table> | ||
</div> | </div> | ||
(The [[User:Tohline/SphericallySymmetricConfigurations/Virial#Structural_Form_Factors|dimensionless structural form factors]], <math>~\mathfrak{f}_i,</math> that appear in these expressions are defined ''for isolated polytropes'' in our accompanying introductory discussion and are [[User:Tohline/SSC/Virial/Polytropes#Role_of_Structural_Form_Factors|discussed further, below]].) Once the pressure exerted by the external medium (<math>~P_e</math>), and the configuration's mass (<math>~M_\mathrm{tot}</math>), angular momentum (<math>~J</math>), and specific entropy (via <math>~K</math>) have been specified, the values of all of the coefficients are known and <math>~\chi_\mathrm{eq}</math> can be determined. | |||
==Isolated Nonrotating Adiabatic Configuration== | |||
For a nonrotating configuration <math>~(C=J=0)</math> that is not influenced by the effects of a bounding external medium <math>~(D=P_e = 0)</math>, the statement of virial equilibrium is, | |||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
3 B\chi_\mathrm{eq}^{3 -3\gamma_g} -~3A\chi_\mathrm{eq}^{-1} = 0 \, . | |||
</math> | </math> | ||
</div> | </div> | ||
Hence, one equilibrium state exists for each value of <math>~\gamma_g</math> and it occurs where, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{\ | <math>~\chi_\mathrm{eq}^{4-3\gamma_g} = \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{4-3\gamma_g} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 184: | Line 202: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{A}{B} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
<div align="center"> | <div align="center" id="TwoPointsOfView"> | ||
<table border=" | <table border="1" width="100%" cellpadding="8"> | ||
<tr> | |||
<th align="center" colspan="2"> | |||
Two Points of View | |||
</th> | |||
</tr> | |||
<tr> | <tr> | ||
<td align=" | <td align="center" colspan="1"> | ||
<math>~ | In terms of <math>~K</math> and <math>~M_\mathrm{limit} ~(= M_\mathrm{tot})</math> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align=" | <td align="center" colspan="1"> | ||
<math>~ \ | In terms of <math>~P_c</math> and <math>~M_\mathrm{limit} ~(= M_\mathrm{tot})</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<td align="center" colspan="1"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~- | <math>~\chi_\mathrm{eq}^{4-3\gamma_g}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 219: | Line 240: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\biggl\{ | |||
\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\times | |||
\biggl\{ | |||
\frac{3}{4\pi} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{-{\gamma_g}} | |||
\cdot \frac{1}{\mathfrak{f}_A} | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow~~~R_\mathrm{eq}^{4-3\gamma_g}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 252: | Line 275: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{4\pi}{3\cdot 5} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{2-{\gamma_g}} | |||
\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A} \biggl[ | |||
\frac{GM_\mathrm{tot}^{2-\gamma_g}}{K} \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 258: | Line 286: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>\Rightarrow | <math>\Rightarrow ~~\frac{KR_\mathrm{eq}^{4-3\gamma_g}}{GM_\mathrm{limit}^{2-\gamma_g}}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 264: | Line 292: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{1}{5} \biggl( \frac{4\pi}{3} \biggr)^{\gamma_g-1} \frac{\mathfrak{f}_W}{\mathfrak{f}_A \mathfrak{f}_M^{2-\gamma_g}} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
— — — — — — or, | |||
inverted and setting <math>~\gamma_g = 1 + 1/n</math> — — — — — — | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center" colspan="3"> | ||
<math>~ | <math>~ | ||
4\pi \biggl( \frac{G}{K} \biggr)^n M_\mathrm{limit}^{n-1} R_\mathrm{eq}^{3-n} | |||
= | |||
\biggl( \frac{5 \mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr)^n \frac{3}{\mathfrak{f}_M} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
<td align="center" colspan="1"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}^{4-3\gamma_g}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 282: | Line 329: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\biggl\{ | |||
\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\times | |||
\biggl\{ | |||
\frac{3} {4\pi} | |||
\biggl[ \biggl( \frac{P_\mathrm{norm}}{P_c} \biggr)\chi^{-3\gamma} \biggr]_\mathrm{eq} | |||
\cdot \frac{1}{\mathfrak{f}_A} | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 309: | Line 358: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~\chi_\mathrm{eq}^{4}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 315: | Line 364: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 | |||
\biggl( \frac{P_\mathrm{norm}}{P_c} \biggr) | |||
\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \cdot \mathfrak{f}_M^2} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow~~~\frac{P_c R_\mathrm{eq}^{4}}{P_\mathrm{norm} R_\mathrm{norm}^4} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{limit}} \biggr)^{2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 334: | Line 383: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{3}{20\pi} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \cdot \mathfrak{f}_M^2} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ \ | <math>~\Rightarrow~~~\frac{P_c R_\mathrm{eq}^{4}}{G M_\mathrm{limit}^2} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 352: | Line 397: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{3}{20\pi} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \cdot \mathfrak{f}_M^2} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
According to the solution shown in the left-hand column, for fluid with a given specify entropy content, the equilibrium mass-radius relationship for adiabatic configurations is, | |||
<div align="center"> | |||
<math> | |||
M_\mathrm{tot}^{(\gamma_g - 2)} \propto R_\mathrm{eq}^{(3\gamma_g -4)} \, . | |||
</math> | |||
</div> | |||
We see that, for <math>~\gamma_g=2</math>, the equilibrium radius depends only on the specific entropy of the gas and is independent of the configuration's mass. Conversely, for <math>~\gamma_g = 4/3</math>, the mass of the configuration is independent of the radius. For <math>~\gamma_g > 2</math> or <math>~\gamma_g < 4/3</math>, configurations with larger mass (but the same specific entropy) have larger equilibrium radii. However, for <math>~\gamma_g</math> in the range, <math>~2 > \gamma_g > 4/3</math>, configurations with larger mass have smaller equilibrium radii. (Note that the related result for [[User:Tohline/SSC/Virial/Isothermal#Virial_Equilibrium_of_Isothermal_Spheres|isothermal configurations]] can be obtained by setting <math>~\gamma_g = 1</math> in this adiabatic solution, because <math>~K = c_s^2</math> when <math>~\gamma_g = 1</math>.) | |||
==Role of Structural Form Factors== | |||
When employing a virial analysis to determine the radius of an equilibrium configuration, it is customary to set the structural form factors, <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_A</math>, to unity and accept that the expression derived for <math>~R_\mathrm{eq}</math> is an estimate of the configuration's radius that is good to within a factor of order unity. As has been demonstrated in our [[User:Tohline/SSC/VirialEquilibrium/UniformDensity#Comparison_with_Detailed_Force-Balance_Model|related discussion of the equilibrium of uniform-density spheres]], these form factors can be evaluated if/when the internal structural profile of an equilibrium configuration is known from a complementary detailed force-balance analysis. In the case being discussed here of isolated, spherical polytropes, [[User:Tohline/SSC/Structure/Polytropes#Lane-Emden_Equation|solutions to the]], | |||
<div align="center"> | |||
<span id="LaneEmdenEquation"><font color="#770000">'''Lane-Emden Equation'''</font></span> | |||
<br /> | |||
{{User:Tohline/Math/EQ_SSLaneEmden01}} | |||
</div> | |||
can provide the desired internal structural information. Here we draw on [[User:Tohline/Appendix/References|Chandrasekhar's [C67]]] discussion of the structure of spherical polytropes to show precisely how our structural form factors can be expressed in terms of the Lane-Emden function, <math>~\Theta_H</math>, dimensionless radial coordinate, <math>~\xi</math>, and the function derivative, <math>~\Theta^' = d\Theta_H/d\xi</math>. | |||
===Mass=== | |||
We note, first, that [[User:Tohline/Appendix/References|Chandrasekhar [C67]]] — see his Equation (78) on p. 99 — presents the following expression for the mean-to-central density ratio: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~\frac{\bar\rho}{\rho_c}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 385: | Line 438: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\xi_1} \, ,</math> | ||
\frac{ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where the notation at the bottom of the closing square bracket means that everything inside the square brackets should be, "evaluated at the surface of the configuration," that is, at the radial location, <math>~\xi_1</math>, where the Lane-Emden function, <math>~\Theta_H(\xi)</math>, first goes to zero. But, as we pointed out when [[User:Tohline/SphericallySymmetricConfigurations/Virial#Structural_Form_Factors|defining the structural form factors]], the form factor associated with the configuration mass, <math>~\mathfrak{f}_M</math>, is equivalent to the mean-to-central density ratio. We conclude, therefore, that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~\mathfrak{f}_M</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 399: | Line 454: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\xi_1} \, .</math> | ||
</td> | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
</div> | |||
===Gravitational Potential Energy=== | |||
Second, we note that [[User:Tohline/Appendix/References|Chandrasekhar's [C67]]] expression for the gravitational potential energy — see his Equation (90), p. 101 — is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~-W</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 413: | Line 473: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\frac{3}{5-n} \biggl( \frac{GM^2}{R} \biggr) \, ,</math> | ||
\frac{3 | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
whereas our analogous expression is, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~-W_\mathrm{grav}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 433: | Line 489: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
We conclude, therefore, that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{5}{5-n} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>\Rightarrow ~~~~\mathfrak{f}_W </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 465: | Line 518: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{3}{ | <math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\xi_1} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 471: | Line 524: | ||
</div> | </div> | ||
=== | ===Mass-Radius Relationship=== | ||
Third, [[User:Tohline/Appendix/References|Chandrasekhar [C67]]] shows — see his Equation (72), p. 98 — that the general mass-radius relationship for isolated spherical polytropes is, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~GM^{(n-1)/n} R^{(3-n)/n}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 486: | Line 537: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
~\frac{ | ~\frac{(n+1)K}{(4\pi)^{1/n}} \biggl[ - \xi^{(n+1)/(n-1)} \frac{d\Theta_H}{d\xi} \biggr]^{(n-1)/n}_{\xi=\xi_1} \, , | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 492: | Line 543: | ||
</table> | </table> | ||
</div> | </div> | ||
which we choose to rewrite as, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 498: | Line 549: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R^{(3-n)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 505: | Line 556: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
~ | ~(n+1)^n\biggl[ \xi^{(n+1)} (-\Theta^')^{(n-1)}\biggr]_{\xi=\xi_1} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 513: | Line 563: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 520: | Line 570: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
- \biggl( \frac{\xi}{\Theta^'} \biggr)_{\xi=\xi_1} \biggl[ (n+1) \xi ~(-\Theta^') \biggr]^n_{\xi=\xi_1} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 526: | Line 576: | ||
</table> | </table> | ||
</div> | </div> | ||
By comparison, the expression for the equilibrium radius that has been derived, above, from an analysis of extrema in the free energy function — specifically, see the last expression in the left-hand column of the [[User:Tohline/SSC/Virial/Polytropes#TwoPointsOfView|table titled "Two Points of View"]] — we obtain, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~4\pi \biggl( \frac{G}{ | <math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R_\mathrm{eq}^{(3-n)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 540: | Line 589: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
~3 \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M | ~\frac{3}{\mathfrak{f}_M} \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr)^n \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Hence, it appears as though, quite generally, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~ \frac{1}{\mathfrak{f}_M} \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr)^n </math> | ||
\biggl( \frac{ | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 555: | Line 607: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
- \biggl( \frac{\xi}{3\Theta^'} \biggr)_{\xi=\xi_1} \biggl[ (n+1) \xi ~(-\Theta^') \biggr]^n_{\xi=\xi_1} \, . | |||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 570: | Line 613: | ||
</table> | </table> | ||
</div> | </div> | ||
Or, taking into account the expressions for <math>~\mathfrak{f}_M</math> and <math>~\mathfrak{f}_W</math> that have just been uncovered, we conclude that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{\mathfrak{f} | <math>~ \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 581: | Line 625: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math> | ||
\biggl[ (n+1) \xi ~(-\Theta^') \biggr]_{\xi=\xi_1} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right" | <td align="right"> | ||
<math>\Rightarrow ~~~~ \frac{\mathfrak{f}_A}{\mathfrak{f}_W} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | <math> | ||
\frac{(n+1) }{3\cdot 5} ~\xi_1^2 \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>\Rightarrow ~~~~ \mathfrak{f}_A </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 614: | Line 653: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
</td> | \frac{(n+1) }{3\cdot 5} ~\xi_1^2 \biggl\{ \frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\xi_1} \biggr\}\, . | ||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 630: | Line 667: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math> | ||
\frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\xi_1} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
===Central Pressure=== | |||
It is also worth pointing out that [[User:Tohline/Appendix/References|Chandrasekhar [C67]]] — see his Equations (80) & (81), p. 99 — introduces a dimensionless structural form factor, <math>~W_n</math>, for the central pressure via the expression, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P_c</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 646: | Line 687: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~W_n \biggl( \frac{GM^2}{R^4} \biggr) \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
and demonstrates that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\frac{1}{W_n}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~4\pi (n+1) \biggl[ \Theta^' \biggr]^2_{\xi_1} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
It is therefore clear that a spherical polytrope's central pressure is expressible in terms of our structural form factor, <math>~\mathfrak{f}_A</math>, as, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P_c</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 678: | Line 719: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~(n | <math>~\frac{3}{4\pi (5-n)} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) \frac{1}{\mathfrak{f}_A} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Hence, | |||
<!-- (August 2015) REMOVE NEXT FEW LINES, AS CONNECTION WITH MEAN PRESSURE IS UNJUSTIFIED ... | |||
Looking back at our [[User:Tohline/SphericallySymmetricConfigurations/Virial#FormFactors|original definition of the structural form factors]], we note that, | |||
<div align="center"> | |||
<math>\mathfrak{f}_A = \biggl( \frac{\bar{P}}{P_c} \biggr)_\mathrm{eq} \, .</math> | |||
</div> | |||
Hence, this last equilibrium relation can be rewritten as, | |||
<div align="center"> | <div align="center"> | ||
< | <math> \frac{\bar{P} R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} = \frac{3}{4\pi (5-n)} \, .</math> | ||
</div> | |||
END DELETION --> | |||
===Alternate Derivation of Gravitational Potential Energy=== | |||
<!-- BEGINNING OF DELETION: The following subsubsection is redundant, now that the "Two Points of View" table has been included. | |||
====Central Pressure==== | |||
As is pointed out, above, in our [[User:Tohline/SSC/Virial/Polytropes#Mass-Radius_Relationship|discussion of the mass-radius relationship]], the expression for the equilibrium radius that has been derived from our analysis of extrema in the free energy function can be written as, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R_\mathrm{eq}^{(3-n)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 695: | Line 752: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math> | ||
~\frac{3}{\mathfrak{f}_M} \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr)^n \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Via the polytropic equation of state, we can relate <math>~K</math> to the central pressure as follows: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~P_c</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 707: | Line 771: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math> | ||
~K \rho_c^{1+1/n} = K \bar\rho^{1+1/n} \biggl( \frac{\rho_c}{\bar\rho} \biggr)^{1+1/n} | |||
= K \biggl[ \frac{3M_\mathrm{tot}}{4\pi R_\mathrm{eq}^3} \biggr]^{(n+1)/n} \biggl( \frac{1}{\mathfrak{f}_M} \biggr)^{(n+1)/n} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 716: | Line 780: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>\Rightarrow ~~~~ K^{n}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 722: | Line 786: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\ | P_c^{n} \biggl[ \frac{4\pi R_\mathrm{eq}^3}{3M_\mathrm{tot}} \biggr]^{(n+1)} \mathfrak{f}_M^{(n+1)} \, . | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Hence, in the mass-radius relationship we can replace <math>~K</math> with this expression to obtain, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~4\pi \biggl( \frac{G}{P_c}\biggr)^n M^{(n-1)} R_\mathrm{eq}^{(3-n)} | |||
\biggl[ \frac{3M_\mathrm{tot}}{4\pi R_\mathrm{eq}^3} \biggr]^{(n+1)}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 737: | Line 806: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math> | ||
\frac{ | ~3 \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M^2}{\mathfrak{f}_W} \biggr)^n | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 746: | Line 814: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>\Rightarrow ~~~~ \biggl( \frac{G M_\mathrm{tot}^2}{P_c R_\mathrm{eq}^4}\biggr)^n | |||
\biggl( \frac{3}{4\pi } \biggr)^{n}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 752: | Line 821: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math> | ||
~\biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M^2}{\mathfrak{f}_W} \biggr)^n | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right" | <td align="right" colspan="3"> | ||
<math> | |||
\Rightarrow ~~~~ P_c = \frac{3 }{20\pi }\biggl( \frac{G M_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) | |||
\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \mathfrak{f}_M^2} \, . | |||
<math>~= | </math> | ||
\ | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Now, from our above [[User:Tohline/SSC/Virial/Polytropes#Gravitational_Potential_Energy|examination of the expression for the gravitational potential energy]], we know that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 786: | Line 848: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{5}{5-n} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Hence, our expression for the central pressure becomes, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | |||
<td align="right" colspan="3"> | |||
<math> | |||
~P_c = \frac{3 }{4\pi (5-n)}\biggl( \frac{G M_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) | |||
\cdot \frac{1}{\mathfrak{f}_A } \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
As it should, this precisely matches [[User:Tohline/SSC/Virial/Polytropes#Central_Pressure|the expression that we derived, above]], starting from [[User:Tohline/Appendix/References|Chandrasekhar's [C67]]] presentation. | |||
====Gravitational Potential Energy==== | |||
END OF DELETION --> | |||
As has been [[User:Tohline/SphericallySymmetricConfigurations/Virial#AlternateGravPotEnergy|discussed elsewhere]], we have learned from [[User:Tohline/Appendix/References|Chandrasekhar's discussion of polytropic spheres [C67]]] — see his Equation (16), p. 64 — that if a spherically symmetric system is in hydrostatic balance, the total gravitational potential energy can be obtained from the following integral: | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~W_\mathrm{grav}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 802: | Line 884: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac{ | <math>~ + \frac{1}{2} \int_0^R \Phi(r) dm \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Using "[[User:Tohline/SphericallySymmetricConfigurations/SolutionStrategies#Technique_3|technique #3]]" to solve the differential equation that governs the statement of hydrostatic balance, we know that in any polytropic sphere, <math>~\Phi(r)</math> is related to the configuration's radial enthalpy profile, <math>~H(r)</math>, via the algebraic expression, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Phi(r) + H(r)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 819: | Line 900: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~C_B \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where, <math>~C_B</math>, is an integration constant. At the surface of the equilibrium configuration, <math>~H = 0</math> and <math>~\Phi = - GM_\mathrm{tot}/R_\mathrm{eq}</math>, so the integration constant is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~C_B</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 833: | Line 916: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
which implies, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>\ | <math>~\Phi(r) </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 846: | Line 932: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ - H(r) - \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Now, from [[User:Tohline/SR#Barotropic_Structure|our general discussion of barotropic relations]], we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | <math>~H(r)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 858: | Line 948: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~(n+1) \frac{P(r)}{\rho(r)} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Hence, | |||
<div align="center"> | <div align="center"> | ||
<math> | <table border="0" cellpadding="5" align="center"> | ||
(1 | <tr> | ||
</ | <td align="right"> | ||
<math>~-\Phi(r)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(n+1) \frac{P(r)}{\rho(r)} + \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
and, | |||
<div align="center"> | <div align="center"> | ||
< | <table border="0" cellpadding="5"> | ||
= | <tr> | ||
<td align="right"> | |||
< | <math>~W_\mathrm{grav}</math> | ||
<math> | </td> | ||
<td align="center"> | |||
</math> | <math>~=</math> | ||
</ | </td> | ||
<td align="left"> | |||
<math>~ - \frac{1}{2} \int_0^R \biggl[ (n+1) \frac{P(r)}{\rho(r)} + \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \biggr] 4\pi \rho(r) r^2 dr </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
< | | ||
</td> | |||
<td align="center"> | |||
</ | <math>~=</math> | ||
< | </td> | ||
<td align="left"> | |||
<math>~ - 2\pi \biggl\{ | |||
<math> | (n+1) \int_0^R P(r) r^2 dr | ||
+ \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \int_0^R \rho(r) r^2 dr | |||
</math> | \biggr\} </math> | ||
</ | </td> | ||
</tr> | |||
< | |||
<math> | |||
\ | |||
<tr> | |||
< | <td align="right"> | ||
<math> | | ||
\ | </td> | ||
</math> | <td align="center"> | ||
</ | <math>~=</math> | ||
</td> | |||
< | <td align="left"> | ||
<math> | <math>~ - 2\pi \biggl\{ | ||
1 \ | \frac{1}{3} (n+1)P_c R_\mathrm{eq}^3 \int_0^1 3\biggl[ \frac{P(x)}{P_c} \biggr] x^2 dx | ||
</ | + \frac{GM_\mathrm{tot}}{3R_\mathrm{eq}} \biggl( \rho_c R_\mathrm{eq}^3 \biggr) \int_0^1 3 \biggl[ \frac{\rho(x)}{\rho_c} \biggr] x^2 dx | ||
\biggr\} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - 2\pi \biggl\{ | |||
\frac{1}{3} (n+1)P_c R_\mathrm{eq}^3 \mathfrak{f}_A | |||
+ \frac{GM_\mathrm{tot}}{3R_\mathrm{eq}} \biggl( \rho_c R_\mathrm{eq}^3 \biggr) \mathfrak{f}_M | |||
\biggr\} </math> | |||
</td> | |||
</tr> | |||
< | <tr> | ||
<td align="right"> | |||
| |||
</ | </td> | ||
<td align="center"> | |||
< | <math>~=</math> | ||
< | </td> | ||
< | <td align="left"> | ||
<td align=" | <math>~ - \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggl\{ | ||
\frac{2\pi}{3} (n+1) \biggl[ \frac{P_c R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} \biggr] \mathfrak{f}_A | |||
+ \frac{1}{2} \biggl[ \frac{4\pi \rho_c R_\mathrm{eq}^3}{3M_\mathrm{tot}} \biggr] \mathfrak{f}_M | |||
\biggr\} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
\ | | ||
</math> | </td> | ||
</ | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \frac{1}{2} \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggl\{ | |||
<td | \frac{4\pi}{3} (n+1) \biggl[ \frac{P_c R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} \biggr] \mathfrak{f}_A | ||
+ 1 | |||
\biggr\} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
We now recall two earlier expressions that show the role that our structural form factors play in the evaluation of <math>~W_\mathrm{grav}</math> and <math>~P_c</math>, namely, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~W_\mathrm{grav}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggr) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_c</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{3 }{20\pi }\biggl( \frac{G M_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) | |||
\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \mathfrak{f}_M^2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Plugging these into our newly derived expression for the gravitational potential energy gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~- \frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \frac{1}{2} \biggl\{ | |||
\frac{4\pi}{3} (n+1) \biggl[ \frac{3 }{20\pi }\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \mathfrak{f}_M^2} \biggr] \mathfrak{f}_A | |||
+ 1 \biggr\} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\Rightarrow ~~~~ (2\cdot 3) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(n+1) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} + 5 </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\Rightarrow ~~~~ (5 - n) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 5 </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\Rightarrow ~~~~ \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{5}{5-n} \, . </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
As it should, this agrees with the expression for the ratio, <math>\mathfrak{f}_W/\mathfrak{f}_M^2</math>, that was [[User:Tohline/SSC/Virial/Polytropes#Gravitational_Potential_Energy|derived in our above discussion of the gravitational potential energy]]. | |||
===Summary=== | |||
In summary, expressions for the three structural form factors associated with isolated, spherically symmetric polytropes are as follows: | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr><th align="center" colspan="1"> | |||
Structural Form Factors for <font color="red">Isolated</font> Polytropes | |||
</th></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{f}_M</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\xi_1} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\mathfrak{f}_W </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\xi_1} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\mathfrak{f}_A </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\xi_1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Nonrotating Adiabatic Configuration Embedded in an External Medium== | |||
For a nonrotating configuration <math>~(C=J=0)</math> that is embedded in, and is influenced by the pressure <math>~P_e</math> of, an external medium, the statement of virial equilibrium is, | |||
<div align="center"> | |||
<math> | |||
3 B\chi_\mathrm{eq}^{3 -3\gamma_g} -~3A\chi_\mathrm{eq}^{-1} -~ 3D\chi_\mathrm{eq}^3 = 0 \, . | |||
</math> | |||
</div> | |||
====Solution Expressed in Terms of K and M (Whitworth's 1981 Relation)==== | |||
This is precisely the same condition that derives from setting equation (3) to zero in [http://adsabs.harvard.edu/abs/1981MNRAS.195..967W Whitworth's] (1981, MNRAS, 195, 967) discussion of the ''Global Gravitational Stability for One-dimensional Polytropes''. The overlap with Whitworth's narative is clearer after introducing the algebraic expressions for the coefficients <math>~A</math>, <math>~B</math>, and <math>~D</math>, to obtain, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~4\pi \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^3 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} | |||
\frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot \chi_\mathrm{eq}^{3 -3\gamma_g} | |||
~-~\frac{3}{5} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \cdot \chi_\mathrm{eq}^{-1} \, ;</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
dividing the equation through by <math>~(4\pi \chi_\mathrm{eq}^3/P_\mathrm{norm})</math>, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_e </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~P_\mathrm{norm} \biggl[ \biggl( \frac{3}{4\pi} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} | |||
\cdot \chi_\mathrm{eq}^{-3\gamma_g} ~- \biggl(\frac{3}{20\pi} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 | |||
\frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \cdot \chi_\mathrm{eq}^{-4} \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~P_\mathrm{norm} R_\mathrm{norm}^4\biggl[ \biggl( \frac{3}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} | |||
\frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot R_\mathrm{norm}^{3\gamma_g-4} | |||
- \biggl(\frac{3}{20\pi R_\mathrm{eq}^4} \biggr)\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \biggr] \, ;</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and inserting expressions for the [[User:Tohline/SphericallySymmetricConfigurations/Virial#Normalizations|parameter normalizations]] as defined in our accompanying [[User:Tohline/SphericallySymmetricConfigurations/Virial#Virial_Equilibrium_of_Spherically_Symmetric_Configurations|introductory discussion]] to obtain, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_e </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~GM_\mathrm{tot}^2\biggl[ \biggl( \frac{3}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} | |||
\frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot \frac{K M_\mathrm{tot}^{\gamma_g-2}}{G} | |||
- \biggl(\frac{3}{20\pi R_\mathrm{eq}^4} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} | |||
- \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
If the structural form factors are set equal to unity, this exactly matches equation (5) of [http://adsabs.harvard.edu/abs/1981MNRAS.195..967W Whitworth], which reads: | |||
<div align="center"> | |||
<table border="1" cellpadding="5" width="80%"> | |||
<tr><td align="center"> | |||
Equation and accompanying sentence extracted without modification from p. 970 of [http://adsabs.harvard.edu/abs/1981MNRAS.195..967W Whitworth (1981)]<p></p> | |||
"''Global Gravitational Stability for One-dimensional Polytropes''"<p></p> | |||
Monthly Notices of the Royal Astronomical Society, vol. 195, pp. 967-977 © Royal Astronomical Society | |||
</td></tr> | |||
<tr> | |||
<td align="center"> | |||
<!-- [[File:Whitworth1981Eq5.jpg|500px|center|Whitworth (1981, MNRAS, 195, 967)]] --> | |||
[[Image:AAAwaiting01.png|400px|center|Whitworth (1981) Eq. 5]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Notice that, when <math>~P_e \rightarrow 0</math>, this expression reduces to the solution we obtained for an isolated polytrope, expressed in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math> (see the left-hand column of our [[User:Tohline/SSC/Virial/Polytropes#TwoPointsOfView|table titled "Two Points of View"]]). | |||
====Solution Expressed in Terms of M and Central Pressure==== | |||
Beginning again with the [[User:Tohline/SSC/Virial/Polytropes#Nonrotating_Adiabatic_Configuration_Embedded_in_an_External_Medium|relevant statement of virial equilibrium]], namely, | |||
<div align="center"> | |||
<math> | |||
A = B\chi_\mathrm{eq}^{4 -3\gamma_g} -~ D\chi_\mathrm{eq}^4 \, , | |||
</math> | |||
</div> | |||
but adopting the alternate expression for the coefficient, <math>~B</math>, [[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium|given above]], that is, | |||
<div align="center"> | |||
<math> | |||
B = \frac{4\pi}{3} | |||
\biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} | |||
\cdot \mathfrak{f}_A \, , | |||
</math> | |||
</div> | |||
we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \mathfrak{f}_A | |||
\cdot \chi_\mathrm{eq}^{4 -3\gamma_g} | |||
-~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \chi_\mathrm{eq}^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\frac{3}{20\pi} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \mathfrak{f}_A -~ \frac{P_e}{P_\mathrm{norm}} \biggr] \chi_\mathrm{eq}^4 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \mathfrak{f}_A P_c -~ P_e\biggr] \frac{R_\mathrm{eq}^4}{G M_\mathrm{tot}^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\Rightarrow ~~~ \frac{3}{20\pi} \biggl( \frac{G M_\mathrm{limit}^2}{R_\mathrm{eq}^4}\biggr) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{f}_A P_c -~ P_e \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Again notice that, when <math>~P_e \rightarrow 0</math>, this expression reduces to the solution we obtained for an isolated polytrope, but this time expressed in terms of <math>~P_c</math> and <math>~M_\mathrm{limit}</math> (see the right-hand column of our [[User:Tohline/SSC/Virial/Polytropes#TwoPointsOfView|table titled "Two Points of View"]]). | |||
====Contrast with Detailed Force-Balanced Solution==== | |||
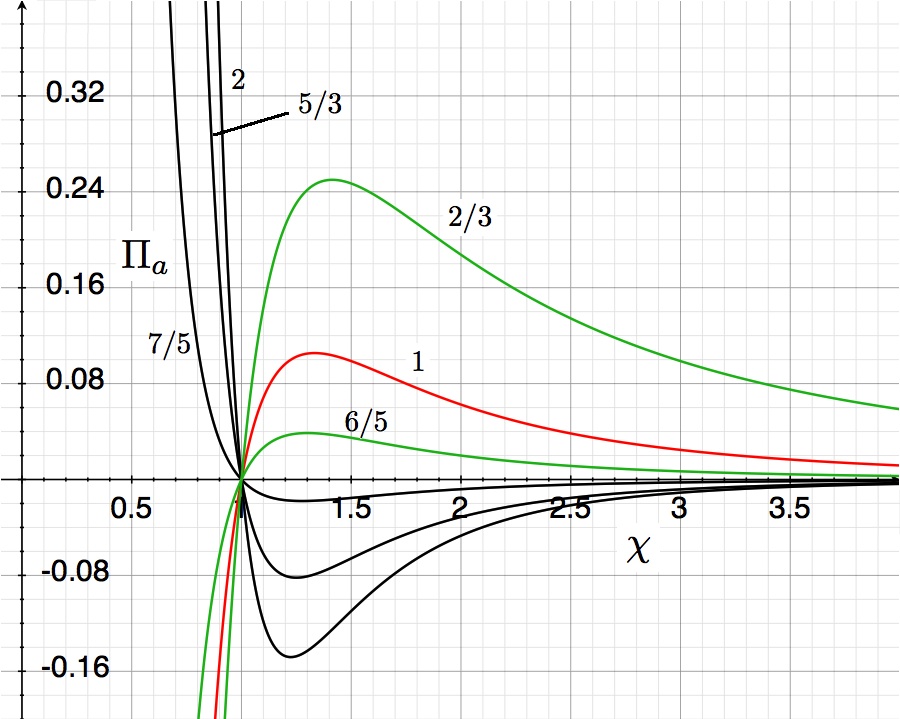
As has just been demonstrated, the virial theorem provides a mathematical expression that allows us to ''relate'' the equilibrium radius of a configuration to the applied external pressure, once the configuration's mass and either its specific entropy or central pressure are specified. In contrast to this, as has been [[User:Tohline/SSC/Structure/PolytropesEmbedded#Embedded_Polytropic_Spheres|discussed in detail in another chapter]], [http://adsabs.harvard.edu/abs/1970MNRAS.151...81H Horedt (1970)], [http://adsabs.harvard.edu/abs/1981MNRAS.195..967W Whitworth (1981)] and [http://adsabs.harvard.edu/abs/1983ApJ...268..165S Stahler (1983)] have each derived separate analytic expressions for <math>~R_\mathrm{eq}</math> and <math>~P_e</math> — given in terms of the Lane-Emden function, <math>~\Theta</math>, and its radial derivative — without demonstrating how the equilibrium radius and external pressure directly relate to one another. That is to say, solution of the detailed force-balanced equations provides a pair of equilibrium expressions that are parametrically related to one another through the Lane-Emden function. For example — see our [[User:Tohline/SSC/Structure/PolytropesEmbedded#Horedt.27s_Presentation|related discussion for more details]] — Horedt derives the following set of parametric equations relating the configuration's dimensionless radius, <math>~r_a</math>, to a specified dimensionless bounding pressure, <math>~p_a</math>: | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~r_a \equiv \frac{R_\mathrm{eq}}{R_\mathrm{Horedt}} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~p_a \equiv \frac{P_\mathrm{e}}{P_\mathrm{Horedt}} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~R_\mathrm{Horedt} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl[ \frac{4\pi}{(n+1)^n}\biggl( \frac{G}{K} \biggr)^n M_\mathrm{limit}^{n-1} \biggr]^{1/(n-3)} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~P_\mathrm{Horedt} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
K^{4n/(n-3)}\biggl[ \frac{(n+1)^3}{4\pi G^3 M_\mathrm{limit}^2} \biggr]^{(n+1)/(n-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
It is important to appreciate that, in the expressions for <math>~r_a</math> and <math>~p_a</math>, the tilde indicates that the Lane-Emden function and its derivative are to be evaluated, not at the radial coordinate, <math>~\xi_1</math>, that is traditionally associated with the "first zero" of the Lane-Emden function and therefore with the surface of the ''isolated polytrope,'' but at the radial coordinate, <math>~\tilde\xi</math>, where the internal pressure of the isolated polytrope equals <math>~P_e</math> and at which the ''embedded'' polytrope is to be truncated. The coordinate, <math>~\tilde\xi</math>, therefore identifies the surface of the embedded — or, pressure-truncated — polytrope. We also have taken the liberty of attaching the subscript "limit" to <math>~M</math> in both defining relations because it is clear that Hoerdt intended for the normalization mass to be the mass of the pressure-truncated object, not the mass of the associated ''isolated'' (and untruncated) polytrope. In anticipation of further derivations, below, we note here the ratio of Hoerdt's normalization parameters to ours, assuming <math>~\gamma = (n+1)/n</math>: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{R_\mathrm{Hoerdt}}{R_\mathrm{norm}} \biggr)^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{4\pi}{(n+1)^n}\biggl( \frac{G}{K} \biggr)^n M_\mathrm{limit}^{n-1} \biggr] | |||
\biggl[ \biggl( \frac{K}{G}\biggr)^n M_\mathrm{tot}^{1-n}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{P_\mathrm{Hoerdt}}{P_\mathrm{norm}} \biggr)^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
K^{4n}\biggl[ \frac{(n+1)^3}{4\pi G^3 M_\mathrm{limit}^2} \biggr]^{n+1} \biggl[ \frac{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}}{K^{4n}} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{n+1} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Next, we demonstrate that this pair of parametric relations satisfies the virial theorem and, in so doing, demonstrate how <math>~r_a</math> and <math>~p_a</math> may be ''directly'' related to each other. Given that Hoerdt's chosen normalization radius and normalization pressure are defined in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math>, we begin with the [[User:Tohline/SSC/Virial/Polytropes#Solution_Expressed_in_Terms_of_K_and_M_.28Whitworth.27s_1981_Relation.2|virial theorem derived above]] in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math>, setting <math>~\gamma_g = (n+1)/n</math>. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_e </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{(n+1)/n}} | |||
- \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
After setting <math>~R_\mathrm{eq} = r_a R_\mathrm{Horedt} </math>, a bit of algebraic manipulation shows that the first term on the right-hand side of the virial equilibrium expression becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{(n+1)/n}} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
r_a^{-3(n+1)/n} \mathfrak{f}_A \biggl[ \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{n-3} \frac{(n+1)^{3n}}{(4\pi)^n}\biggr]^{(n+1)/[n(n-3)]} | |||
[K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
while the second term on the right-hand side becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} (4\pi)^{-(n+1)/(n-3)} (n+1)^{4n/(n-3)}~ | |||
[K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
But, using Horedt's expression for <math>~P_e</math>, the left-hand side of the virial equilibrium equation becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_e = p_a P_\mathrm{Hoerdt}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
p_a~(4\pi)^{-(n+1)/(n-3)} ~(n+1)^{3(n+1)/(n-3)} | |||
[K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, the statement of virial equilibrium is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
p_a~ | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggr\{ r_a^{-3(n+1)/n} \mathfrak{f}_A \biggl[ \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{n-3} \frac{(n+1)^{3n}}{(4\pi)^n}\biggr]^{(n+1)/[n(n-3)]} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~~ | |||
- \frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} (4\pi)^{-(n+1)/(n-3)} (n+1)^{4n/(n-3)} \biggr\}(4\pi)^{(n+1)/(n-3)} ~(n+1)^{-3(n+1)/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M \cdot r_a^3} \biggr)^{(n+1)/n} | |||
- \frac{3(n+1)}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or, multiplying through by <math>~r_a^4</math> and rearranging terms, | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} r_a^{(n-3)/n} - p_a r_a^4 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3(n+1)}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
Now, Hoerdt has given analytic expressions for <math>~r_a</math> and <math>~p_a</math> in terms of the Lane-Emden function and its first derivative. The question is, what should the expressions for our structural form factors be in order for this virial expression to hold true for all pressure-truncated polytropic structures? As has been [[User:Tohline/SSC/Virial/Polytropes#Summary|summarized above]], in the case of an ''isolated'' polytrope, whose surface is located at <math>~\xi_1</math> and whose global properties are defined by evaluation of the Lane-Emden function at <math>~\xi_1</math>, we know that (see the [[User:Tohline/SSC/Virial/Polytropes#Summary|above summary]]), | |||
<div align="center"> | |||
<table border="0" align="center" cellpadding="5"> | |||
<tr><th align="center" colspan="1"> | |||
Structural Form Factors for <font color="red">Isolated</font> Polytropes | |||
</th></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{f}_M</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\xi_1} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\mathfrak{f}_W </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\xi_1} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\mathfrak{f}_A </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\xi_1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
These same expressions may or may not work for pressure-truncated polytropes, even if the evaluation radius is shifted from <math>~\xi_1</math> to <math>~\tilde\xi</math>. Let's see … | |||
<font color="red"><b> | |||
January 13, 2015: | |||
</b></font> | |||
As is noted in our [[User:Tohline/SSC/Virial/PolytropesEmbeddedOutline#Third_Effort|accompanying outline of work]], I no longer believe that <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_A</math> have the same expressions as in isolated polytropes. Hence, all of the material that follows is suspect and needs to be reworked. | |||
{{LSU_WorkInProgress}} | |||
Inserting Hoerdt's expressions for <math>~r_a</math> and <math>~p_a</math> into the viral equilibrium expression, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\frac{3(n+1)}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{(n-3)/n} | |||
~-~ | |||
\tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{4} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{(n-3)/n} | |||
~-~ | |||
\tilde\theta_n^{n+1} \tilde\xi^4 [( -\tilde\xi^2 \tilde\theta' )^{2(n+1)+4(1-n)} ]^{1/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi^{(n-3)} ( -\tilde\xi^2 \tilde\theta' )^{(1-n)} ]^{1/n} | |||
~-~ | |||
\tilde\theta_n^{n+1} \tilde\xi^4 [( -\tilde\xi^2 \tilde\theta' )^{-2} ] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} \tilde\xi^{-(n+1)/n} ( -\tilde\theta' )^{(1-n)/n} | |||
~-~ | |||
\frac{\tilde\theta_n^{n+1} }{( -\tilde\theta' )^{2} } \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
If we assume that both of the structural form factors, <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_M</math>, have the same functional expressions as in the case of isolated polytropes (but evaluated at <math>~\tilde\xi</math> instead of at <math>~\xi_1</math>), the virial relation further reduces to the form, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\frac{\tilde\theta_n^{n+1} }{( -\tilde\theta' )^{2} } | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{f}_A \biggl( \frac{\tilde\xi}{- \tilde\theta'} \biggr)^{(n+1)/n} \tilde\xi^{-(n+1)/n} ( -\tilde\theta' )^{(1-n)/n} - \frac{3(n+1)}{5-n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\mathfrak{f}_A}{(- \tilde\theta' )^2} - \frac{3(n+1)}{5-n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\Rightarrow~~~\mathfrak{f}_A | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3(n+1)}{5-n} (- \tilde\theta' )^2 + \tilde\theta_n^{n+1} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This all seems to make a great deal of sense. Only the structural parameter that is derived from an integral over the pressure distribution, <math>~\mathfrak{f}_A</math>, gets modified when the polytropic configuration is truncated. Notice, as well, that the term that has been added to the definition of <math>~\mathfrak{f}_A</math> naturally goes to zero in the limit of <math>~\tilde\xi \rightarrow \xi_1</math>, that is, for an isolated polytrope. We should definitely go back to the original definitions of all three structural parameters and prove that this is the case. But, in the meantime, here is the summary: | |||
<div align="center" id="PTtable"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr><th align="center" colspan="1"> | |||
<font size="+1" color="red"><b>WRONG!!</b></font> For the correct form-factor expressions, go [[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#Free-Energy_of_Truncated_Polytropes|here]]. | |||
</th></tr> | |||
<tr><th align="center" colspan="1"> | |||
Structural Form Factors for <font color="red">Pressure-Truncated</font> Polytropes | |||
</th></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tilde\mathfrak{f}_M</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\tilde\xi} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_W </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\tilde\xi} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_A </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\tilde\xi} + \tilde\Theta^{n+1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<font size="+1" color="red"><b>WRONG!!</b></font> For the correct form-factor expressions, go [[User:Tohline/SSC/FreeEnergy/PolytropesEmbedded#Free-Energy_of_Truncated_Polytropes|here]]. | |||
Notice that, in an effort to differentiate them from their counterparts developed earlier for "isolated" polytropes, we have affixed a tilde to each of these three form-factors, <math>~\mathfrak{f}_i</math>. | |||
====Example==== | |||
=====Outline===== | |||
Let's identify an equilibrium configuration numerically, using the free-energy expression. From [[User:Tohline/SphericallySymmetricConfigurations/Virial#Gathering_it_all_Together|our introductory discussion]], the relevant expression is, | |||
<div align="center"> | |||
<math> | |||
\mathfrak{G}^* = | |||
-3\mathcal{A} \chi^{-1} -~ \frac{1}{(1-\gamma_g)} \mathcal{B} \chi^{3-3\gamma_g} +~ \mathcal{D}\chi^3 \, , | |||
</math> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi}{3} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} | |||
\cdot \mathfrak{f}_A | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi}{3} | |||
\biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} | |||
\cdot \mathfrak{f}_A \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{D}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="1" cellpadding="10" align="center"> | |||
<tr><td align="left"> | |||
For later use, note that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{\mathcal{A}}{\mathcal{B}} \biggr)^n</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ | |||
\frac{3}{20\pi} \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]^{-(n+1)/n} | |||
\cdot \mathfrak{f}_A^{-1} | |||
\biggr\}^n</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~5^{-n} | |||
\biggl( \frac{3}{4\pi} \biggr)^n \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^{2n} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]^{-(n+1)} | |||
\cdot \biggl( \frac{\mathfrak{f}_W}{\mathfrak{f}_A} \biggr)^{n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{5^n} \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} | |||
\cdot \frac{\mathfrak{f}_W^n}{\mathfrak{f}_A^n \mathfrak{f}_M^{1-n}} \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\mathcal{B}^{4n}}{\mathcal{A}^{3(n+1)}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ | |||
\frac{1}{5} \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \biggr\}^{-3(n+1)} | |||
\biggl\{ \frac{4\pi}{3} | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]^{(n+1)/n} | |||
\cdot \mathfrak{f}_A | |||
\biggr\}^{4n}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
5^{3(n+1)} \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^{-6(n+1)} | |||
\biggl( \frac{4\pi}{3} \biggr)^{4n-4(n+1)} | |||
\biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]^{4(n+1)} \cdot\frac{\mathfrak{f}_A^{4n}}{\mathfrak{f}_W^{3(n+1)}} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
5^{3(n+1)} \biggl( \frac{3}{4\pi} \biggr)^{4} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2(n+1)} | |||
\cdot\frac{\mathfrak{f}_A^{4n} \mathfrak{f}_M^{2(n+1)} }{\mathfrak{f}_W^{3(n+1)}} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
</td></tr> | |||
</table> | |||
</div> | |||
Now, we could just blindly start setting values of the three leading coefficients, <math>~\mathcal{A}</math>, <math>~\mathcal{B}</math>, and <math>~\mathcal{D}</math>, then plot <math>~\mathfrak{G}^*(\chi)</math> to look for extrema. But let's accept a little guidance from this chapter's virial analysis before choosing the coefficient values. For embedded polytropes, we know that the structural form factors are, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tilde\mathfrak{f}_M = \frac{\bar\rho}{\rho_c}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\tilde\xi} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_W </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\tilde\xi} = \biggl( \frac{5}{5-n} \biggr) \tilde\mathfrak{f}_M^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_A = \frac{\bar{P}}{P_c}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{3(n+1) }{(5-n)} ~\biggl( \Theta^' \biggr)^2_{\tilde\xi} + \tilde\Theta^{n+1} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, the coefficient expressions become, | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>\frac{1}{(5-n)} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi}{3} | |||
\biggl( \frac{\bar{P}}{P_\mathrm{norm}} \biggr)\chi^{3(n+1)/n}_\mathrm{eq} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{D}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====Strategy===== | |||
Generic setup: | |||
* Choose the polytropic index, <math>~n</math>, which also sets the value of the adiabatic index, <math>~\gamma=(n+1)/n</math>. | |||
* Fix <math>~M_\mathrm{tot}</math> and <math>~K</math>, so that the radial and pressure normalizations are fixed; specifically, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{norm}^{n-3} = \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} </math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~P_\mathrm{norm}^{(n-3)} = K^{4n} (G^3 M_\mathrm{tot}^2)^{-(n+1)} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
* Fix <math>~M_\mathrm{limit}</math>, and let it be the normalization mass; that is, set <math>~M_\mathrm{limit} = M_\mathrm{tot}</math>. | |||
* As a result of the above choices, the value of <math>~\mathcal{A}</math> is set, and fixed; specifically, | |||
<div align="center"> | |||
<math>~A = \frac{1}{(5-n)} \, .</math> | |||
</div> | |||
'''<font color="red">Case I:</font>''' | |||
* Fix <math>~\mathcal{D}</math>, which fixes the external pressure; specifically, | |||
<div align="center"> | |||
<math>~P_e = \frac{3}{4\pi} \cdot \mathcal{D} P_\mathrm{norm} \, .</math> | |||
</div> | |||
* Choose a variety of values of the remaining coefficient, <math>~\mathcal{B}</math>; then, for each value, plot <math>\mathfrak{G}^*(\chi)</math> and locate one or more extrema along with the value of <math>~\chi_\mathrm{eq}</math> that is associated with each free energy extremum. This identifies the equilibrium value of the mean pressure inside the pressure-truncated polytrope via the expression, | |||
<div align="center"> | |||
<math>~ \bar{P} = \biggl(\frac{3}{4\pi} \biggr) P_\mathrm{norm}~\mathcal{B} ~\chi^{-3(n+1)/n}_\mathrm{eq} \, .</math> | |||
</div> | |||
* In order to check whether we've identified the correct value of <math>~\chi_\mathrm{eq}</math>, we have to relate it to the radial coordinate, <math>~\xi_e</math>, used in the analytic solution of the Lane-Emden equation. As has been explained in our [[User:Tohline/SSC/Structure/Polytropes#Polytropic_Spheres|discussion of detailed force-balanced models of polytropes]], generically, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{eq} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a_n \xi_e \, ,</math> where, | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~a_\mathrm{n} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr)\biggr]^{1/2} | |||
= | |||
\biggl[ \frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n}\biggr]^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl( \frac{a_n}{R_\mathrm{norm}} \biggr)^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{(n+1) K }{4\pi G} \biggr] \rho_c^{(1-n)/n} \cdot \frac{1}{R_\mathrm{norm}^2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{(n+1) K }{4\pi G} \biggr] \biggl( \frac{\rho_c}{\bar\rho} \biggr)^{(1-n)/n} | |||
\biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(1-n)/n} | |||
\cdot \frac{1}{R_\mathrm{norm}^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{(n+1) K }{4\pi G} \biggr] \biggl( \frac{\rho_c}{\bar\rho} \biggr)^{(1-n)/n} | |||
\biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr)^{(1-n)/n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{(1-n)/n} \chi_\mathrm{eq}^{3(n-1)/n} | |||
\cdot R_\mathrm{norm}^{(n-3)/n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(n+1) }{4\pi } | |||
\biggl[ \frac{3}{4\pi}\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(1-n)/n} | |||
\chi_\mathrm{eq}^{3(n-1)/n} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\xi_e^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{R_\mathrm{eq}}{a_n} \biggr)^2 = \chi_\mathrm{eq}^2 \biggl( \frac{a_n}{R_\mathrm{norm}} \biggr)^{-2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\chi_\mathrm{eq}^2 \biggl\{ | |||
\frac{4\pi }{(n+1) } | |||
\biggl[ \frac{3}{4\pi}\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n-1)/n} | |||
\chi_\mathrm{eq}^{3(1-n)/n} | |||
\biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4\pi }{(n+1) } | |||
\biggl[ \frac{3}{4\pi}\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n-1)/n} | |||
\chi_\mathrm{eq}^{(3-n)/n} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
But, from above, we also know that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{3}{4\pi}\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{3\mathcal{B}}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_A} \biggr]^{n/(n+1)} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_A = \frac{\bar{P}}{P_c}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{3(n+1) }{(5-n)} ~\biggl( \Theta^' \biggr)^2_{\tilde\xi} + \tilde\Theta^{n+1} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\xi_e^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4\pi }{(n+1) } | |||
\biggl[ \frac{3\mathcal{B}}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_A} \biggr]^{(n-1)/(n+1)} | |||
\chi_\mathrm{eq}^{(3-n)/n} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\xi_e^2 \biggl[ \frac{3(n+1) }{(5-n)} ~\biggl( \Theta^' \biggr)^2_{\tilde\xi} + \tilde\Theta^{n+1} \biggr]^{(n-1)/(n+1)}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4\pi }{(n+1) } | |||
\biggl[ \frac{3\mathcal{B}}{4\pi} \biggr]^{(n-1)/(n+1)} | |||
\chi_\mathrm{eq}^{(3-n)/n} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This last expression may be useful because the numerical value of the right-hand-side will be known once an extremum of a free-energy plot has been identified, while the function on the left-hand side can be evaluated separately, from knowledge of the internal structure of detailed force-balanced, ''isolated'' polytropes. | |||
=====Strategy2===== | |||
* Pick the desired polytropic index, <math>~n</math>, and a radial coordinate within the isolated polytropic model, <math>~\tilde\xi \leq \xi_1</math>, that will serve as the truncated edge of the embedded polytrope. | |||
* Knowledge of the isolated polytrope's internal structure will give the value of the Lane-Emden function, <math>~\tilde\theta</math>, and its radial derivative, <math>~{\tilde\theta'}</math>, at this truncated edge of the structure. | |||
* According to [http://adsabs.harvard.edu/abs/1970MNRAS.151...81H Horedt (1970)] — see our [[User:Tohline/SSC/Structure/PolytropesEmbedded#Horedt.27s_Presentation|accompanying discussion of detailed force-balanced models]] — the physical radius and external pressure that corresponds to this choice of the truncated edge is given by the expressions, | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} = r_a \biggl( \frac{R_\mathrm{Horedt}}{R_\mathrm{norm}} \biggr) | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \biggl[ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{n-1} \biggr]^{1/(n-3)} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~\frac{P_e}{P_\mathrm{norm}} = p_a \biggl( \frac{P_\mathrm{Horedt}}{P_\mathrm{norm}} \biggr) | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2} \biggr]^{(n+1)/(n-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
* Using the chosen value of <math>~\tilde\xi</math> and its associated function values, <math>~\tilde\theta</math> and <math>~\tilde\theta^'</math>, determine the values of the three relevant structural form factors via the following analytic relations: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tilde\mathfrak{f}_M = \frac{\bar\rho}{\rho_c}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ - \frac{3 \tilde\theta^'}{\tilde\xi} \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_W </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\tilde\theta^'}{\tilde\xi} \biggr]^2 = \biggl( \frac{5}{5-n} \biggr) \tilde\mathfrak{f}_M^2 \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_A = \frac{\bar{P}}{P_c}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{3(n+1) }{(5-n)} ~( \tilde\theta^')^2 + \tilde\theta^{n+1} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
* Using these values of the structural form factors, determine the values of the three free-energy coefficients (set <math>~M_\mathrm{limi}/M_\mathrm{tot} = 1</math> for the time being) via the expressions: | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}_\mathrm{mod} \equiv (5-n)\mathcal{A}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>\frac{(5-n)}{5} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} | |||
= \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B}_\mathrm{mod} \equiv (5-n)\mathcal{B}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{3}{4\pi} \biggr)^{1/n} | |||
\biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{(n+1)/n} | |||
\cdot [(5-n)\tilde\mathfrak{f}_A] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi}{3} \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^{3(n+1)/n} | |||
\cdot [(5-n)\tilde\mathfrak{f}_A] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{D}_\mathrm{mod} \equiv (5-n) \mathcal{D}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{4\pi}{3} \biggr) (5-n) \frac{P_e}{P_\mathrm{norm}} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
* Plot the following free-energy function and see if the value of <math>~\chi</math> associated with the extremum is equal to the dimensionless equilibrium radius, <math>~R_\mathrm{eq}/R_\mathrm{norm}</math>, as predicted by Hoerdt's expression, above: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(5-n)\mathfrak{G}^*</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-3\mathcal{A}_\mathrm{mod} \chi^{-1} -~ \frac{1}{(1-\gamma_g)} \mathcal{B}_\mathrm{mod} \chi^{3-3\gamma_g} +~ \mathcal{D}_\mathrm{mod}\chi^3</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-3\mathcal{A}_\mathrm{mod} \chi^{-1} +n\mathcal{B}_\mathrm{mod} \chi^{-3/n} +~ \mathcal{D}_\mathrm{mod}\chi^3 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
* Virial equilbrium — that is, an extremum in the free energy function — occurs when <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>, that is, where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B}_\mathrm{mod} \chi_\mathrm{eq}^{(n-3)/n} - \mathcal{D}_\mathrm{mod}\chi_\mathrm{eq}^4</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathcal{A}_\mathrm{mod} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Note that if the coefficient, <math>~\mathcal{B}</math>, is written in terms of the normalized central pressure, the statement of virial equilibrium becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}_\mathrm{mod} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{4\pi}{3}\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^{3(n+1)/n} | |||
\cdot [(5-n)\tilde\mathfrak{f}_A] \biggr] \chi_\mathrm{eq}^{(n-3)/n} - \frac{4\pi}{3} (5-n)\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^4</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4\pi}{3}\chi_\mathrm{eq}^4 \biggl\{\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) | |||
\cdot (5-n)\tilde\mathfrak{f}_A - (5-n)\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4\pi}{3}\chi_\mathrm{eq}^4 \biggl\{\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) | |||
\cdot \biggl[ 3(n+1) (\tilde\theta^')^2 + (5-n)\tilde\theta^{n+1} \biggr] - (5-n)\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
But, in this situation, <math>~\tilde\theta^{n+1} = P_e/P_c</math>, so virial equilibrium implies, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{3}{4\pi}\chi_\mathrm{eq}^{-4} \mathcal{A}_\mathrm{mod} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) | |||
\cdot \biggl[ 3(n+1) (\tilde\theta^')^2 + (5-n)\frac{P_e}{P_c} \biggr] - (5-n)\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3(n+1) (\tilde\theta^')^2\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\frac{P_c}{P_\mathrm{norm}} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ 4\pi(n+1) (\tilde\theta^')^2 \biggr]^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\frac{P_c R_\mathrm{eq}^4}{GM_\mathrm{limit}^2} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{4\pi(n+1) (\tilde\theta^')^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====Compare With Detailed Force Balanced Solution===== | |||
In a [[User:Tohline/SSC/Structure/PolytropesEmbedded#.3D_1_Polytrope|separate discussion]], we presented the detailed force-balanced model of an <math>~n=1</math> polytrope that is embedded in an external medium. We showed that, for an applied external pressure given by, | |||
<div align="center"> | |||
<math>\frac{P_e}{P_\mathrm{norm}} = \frac{\pi}{2} \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2 \, ,</math> | |||
</div> | |||
the associated equilibrium radius of the pressure-confined configuration is, | |||
<div align="center"> | |||
<math> | |||
R_\mathrm{eq} = \xi_e a_\mathrm{n=1} = \biggl[ \frac{K}{2\pi G} \biggr]^{1/2} \xi_e \, . | |||
</math> | |||
</div> | |||
Flipping this around, after we use a plot of the free-energy expression to identify the equilibrium radius, <math>~\chi_\mathrm{eq}</math>, the corresponding dimensionless radius as used in the Lane-Emden equation should be, | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\xi_e</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl[ \frac{2\pi G}{K} \biggr]^{1/2} R_\mathrm{norm} \cdot \chi_\mathrm{eq} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(2\pi)^{1/2} \chi_\mathrm{eq} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Keep in mind that, for an [[User:Tohline/SSC/Structure/Polytropes#.3D_1_Polytrope|isolated <math>~n=1</math> polytrope]], the (zero pressure) surface is identified by <math>~\xi_1 = \pi</math>. Hence we should expect free-energy extrema to occur at values of <math>~\chi_\mathrm{eq} \le \pi/2</math>. | |||
====Renormalization==== | |||
=====Grunt Work===== | |||
Returning to the dimensionless form of the virial expression and multiplying through by <math>~[-\chi_\mathrm{eq}/(3D)]</math>, we obtain, | |||
<div align="center"> | |||
<math> | |||
\chi_\mathrm{eq}^4 = \frac{B}{D} \chi_\mathrm{eq}^{4-3\gamma_g} - \frac{A}{D} \, , | |||
</math> | |||
</div> | |||
or, after plugging in [[User:Tohline/SphericallySymmetricConfigurations/Virial#Gathering_it_all_Together|definitions of the coefficients]], <math>~A</math>, <math>~B</math>, and <math>~D</math>, and rewriting <math>~\chi_\mathrm{eq}</math> explicitly as <math>~R_\mathrm{eq}/R_\mathrm{norm}</math>, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} | |||
\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}} | |||
\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{4-3\gamma_g} - | |||
\frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} | |||
\frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This relation can be written in a more physically concise form, as follows. First, normalize <math>~P_e</math> to a new pressure scale — call it <math>~P_\mathrm{ad}</math> — and multiply through by <math>~(R_\mathrm{norm}/R_\mathrm{ad})^4</math> in order to normalizing <math>~R_\mathrm{eq}</math> to a new length scale,<math>~R_\mathrm{ad}</math>: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{ad}} \biggr)^4 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} | |||
\biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{P_e}{P_\mathrm{ad}} \biggr)^{-1} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}} | |||
\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g}\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{ad}} \biggr)^{4-3\gamma_g} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math> | |||
~- | |||
\frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) | |||
\frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggl( \frac{P_e}{P_\mathrm{ad}} \biggr)^{-1} \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad}^4 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} | |||
\biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g} | |||
\frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}}\cdot \frac{\chi_\mathrm{ad}^{4-3\gamma_g} }{\Pi_\mathrm{ad}} - | |||
\frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} | |||
\biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} | |||
\frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \cdot \frac{1}{\Pi_\mathrm{ad}} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{ad}} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{P_\mathrm{e}}{P_\mathrm{ad}} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
By demanding that the leading coefficients of both terms on the right-hand-side of the expression are simultaneously unity — that is, by demanding that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} | |||
\biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g} | |||
\frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} | |||
\biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} | |||
\frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we obtain the expressions for <math>~R_\mathrm{ad}/R_\mathrm{norm}</math> and <math>~P_\mathrm{ad}/P_\mathrm{norm}</math> as shown in the following table. | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr><th align="center" colspan="1"> | |||
Renormalization for Adiabatic (''ad'') Systems | |||
</th></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{R_\mathrm{ad}}{R_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{1}{5} \biggl( \frac{4\pi}{3} \biggr)^{\gamma_g-1} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2-\gamma_g} | |||
\frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_A \cdot \tilde\mathfrak{f}_M^{2-\gamma_g}} \biggr]^{1/(4-3\gamma_g)} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ | |||
\frac{1}{5^n} \biggl( \frac{4\pi}{3}\biggr)\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{n-1} | |||
\frac{\tilde\mathfrak{f}_W^n}{\tilde\mathfrak{f}_A^n \cdot \tilde\mathfrak{f}_M^{n-1}} | |||
\biggr]^{1/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{P_\mathrm{ad}}{P_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ \tilde\mathfrak{f}_A^4 \cdot \biggl( \frac{3\cdot 5^3}{4\pi} \cdot | |||
\frac{\tilde\mathfrak{f}_M^2}{\tilde\mathfrak{f}_W^3} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2\gamma_g} \biggr]^{1/(4-3\gamma)} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ | |||
\tilde\mathfrak{f}_A^{4n} \biggl(\frac{3\cdot 5^3}{4\pi} \biggr)^{n+1} \biggl( \frac{\tilde\mathfrak{f}_M^2}{\tilde\mathfrak{f}_w^3} \biggr)^{n+1} | |||
\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2(n+1)} | |||
\biggr]^{1/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Using these new normalizations, we arrive at the desired, concise virial equilibrium relation, namely, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\chi_\mathrm{ad}^{-3\gamma_g} - \chi_\mathrm{ad}^{-4} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad}^{4-3\gamma_g} - \Pi_\mathrm{ad} \chi_\mathrm{ad}^4</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
For the sake of completeness, we should develop expressions for both <math>~\chi_\mathrm{ad}</math> and <math>~\Pi_\mathrm{ad}</math> that are entirely in terms of the Lane-Emden function, <math>~\tilde\theta</math>, its derivative, <math>~\tilde\theta'</math>, and the associated dimensionless radial coordinate, <math>\tilde\xi</math>, at which the function and its derivative are to be evaluated. (Adopting a unified notation, we will set <math>~\gamma_g \rightarrow (n+1)/n</math>.) | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{ad}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{Hoerdt}} \cdot \frac{R_\mathrm{Hoerdt}}{R_\mathrm{norm}} \cdot \frac{R_\mathrm{norm}}{R_\mathrm{ad}}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
r_a \cdot \biggl[ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} \biggr]^{1/(n-3)} \cdot | |||
\biggl[ 5^n \biggl( \frac{3}{4\pi} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{1-n} | |||
\frac{\tilde\mathfrak{f}_A^n}{\tilde\mathfrak{f}_W^n \cdot \tilde\mathfrak{f}_M^{1-n}} | |||
\biggr]^{1/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\chi_\mathrm{ad}^{n-3} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
3 r_a^{n-3} \cdot \biggl[ \frac{5}{(n+1)} \cdot | |||
\frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_W} \biggr]^n \tilde\mathfrak{f}_M^{n-1} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Inserting the functional expressions for Hoerdt's <math>~r_a</math> and our structural form factors, <math>\tilde\mathfrak{f}_i</math>, gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad}^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
3 \tilde\mathfrak{f}_A^n \biggl[ \tilde\xi^{n-3} (-\tilde\xi^2 \tilde\theta')^{1-n} \biggr] | |||
\biggl[ \frac{5}{(n+1)} \cdot \frac{(5-n)}{5\cdot 3^2} \biggl( - \frac{\tilde\xi}{\tilde\theta'} \biggr)^2\biggr]^n \biggl[- \frac{3 \tilde\theta'}{\tilde\xi} \biggr]^{n-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{(5-n)}{3(n+1)} \cdot \frac{\tilde\mathfrak{f}_A}{(-\tilde\theta')^2}\biggr]^n | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~~ \chi_\mathrm{ad}^{(n-3)/n}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{(5-n)}{3(n+1)} \cdot (-\tilde\theta')^{-2} \biggl[ \frac{3(n+1)}{(5-n)} (-\tilde\theta')^2 + \theta^{n+1} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 + | |||
\frac{(5-n)}{3(n+1)} \cdot \frac{\tilde\theta^{n+1}}{(-\tilde\theta')^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
And, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad} \equiv \frac{P_e}{P_\mathrm{ad}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{P_e}{P_\mathrm{Hoerdt}} \cdot \frac{P_\mathrm{Hoerdt}}{P_\mathrm{norm}} \cdot \frac{P_\mathrm{norm}}{P_\mathrm{ad}}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
p_a \cdot \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{(n+1)/(n-3)} \cdot | |||
\biggl[ \tilde\mathfrak{f}_A^{-4n} \cdot \biggl( \frac{4\pi}{3\cdot 5^3} \cdot | |||
\frac{\tilde\mathfrak{f}_W^3}{\tilde\mathfrak{f}_M^2} \biggr)^{(n+1)} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2(n+1)} | |||
\biggr]^{1/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\Pi_\mathrm{ad}^{n-3} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
p_a^{n-3}~ \tilde\mathfrak{f}_A^{-4n} \cdot \biggl[ | |||
\frac{(n+1)^3}{3\cdot 5^3} \biggl( \frac{\tilde\mathfrak{f}_W^3}{\tilde\mathfrak{f}_M^2} \biggr) | |||
\biggr]^{n+1} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Inserting the functional expressions for Hoerdt's <math>~p_a</math> and our structural form factors, <math>\tilde\mathfrak{f}_i</math>, gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad}^{n-3} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\tilde\mathfrak{f}_A^{-4n} ~[ \tilde\theta^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} ]^{n-3} \cdot \biggl[ | |||
\frac{(n+1)^3}{3\cdot 5^3}\biggr]^{n+1} | |||
\biggl[ \frac{3^2\cdot 5}{5-n} \biggl( \frac{\tilde\theta^'}{\tilde\xi} \biggr)^2 \biggr]^{3(n+1)} | |||
\bigg( - \frac{3\tilde\theta^'}{\tilde\xi} \biggr)^{-2(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\tilde\mathfrak{f}_A^{-4n} ~\biggl\{ | |||
\tilde\theta^{n-3}( -\tilde\xi^2 \tilde\theta' )^{2} \cdot \biggl[ | |||
\frac{(n+1)^3}{3\cdot 5^3}\biggr] | |||
\biggl[ \frac{3^2\cdot 5}{5-n} \biggl( \frac{\tilde\theta^'}{\tilde\xi} \biggr)^2 \biggr]^{3} | |||
\bigg( - \frac{3\tilde\theta^'}{\tilde\xi} \biggr)^{-2} | |||
\biggr\}^{n+1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\tilde\theta^{(n+1)(n-3)} | |||
\tilde\mathfrak{f}_A^{-4n} ~\biggl[ \frac{3(n+1)}{(5-n)} ( -\tilde\theta' )^{2} \biggr]^{3(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\tilde\theta^{(n+1)(n-3)} | |||
\biggl[ \frac{3(n+1) }{(5-n)} ~( \tilde\theta^' )^2 + \tilde\theta^{n+1} \biggr]^{-4n} | |||
~\biggl[ \frac{3(n+1)}{(5-n)} ( \tilde\theta' )^{2} \biggr]^{3(n+1)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
(Not a particularly simple or transparent expression!) | |||
=====Summary===== | |||
Defining, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a_\mathrm{ad}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3(n+1) }{(5-n)} ~(\tilde\theta^' )^2 \, ,</math> and, | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~b_\mathrm{ad}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\tilde\theta^{n+1} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
the expressions for the dimensionless equilibrium radius and the dimensionless external pressure may be written as, respectively, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1 + \frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggr]^{n/(n-3)} \, , | |||
</math> and, | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
b_\mathrm{ad} \biggl[ \frac{a_\mathrm{ad}^{3(n+1)} }{( a_\mathrm{ad} + b_\mathrm{ad} )^{4n} } \biggr]^{1/(n-3)} | |||
= | |||
\frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggl[ 1 + \frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggr]^{-4n/(n-3)} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Using these expressions, it is easy to demonstrate that the virial equilibrium relation is satisfied, namely, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\chi_\mathrm{ad}^{-3(n+1)/n} - \chi_\mathrm{ad}^{-4} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
{{LSU_WorkInProgress}} | |||
====P-V Diagram for Unity Form Factors==== | |||
Writing the coefficient, <math>B</math>, in terms of the average sound speed and setting the radial scale factor equal to the equilibrium radius of an isolated adiabatic sphere, that is, setting, | |||
<div align="center"> | |||
<math> | |||
R_0 = \frac{GM}{5\bar{c_s}^2} \, , | |||
</math> | |||
</div> | |||
the equation governing the radii of ''adiabatic'' equilibrium states becomes, | |||
<div align="center"> | |||
<math> | |||
\chi^4 - \frac{1}{\Pi_a} \chi^{(4-3\gamma_g)} + \frac{1}{\Pi_a} = 0 \, , | |||
</math> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<math> | |||
\Pi_a \equiv \frac{4\pi P_e G^3 M^2}{3\cdot 5^3 \bar{c_s}^8} \, . | |||
</math> | |||
</div> | |||
As in the isothermal case, for a given choice of configuration mass and sound speed, this parameter, <math>\Pi_a</math>, can be viewed as a dimensionless external pressure. Alternatively, for a given choice of <math>P_e</math> and <math>\bar{c_s}</math>, <math>\Pi_a^{1/2}</math> can represent a dimensionless mass; or, for a given choice of <math>M</math> and <math>P_e</math>, <math>\Pi_a^{-1/8}</math> can represent a dimensionless sound speed. Here we will view it as a dimensionless external pressure. | |||
Unlike the isothermal case, for an arbitrary value of the adiabatic exponent, <math>\gamma_g</math>, it isn't possible to invert this equation to obtain an analytic expression for <math>\chi</math> as a function of <math>\Pi_a</math>. But we can straightforwardly solve for <math>\Pi_a</math> as a function of <math>\chi</math>. The solution is, | |||
<div align="center"> | |||
<math> | |||
\Pi_a = \frac{\chi^{(4- 3\gamma_g)} - 1}{\chi^4} \, . | |||
</math> | |||
</div> | |||
For physically relevant solutions, both <math>\chi</math> and <math>\Pi_a</math> must be nonnegative. Hence, as is illustrated by the curves in Figure 4, the physically allowable range of equilibrium radii is, | |||
<div align="center"> | |||
<math> | |||
1 \le \chi \le \infty \, ~~~~~\mathrm{for}~ \gamma_g < 4/3 \, ; | |||
</math> | |||
<math> | |||
0 < \chi \le 1 \, ~~~~~~\mathrm{for}~ \gamma_g > 4/3 \, . | |||
</math> | |||
</div> | |||
<div align="center"> | |||
<table border="2" cellpadding="8"> | |||
<tr> | |||
<td align="center" colspan="2"> | |||
'''Figure 4:''' <font color="darkblue">Equilibrium Adiabatic P-V Diagram </font> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td valign="top" width=450 rowspan="1"> | |||
The curves trace out the function, | |||
<div align="center"> | |||
<math> | |||
\Pi_a = (\chi^{4-3\gamma_g} - 1)/\chi^4 \, , | |||
</math> | |||
</div> | |||
for six different values of <math>\gamma_g</math> (<math>2, ~5/3, ~7/5, ~6/5, ~1, ~2/3</math>, as labeled) and show the dimensionless external pressure, <math>\Pi_a</math>, that is required to construct a nonrotating, self-gravitating, uniform density, adiabatic sphere with an equilibrium radius <math>\chi</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative. | |||
The solid red curve, drawn for the case <math>\gamma_g = 1</math>, is identical to the solid black (isothermal) curve displayed above in Figure 1. | |||
</td> | |||
<td align="center" bgcolor="white"> | |||
[[File:AdabaticBoundedSpheres_Virial.jpg|450px|center|Equilibrium Adiabatic P-R Diagram]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Each of the <math>\Pi_a(\chi)</math> curves drawn in Figure 4 exhibits an extremum. In each case this extremum occurs at a configuration radius, <math>\chi_\mathrm{extreme}</math>, given by, | |||
<div align="center"> | |||
<math> | |||
\frac{\partial\Pi_a}{\partial\chi} = 0 \, , | |||
</math> | |||
</div> | |||
that is, where, | |||
<div align="center"> | |||
<math> | |||
4 - 3\gamma_g \chi^{4-3\gamma_g} = 0 ~~~~\Rightarrow ~~~~~ \chi_\mathrm{extreme} = \biggl[ \frac{4}{3\gamma_g} \biggr]^{1/(4-3\gamma_g)} \, . | |||
</math> | |||
</div> | |||
For each value of <math>\gamma_g</math>, the corresponding dimensionless pressure is, | |||
<div align="center"> | |||
<math> | |||
\Pi_a \biggr|_\mathrm{extreme} = \biggl(\frac{4}{3\gamma} - 1 \biggr) \biggl[ \frac{3\gamma_g}{4} \biggr]^{4/(4-3\gamma_g)} \, . | |||
</math> | |||
</div> | |||
Note, first, that for <math>\gamma_g > 4/3</math>, an equilibrium configuration with a positive radius can be constructed for all physically realistic — that is, for all positive — values of <math>\Pi_a</math>. Also, consistent with the behavior of the curves shown in Figure 4, the extremum arises in the regime of physically relevant — ''i.e.,'' positive — pressures only for values of <math>\gamma_g < 4/3</math>; and in each case it represents a ''maximum'' limiting pressure. | |||
====Maximum Mass==== | |||
=====<math>n=5</math> Polytropic===== | |||
When <math>\gamma_a = 6/5</math> — which corresponds to an <math>n=5</math> polytropic configuration — we obtain, | |||
<div align="center"> | |||
<math> | |||
\Pi_\mathrm{max} = \Pi_a\biggr|_\mathrm{extreme}^{(\gamma_g = 6/5)} | |||
= \biggl( \frac{3^{18}}{2^{10}\cdot 5^{10}} \biggr) \, , | |||
</math> | |||
</div> | |||
which corresponds to a maximum mass for pressure-bounded <math>n=5</math> polytropic configurations of, | |||
<div align="center"> | |||
<math>M_\mathrm{max} = \Pi_\mathrm{max}^{1/2} \biggl(\frac{3\cdot 5^3}{2^2\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} | |||
= \biggl(\frac{3^{19}}{2^{12}\cdot 5^{7}\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} \, .</math> | |||
</div> | |||
This result can be compared to [[User:Tohline/SSC/Structure/LimitingMasses#Bounded_Isothermal_Sphere_.26_Bonnor-Ebert_Mass|other determinations of the Bonnor-Ebert mass limit]]. | |||
====More Precise Form Factors==== | |||
Here we attempt to determine proper expressions for several form factors such that the equilibrium configurations determined from virial analysis will precisely match the [[User:Tohline/SSC/Structure/PolytropesEmbedded#Embedded_Polytropic_Spheres|pressure-truncated polytropic configurations]] that have been determined from detailed force-balanced models that have been derived and published separately by [http://adsabs.harvard.edu/abs/1970MNRAS.151...81H Horedt (1970)], by [http://adsabs.harvard.edu/abs/1981MNRAS.195..967W Whitworth (1981)] and by [http://adsabs.harvard.edu/abs/1983ApJ...268..165S Stahler (1983)]. It seems simplest to begin with the [[User:Tohline/SSC/BipolytropeGeneralization_Version2#Generalized_Free-Energy_Expression|free-energy expressions that we have already generalized in the context of bipolytropic configurations]], properly modified to embed the "core" in an external medium of pressure, <math>~P_e</math>, rather then inside an envelope that has a different polytropic index. Specifically, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}^* \equiv \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr)_\mathrm{core} | |||
+ \biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core} | |||
+ \biggl( \frac{P_e V}{E_\mathrm{norm}} \biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-3\mathcal{A} \chi^{-1} - \frac{\mathcal{B}_\mathrm{core}}{(1-\gamma_c)} \chi^{3-3\gamma_c} + \mathcal{D} \chi^3 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{\nu}{q^3} \biggr) \int_0^{q} \biggl[\frac{M_r(x)}{M_\mathrm{tot}} \biggr]_\mathrm{core} \biggl[ \frac{\rho(x)}{\bar\rho} \biggr]_\mathrm{core} x dx \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B}_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi}{3} \biggl[ \frac{P_{ic} \chi^{3\gamma_c}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \int_0^q 3\biggl[\frac{1 - p_c(x)}{1-p_c(q)} \biggr] x^2 dx | |||
= | |||
\frac{4\pi}{3} \biggl[ \frac{P_e \chi^{3\gamma_c}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \biggl[ q^3 s_\mathrm{core} \biggr] | |||
\, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{D}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\chi^{-3} \biggl[ \frac{P_e V}{P_\mathrm{norm} R_\mathrm{norm}^3} \biggr] = \biggl(\frac{P_e}{P_\mathrm{norm}} \biggr) \int_0^q 4\pi x^2 dx | |||
= \frac{4\pi q^3}{3} \biggl(\frac{P_e}{P_\mathrm{norm}} \biggr) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Virial equilibrium occurs where <math>~\partial\mathfrak{G}/\partial \chi = 0</math>, that is, when, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A} \chi_\mathrm{eq}^{-1}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathcal{B} \chi_\mathrm{eq}^{3-3\gamma_c} - \mathcal{D} \chi_\mathrm{eq}^{3} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====n = 5 Polytropic===== | |||
From our [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy5_1#Free_Energy_of_BiPolytrope_with|analysis of the free energy of <math>~(n_c, n_e) = (5, 0)</math> bipolytropes]], we deduce that the coefficient, <math>~\mathcal{A}</math>, that quantifies the [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy5_1#The_Core_2|gravitational potential energy of a pressure-truncated <math>~n = 5</math> polytrope]] is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A} = - \frac{\chi}{3} \biggl( \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr)_\mathrm{core} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\chi_\mathrm{eq} \biggl( \frac{3^6}{2^5\pi} \biggr)^{1/2} | |||
\biggl[ | |||
a_\xi^{1/2} q(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) (a_\xi q^2 +1)^{-3} + \tan^{-1}(a_\xi^{1/2} q) | |||
\biggr] \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
the coefficient, <math>~\mathcal{B}_\mathrm{core}</math>, that quantifies the [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy5_1#The_Core_3|thermal energy content of a pressure-truncated <math>~n = 5</math> polytrope]] is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B} = (\gamma_c-1) \chi^{3\gamma_c-3}\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\chi_\mathrm{eq}^{3/5} | |||
\biggl( \frac{3^6}{2^5\pi} \biggr)^{1/2} \biggl[ | |||
\tan^{-1}[a_\xi^{1/2}q] - a_\xi^{1/2}q ~\frac{(1 - a_\xi q^2)}{(1 + a_\xi q^2)^2} \biggr] \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and the coefficient, <math>~\mathcal{D}</math> — which can be obtained by setting <math>~P_{ic} \rightarrow P_e</math> in expressions drawn from out analysis of the [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy5_1#The_Core_3|thermal energy content of an <math>~(5, 0)</math>bipolytrope]] — is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>\mathcal{D} = \biggl(\frac{2q^3}{3 \chi_\mathrm{eq}^3} \biggr) \biggl[ \frac{2\pi P_{ic} \chi_\mathrm{eq}^3}{P_\mathrm{norm}} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\chi_\mathrm{eq}^{-3} \biggl( \frac{2\cdot 3^4}{\pi} \biggr)^{1/2} \biggl(1 + a_\xi q^2 \biggr)^{-3} a_\xi^{3/2}q^3 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, virial equilibrium occurs when, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A} \chi_\mathrm{eq}^{-1}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathcal{B} \chi_\mathrm{eq}^{-3/5} - \mathcal{D} \chi_\mathrm{eq}^{3} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
that is, when, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\biggl( \frac{3^6}{2^5\pi} \biggr)^{1/2} | |||
\biggl[ a_\xi^{1/2} q(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) (a_\xi q^2 +1)^{-3} + \tan^{-1}(a_\xi^{1/2} q)\biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{3^6}{2^5\pi} \biggr)^{1/2} \biggl[ | |||
\tan^{-1}[a_\xi^{1/2}q] - a_\xi^{1/2}q ~\frac{(1 - a_\xi q^2)}{(1 + a_\xi q^2)^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- | |||
\biggl( \frac{2\cdot 3^4}{\pi} \biggr)^{1/2} \biggl(1 + a_\xi q^2 \biggr)^{-3} a_\xi^{3/2}q^3 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~~ | |||
\biggl[ a_\xi^{1/2} q(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) (a_\xi q^2 +1)^{-3} + \tan^{-1}(a_\xi^{1/2} q)\biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \tan^{-1}[a_\xi^{1/2}q] - a_\xi^{1/2}q ~\frac{(1 - a_\xi q^2)}{(1 + a_\xi q^2)^2} \biggr] | |||
- | |||
\biggl( \frac{2^3}{3} \biggr) \biggl(1 + a_\xi q^2 \biggr)^{-3} a_\xi^{3/2}q^3</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~~ | |||
a_\xi^{1/2} q(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- a_\xi^{1/2}q ~(1 - a_\xi q^2)(1 + a_\xi q^2) | |||
- | |||
\biggl( \frac{2^3}{3} \biggr) a_\xi^{3/2}q^3</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~~ | |||
(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- (1 - a_\xi^2 q^4) - \biggl( \frac{2^3}{3} \biggr) a_\xi q^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~~ | |||
0 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
0 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So this will always be true! | |||
The [[User:Tohline/SSC/Structure/PolytropesEmbedded#Extension_to_Bounded_Sphere_2|detailed force-balanced analysis]] of <math>~n=5</math> polytropes shows that the pair of equations defining the equilibrium (truncated) radius for a specified external pressure are, | |||
<div align="center"> | |||
<math> | |||
R_\mathrm{eq} = \biggl[ \frac{\pi M^4 G^5}{2^3 \cdot 3^7 K^5} \biggr]^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \, , | |||
</math> | |||
<math>P_e= \biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 M^{6} G^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} </math> . | |||
</div> | |||
Applying our chosen normalizations, this pair of defining equations becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq} = \frac{R_\mathrm{eq}}{R_\mathrm{norm}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{\pi M^4 G^5}{2^3 \cdot 3^7 K^5} \biggr]^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} | |||
\cdot \biggl[\frac{K^5}{G^5 M_\mathrm{tot}^4} \biggr]^{1/2} | |||
= \biggl( \frac{\pi}{2^3 \cdot 3} \biggr)^{1/2} \xi_e^{-5} \biggl( 1+ \frac{1}{3}\xi_e^2 \biggr)^3 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{P_e}{P_\mathrm{norm}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 M^{6} G^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} | |||
\cdot \biggl[\frac{G^9 M_\mathrm{tot}^6}{K^{10}} \biggr] | |||
= \biggr( \frac{2^3\cdot 3^{3} }{\pi^3} \biggr) \xi_e^{18} \biggl(1 + \frac{1}{3}\xi_e^2 \biggr)^{-12} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Relationship to Detailed Force Balance Solution== | |||
Let's plug these form-factors into our expressions for the dimensionless equilibrium radius, <math>~\chi_\mathrm{ad}</math>, and dimensionless surface pressure, <math>~\Pi_\mathrm{ad}</math>, that have been derived from the identification of extrema in the free-energy function and see how they compare to the dimensionless radius, <math>~r_a \equiv R_\mathrm{eq}/R_\mathrm{Hoerdt}</math>, and dimensionless pressure, <math>~p_a \equiv P_e/P_\mathrm{Hoerdt}</math>, given by [http://adsabs.harvard.edu/abs/1970MNRAS.151...81H Horedt's (1970)] detailed force-balance models. Note that expressions for <math>~r_a</math> and <math>~p_a</math> are given in our [[User:Tohline/SSC/Structure/PolytropesEmbedded#Horedt.27s_Presentation|accompanying discussion of embedded polytropic spheres]] and that the conversion from Hoerdt's scaling parameters to our normalization parameters, <math>~R_\mathrm{Hoerdt}/R_\mathrm{norm}</math> and <math>~P_\mathrm{Hoerdt}/P_\mathrm{norm}</math>, can be found in our [[User:Tohline/SphericallySymmetricConfigurations/Virial#Normalizations|introductory discussion of the virial equilibrium of spherical configurations]]. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{ad}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{Hoerdt}} \biggl( \frac{R_\mathrm{Hoerdt}}{R_\mathrm{norm}} \biggr) | |||
\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~r_a \biggl[ \biggl(\frac{\gamma - 1}{\gamma}\biggr) (4\pi)^{\gamma-1}\biggr]^{1/(4-3\gamma)} | |||
\biggl[ 5 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_W \mathfrak{f}_M^{\gamma_g-2}} | |||
\biggr]^{1/(4-3\gamma_g)} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~r_a \biggl[ 5 \cdot 3^{\gamma-1} \biggl(\frac{\gamma - 1}{\gamma}\biggr) | |||
\frac{\mathfrak{f}_A \mathfrak{f}_M^{2-\gamma_g}}{\mathfrak{f}_W } | |||
\biggr]^{1/(4-3\gamma_g)} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
r_a \biggl[ \frac{5 \cdot 3^{1/n} }{n+1} \cdot \frac{\mathfrak{f}_A \mathfrak{f}_M^{(n-1)/n}}{\mathfrak{f}_W } \biggr]^{n/(n-3)} | |||
= r_a \biggl[ 3 \mathfrak{f}_M^{n-1} \biggl( \frac{5 }{n+1} \cdot \frac{\mathfrak{f}_A }{\mathfrak{f}_W }\biggr)^n \biggr]^{1/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad} \equiv \frac{P_\mathrm{e}}{P_\mathrm{ad}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{P_\mathrm{e}}{P_\mathrm{Hoerdt}} \biggl( \frac{P_\mathrm{Hoerdt}}{P_\mathrm{norm}} \biggr) | |||
\biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~p_a \biggl[ \biggl( \frac{\gamma}{\gamma-1}\biggr)^{3\gamma} (4\pi)^{-\gamma} \biggr]^{1/(4-3\gamma)} | |||
\biggl[ \mathfrak{f}_A^{-4} \biggl( \frac{4\pi}{3\cdot 5^3} \cdot \frac{\mathfrak{f}_W^3}{\mathfrak{f}_M^2} \biggr)^{\gamma_g} | |||
\biggr]^{1/(4-3\gamma_g)} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~p_a \mathfrak{f}_A^{-4/(4-3\gamma)} \biggl[ \biggl( \frac{\gamma}{\gamma-1}\biggr)^{3} | |||
\biggl( \frac{1}{3\cdot 5^3} \cdot \frac{\mathfrak{f}_W^3}{\mathfrak{f}_M^2} \biggr)\biggr]^{\gamma/(4-3\gamma)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~p_a \mathfrak{f}_A^{-4n/(n-3)} \biggl[ \frac{(n+1)^3}{3\cdot 5^3} \cdot \frac{\mathfrak{f}_W^3}{\mathfrak{f}_M^2} \biggr]^{(n+1)/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Now we insert the form-factor expressions [[User:Tohline/SSC/Virial/Polytropes#Summary|from above]], to obtain, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
r_a \biggl[ 3 \biggl( \frac{5 }{n+1} \biggr)^n \biggr]^{1/(n-3)} | |||
\biggl[ \frac{\mathfrak{f}_A^n \mathfrak{f}_M^{n-1} }{\mathfrak{f}_W^n } \biggr]^{1/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
r_a \biggl[ 3 \biggl( \frac{5 }{n+1} \biggr)^n \biggr]^{1/(n-3)} | |||
\biggl\{ | |||
\biggl[ \frac{3(n+1) }{(5-n)} ~( \Theta^' )^2 \biggr]^n | |||
\biggl[ \frac{3^2\cdot 5}{5-n} \biggl( \frac{\Theta^'}{\xi} \biggr)^2 \biggr]^{-n} | |||
\biggl[ - \frac{3\Theta^'}{\xi} \biggr]^{n-1} | |||
\biggr\}^{1/(n-3)}_{\xi_1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
r_a \biggl\{ 3^n \biggl( \frac{5 }{n+1} \biggr)^n \biggl[ \frac{3(n+1) }{(5-n)} \biggr]^n \biggl[ \frac{5-n}{3^2\cdot 5} \biggr]^{n} | |||
\biggr\}^{1/(n-3)} | |||
\biggl\{ \xi^{2n} | |||
\biggl[ - \frac{\Theta^'}{\xi} \biggr]^{n-1} | |||
\biggr\}^{1/(n-3)}_{\xi_1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
r_a \biggl[ \xi^{n+1} ( - \Theta^' )^{n-1} \biggr]^{1/(n-3)}_{\xi_1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~p_a \mathfrak{f}_A^{-4n/(n-3)} \biggl[ \frac{(n+1)^3}{3\cdot 5^3} \cdot \frac{\mathfrak{f}_W^3}{\mathfrak{f}_M^2} \biggr]^{(n+1)/(n-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~p_a \biggl[ \frac{3(n+1) }{(5-n)} ~( \Theta^' )^2 \biggr]_{\tilde\xi}^{-4n/(n-3)} | |||
\biggl\{ | |||
\frac{(n+1)^3}{3\cdot 5^3} \cdot | |||
\biggl[\frac{3^2\cdot 5}{5-n} \biggl( \frac{\Theta^'}{\xi} \biggr)^2\biggr]^3 | |||
\biggl[ - \frac{3\Theta^'}{\xi} \biggr]^{-2} | |||
\biggr\}^{(n+1)/(n-3)}_{\xi_1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~p_a \biggl\{ \biggl[ \frac{5-n}{3(n+1)} \biggr]^{4n} \biggl[ \frac{(n+1)^3 \cdot 3^6 \cdot 5^3}{3^3 \cdot 5^3 (5-n)^3} \biggr]^{(n+1)} \biggr\}^{1/(n-3)} | |||
\biggl[ ( \Theta^' )^{-8n} \biggl( \frac{\Theta^'}{\xi} \biggr)^{4(n+1)} | |||
\biggr]^{1/(n-3)}_{\xi_1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~p_a \biggl[ \frac{5-n}{3(n+1)} \biggr] \biggl[\xi^{n+1} ( \Theta^' )^{n-1} \biggr]^{-4/(n-3)}_{\xi_1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Notice that the bracketed term that is to be evaluated at <math>~\xi_1</math> is identical in both expressions. After [[User:Tohline/SSC/Virial/Polytropes#Renormalization|renormalization, as drived above]], the statement of virial equilibrium for embedded polytropes is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{ad}^4</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{\Pi_\mathrm{ad}} \biggl[ \chi_\mathrm{ad}^{4-3\gamma_g} - 1 \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or, setting <math>~\gamma_g = (n+1)/n</math>, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi_\mathrm{ad} \chi_\mathrm{ad}^4</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\chi_\mathrm{ad}^{(n-3)/n} - 1 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This relation can now be written in terms of [http://adsabs.harvard.edu/abs/1970MNRAS.151...81H Horedt's (1970)] dimensionless radius and pressure. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~p_a \biggl[ \frac{5-n}{3(n+1)} \biggr] \biggl[\xi^{n+1} ( \Theta^' )^{n-1} \biggr]^{-4/(n-3)}_{\xi_1} | |||
\cdot r_a^4 \biggl[ \xi^{n+1} ( - \Theta^' )^{n-1} \biggr]^{4/(n-3)}_{\xi_1} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ r_a^{(n-3)/n} \biggl[ \xi^{n+1} ( - \Theta^' )^{n-1} \biggr]^{1/n}_{\xi_1} - 1</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
\Rightarrow ~~~~ p_a r_a^4 \biggl[ \frac{5-n}{3(n+1)} \biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ r_a^{(n-3)/n} \biggl[ \xi^{n+1} ( - \Theta^' )^{n-1} \biggr]^{1/n}_{\xi_1} - 1 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, from our separate [[User:Tohline/SSC/Structure/PolytropesEmbedded#Horedt.27s_Presentation|summary of Hoerdt's presentation]], | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~r_a | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} | |||
= \biggl[ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} \biggr]^{-1/(n-3)}\, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~p_a | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, the virial relation becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
~1 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl\{ \frac{ [ \xi^{n+1} ( - \Theta^' )^{n-1} ]_{\xi_1} }{ [ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} ] } | |||
\biggr\}^{1/n} | |||
- \biggl[ \frac{5-n}{3(n+1)} \biggr] \tilde\theta_n^{n+1} \biggl\{ \frac{( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)}}{ | |||
[ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} ]^{4/(n-3)} } \biggr\} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ \frac{ \xi_1^{n+1} ( - \Theta^' )^{n-1}_{\xi_1} }{ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} } | |||
\biggr]^{1/n} | |||
- \biggl[ \frac{5-n}{3(n+1)} \biggr] \tilde\theta_n^{n+1} \biggl\{ \frac{ \tilde\xi^{4n+4} ( -\tilde\theta' )^{2n+2}}{ | |||
\tilde\xi^{4n+4} (-\tilde\theta^')^{4n-4} } \biggr\}^{1/(n-3)} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ \frac{ \xi_1^{n+1} ( - \Theta^' )^{n-1}_{\xi_1} }{ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} } | |||
\biggr]^{1/n} | |||
- \biggl[ \frac{5-n}{3(n+1)} \biggr] \frac{ \tilde\theta_n^{n+1} }{ ( -\tilde\theta' )^{2} } \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
This needs to be checked, perhaps with specific applications to the cases <math>~n=1</math> and <math>~n=5</math>. | |||
= | =See Also= | ||
<ul> | |||
<li>[[User:Tohline/SphericallySymmetricConfigurations/IndexFreeEnergy#Index_to_Free-Energy_Analyses|Index to a Variety of Free-Energy and/or Virial Analyses]]</li> | |||
</ul> | |||
</ | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Latest revision as of 16:52, 12 August 2016
Virial Equilibrium of Adiabatic Spheres
Highlights of the rather detailed discussion presented below have been summarized in an accompanying chapter of this H_Book.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Review
Adopted Normalizations
In an introductory discussion of the virial equilibrium structure of spherically symmetric configurations, we adopted the following physical parameter normalizations for adiabatic systems.
|
Adopted Normalizations for Adiabatic Systems | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||
Virial Equilibrium
Also in our introductory discussion — see especially the section titled, Energy Extrema — we deduced that an adiabatic system's dimensionless equilibrium radius,
<math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \, ,</math>
is given by the root(s) of the following equation:
<math> 2C \chi_\mathrm{eq}^{-2} + ~3 B\chi_\mathrm{eq}^{3 -3\gamma_g} -~3A\chi_\mathrm{eq}^{-1} -~ 3D \chi_\mathrm{eq}^3 = 0 \, , </math>
where the definitions of the various coefficients are,
|
<math>~A</math> |
<math>~\equiv</math> |
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \, ,</math> |
|
<math>~B</math> |
<math>~\equiv</math> |
<math> \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} \cdot \mathfrak{f}_A </math> |
|
|
<math>~=</math> |
<math> \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \cdot \mathfrak{f}_A \, , </math> |
|
<math>~C</math> |
<math>~\equiv</math> |
<math> \frac{3\cdot 5}{2^4 \pi} \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \cdot \frac{\mathfrak{f}_T}{\mathfrak{f}_M} \, , </math> |
|
<math>~D</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, . </math> |
(The dimensionless structural form factors, <math>~\mathfrak{f}_i,</math> that appear in these expressions are defined for isolated polytropes in our accompanying introductory discussion and are discussed further, below.) Once the pressure exerted by the external medium (<math>~P_e</math>), and the configuration's mass (<math>~M_\mathrm{tot}</math>), angular momentum (<math>~J</math>), and specific entropy (via <math>~K</math>) have been specified, the values of all of the coefficients are known and <math>~\chi_\mathrm{eq}</math> can be determined.
Isolated Nonrotating Adiabatic Configuration
For a nonrotating configuration <math>~(C=J=0)</math> that is not influenced by the effects of a bounding external medium <math>~(D=P_e = 0)</math>, the statement of virial equilibrium is,
<math> 3 B\chi_\mathrm{eq}^{3 -3\gamma_g} -~3A\chi_\mathrm{eq}^{-1} = 0 \, . </math>
Hence, one equilibrium state exists for each value of <math>~\gamma_g</math> and it occurs where,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_g} = \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{4-3\gamma_g} </math> |
<math>~=</math> |
<math> \frac{A}{B} \, . </math> |
|
Two Points of View |
||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
In terms of <math>~K</math> and <math>~M_\mathrm{limit} ~(= M_\mathrm{tot})</math> |
In terms of <math>~P_c</math> and <math>~M_\mathrm{limit} ~(= M_\mathrm{tot})</math> |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
According to the solution shown in the left-hand column, for fluid with a given specify entropy content, the equilibrium mass-radius relationship for adiabatic configurations is,
<math> M_\mathrm{tot}^{(\gamma_g - 2)} \propto R_\mathrm{eq}^{(3\gamma_g -4)} \, . </math>
We see that, for <math>~\gamma_g=2</math>, the equilibrium radius depends only on the specific entropy of the gas and is independent of the configuration's mass. Conversely, for <math>~\gamma_g = 4/3</math>, the mass of the configuration is independent of the radius. For <math>~\gamma_g > 2</math> or <math>~\gamma_g < 4/3</math>, configurations with larger mass (but the same specific entropy) have larger equilibrium radii. However, for <math>~\gamma_g</math> in the range, <math>~2 > \gamma_g > 4/3</math>, configurations with larger mass have smaller equilibrium radii. (Note that the related result for isothermal configurations can be obtained by setting <math>~\gamma_g = 1</math> in this adiabatic solution, because <math>~K = c_s^2</math> when <math>~\gamma_g = 1</math>.)
Role of Structural Form Factors
When employing a virial analysis to determine the radius of an equilibrium configuration, it is customary to set the structural form factors, <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_A</math>, to unity and accept that the expression derived for <math>~R_\mathrm{eq}</math> is an estimate of the configuration's radius that is good to within a factor of order unity. As has been demonstrated in our related discussion of the equilibrium of uniform-density spheres, these form factors can be evaluated if/when the internal structural profile of an equilibrium configuration is known from a complementary detailed force-balance analysis. In the case being discussed here of isolated, spherical polytropes, solutions to the,
Lane-Emden Equation
|
<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math> |
can provide the desired internal structural information. Here we draw on Chandrasekhar's [C67] discussion of the structure of spherical polytropes to show precisely how our structural form factors can be expressed in terms of the Lane-Emden function, <math>~\Theta_H</math>, dimensionless radial coordinate, <math>~\xi</math>, and the function derivative, <math>~\Theta^' = d\Theta_H/d\xi</math>.
Mass
We note, first, that Chandrasekhar [C67] — see his Equation (78) on p. 99 — presents the following expression for the mean-to-central density ratio:
|
<math>~\frac{\bar\rho}{\rho_c}</math> |
<math>~=</math> |
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\xi_1} \, ,</math> |
where the notation at the bottom of the closing square bracket means that everything inside the square brackets should be, "evaluated at the surface of the configuration," that is, at the radial location, <math>~\xi_1</math>, where the Lane-Emden function, <math>~\Theta_H(\xi)</math>, first goes to zero. But, as we pointed out when defining the structural form factors, the form factor associated with the configuration mass, <math>~\mathfrak{f}_M</math>, is equivalent to the mean-to-central density ratio. We conclude, therefore, that,
|
<math>~\mathfrak{f}_M</math> |
<math>~=</math> |
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\xi_1} \, .</math> |
Gravitational Potential Energy
Second, we note that Chandrasekhar's [C67] expression for the gravitational potential energy — see his Equation (90), p. 101 — is,
|
<math>~-W</math> |
<math>~=</math> |
<math>~\frac{3}{5-n} \biggl( \frac{GM^2}{R} \biggr) \, ,</math> |
whereas our analogous expression is,
|
<math>~-W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~\frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \, .</math> |
We conclude, therefore, that,
|
<math>~\frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} </math> |
<math>~=</math> |
<math>~\frac{5}{5-n} </math> |
|
<math>\Rightarrow ~~~~\mathfrak{f}_W </math> |
<math>~=</math> |
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\xi_1} \, .</math> |
Mass-Radius Relationship
Third, Chandrasekhar [C67] shows — see his Equation (72), p. 98 — that the general mass-radius relationship for isolated spherical polytropes is,
|
<math>~GM^{(n-1)/n} R^{(3-n)/n}</math> |
<math>~=</math> |
<math> ~\frac{(n+1)K}{(4\pi)^{1/n}} \biggl[ - \xi^{(n+1)/(n-1)} \frac{d\Theta_H}{d\xi} \biggr]^{(n-1)/n}_{\xi=\xi_1} \, , </math> |
which we choose to rewrite as,
|
<math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R^{(3-n)}</math> |
<math>~=</math> |
<math> ~(n+1)^n\biggl[ \xi^{(n+1)} (-\Theta^')^{(n-1)}\biggr]_{\xi=\xi_1} </math> |
|
|
<math>~=</math> |
<math> - \biggl( \frac{\xi}{\Theta^'} \biggr)_{\xi=\xi_1} \biggl[ (n+1) \xi ~(-\Theta^') \biggr]^n_{\xi=\xi_1} \, . </math> |
By comparison, the expression for the equilibrium radius that has been derived, above, from an analysis of extrema in the free energy function — specifically, see the last expression in the left-hand column of the table titled "Two Points of View" — we obtain,
|
<math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R_\mathrm{eq}^{(3-n)}</math> |
<math>~=</math> |
<math> ~\frac{3}{\mathfrak{f}_M} \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr)^n \, . </math> |
Hence, it appears as though, quite generally,
|
<math>~ \frac{1}{\mathfrak{f}_M} \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr)^n </math> |
<math>~=</math> |
<math> - \biggl( \frac{\xi}{3\Theta^'} \biggr)_{\xi=\xi_1} \biggl[ (n+1) \xi ~(-\Theta^') \biggr]^n_{\xi=\xi_1} \, . </math> |
Or, taking into account the expressions for <math>~\mathfrak{f}_M</math> and <math>~\mathfrak{f}_W</math> that have just been uncovered, we conclude that,
|
<math>~ \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} </math> |
<math>~=</math> |
<math> \biggl[ (n+1) \xi ~(-\Theta^') \biggr]_{\xi=\xi_1} </math> |
|
<math>\Rightarrow ~~~~ \frac{\mathfrak{f}_A}{\mathfrak{f}_W} </math> |
<math>~=</math> |
<math> \frac{(n+1) }{3\cdot 5} ~\xi_1^2 \, . </math> |
|
<math>\Rightarrow ~~~~ \mathfrak{f}_A </math> |
<math>~=</math> |
<math> \frac{(n+1) }{3\cdot 5} ~\xi_1^2 \biggl\{ \frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\xi_1} \biggr\}\, . </math> |
|
|
<math>~=</math> |
<math> \frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\xi_1} \, . </math> |
Central Pressure
It is also worth pointing out that Chandrasekhar [C67] — see his Equations (80) & (81), p. 99 — introduces a dimensionless structural form factor, <math>~W_n</math>, for the central pressure via the expression,
|
<math>~P_c</math> |
<math>~=</math> |
<math>~W_n \biggl( \frac{GM^2}{R^4} \biggr) \, ,</math> |
and demonstrates that,
|
<math>~\frac{1}{W_n}</math> |
<math>~\equiv</math> |
<math>~4\pi (n+1) \biggl[ \Theta^' \biggr]^2_{\xi_1} \, .</math> |
It is therefore clear that a spherical polytrope's central pressure is expressible in terms of our structural form factor, <math>~\mathfrak{f}_A</math>, as,
|
<math>~P_c</math> |
<math>~=</math> |
<math>~\frac{3}{4\pi (5-n)} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) \frac{1}{\mathfrak{f}_A} \, .</math> |
Alternate Derivation of Gravitational Potential Energy
As has been discussed elsewhere, we have learned from Chandrasekhar's discussion of polytropic spheres [C67] — see his Equation (16), p. 64 — that if a spherically symmetric system is in hydrostatic balance, the total gravitational potential energy can be obtained from the following integral:
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ + \frac{1}{2} \int_0^R \Phi(r) dm \, .</math> |
Using "technique #3" to solve the differential equation that governs the statement of hydrostatic balance, we know that in any polytropic sphere, <math>~\Phi(r)</math> is related to the configuration's radial enthalpy profile, <math>~H(r)</math>, via the algebraic expression,
|
<math>~\Phi(r) + H(r)</math> |
<math>~=</math> |
<math>~C_B \, ,</math> |
where, <math>~C_B</math>, is an integration constant. At the surface of the equilibrium configuration, <math>~H = 0</math> and <math>~\Phi = - GM_\mathrm{tot}/R_\mathrm{eq}</math>, so the integration constant is,
|
<math>~C_B</math> |
<math>~=</math> |
<math>~- \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, ,</math> |
which implies,
|
<math>~\Phi(r) </math> |
<math>~=</math> |
<math>~ - H(r) - \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, .</math> |
Now, from our general discussion of barotropic relations, we can write,
|
<math>~H(r)</math> |
<math>~=</math> |
<math>~(n+1) \frac{P(r)}{\rho(r)} \, .</math> |
Hence,
|
<math>~-\Phi(r)</math> |
<math>~=</math> |
<math>~(n+1) \frac{P(r)}{\rho(r)} + \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, ,</math> |
and,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ - \frac{1}{2} \int_0^R \biggl[ (n+1) \frac{P(r)}{\rho(r)} + \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \biggr] 4\pi \rho(r) r^2 dr </math> |
|
|
<math>~=</math> |
<math>~ - 2\pi \biggl\{ (n+1) \int_0^R P(r) r^2 dr + \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \int_0^R \rho(r) r^2 dr \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - 2\pi \biggl\{ \frac{1}{3} (n+1)P_c R_\mathrm{eq}^3 \int_0^1 3\biggl[ \frac{P(x)}{P_c} \biggr] x^2 dx + \frac{GM_\mathrm{tot}}{3R_\mathrm{eq}} \biggl( \rho_c R_\mathrm{eq}^3 \biggr) \int_0^1 3 \biggl[ \frac{\rho(x)}{\rho_c} \biggr] x^2 dx \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - 2\pi \biggl\{ \frac{1}{3} (n+1)P_c R_\mathrm{eq}^3 \mathfrak{f}_A + \frac{GM_\mathrm{tot}}{3R_\mathrm{eq}} \biggl( \rho_c R_\mathrm{eq}^3 \biggr) \mathfrak{f}_M \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggl\{ \frac{2\pi}{3} (n+1) \biggl[ \frac{P_c R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} \biggr] \mathfrak{f}_A + \frac{1}{2} \biggl[ \frac{4\pi \rho_c R_\mathrm{eq}^3}{3M_\mathrm{tot}} \biggr] \mathfrak{f}_M \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \frac{1}{2} \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggl\{ \frac{4\pi}{3} (n+1) \biggl[ \frac{P_c R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} \biggr] \mathfrak{f}_A + 1 \biggr\} \, .</math> |
We now recall two earlier expressions that show the role that our structural form factors play in the evaluation of <math>~W_\mathrm{grav}</math> and <math>~P_c</math>, namely,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ - \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggr) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
and,
|
<math>~P_c</math> |
<math>~=</math> |
<math>~ \frac{3 }{20\pi }\biggl( \frac{G M_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \mathfrak{f}_M^2} \, .</math> |
Plugging these into our newly derived expression for the gravitational potential energy gives,
|
<math>~- \frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
<math>~=</math> |
<math>~ - \frac{1}{2} \biggl\{ \frac{4\pi}{3} (n+1) \biggl[ \frac{3 }{20\pi }\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \mathfrak{f}_M^2} \biggr] \mathfrak{f}_A + 1 \biggr\} </math> |
|
<math>\Rightarrow ~~~~ (2\cdot 3) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
<math>~=</math> |
<math>~ (n+1) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} + 5 </math> |
|
<math>\Rightarrow ~~~~ (5 - n) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
<math>~=</math> |
<math>~ 5 </math> |
|
<math>\Rightarrow ~~~~ \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
<math>~=</math> |
<math>~ \frac{5}{5-n} \, . </math> |
As it should, this agrees with the expression for the ratio, <math>\mathfrak{f}_W/\mathfrak{f}_M^2</math>, that was derived in our above discussion of the gravitational potential energy.
Summary
In summary, expressions for the three structural form factors associated with isolated, spherically symmetric polytropes are as follows:
|
Structural Form Factors for Isolated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
Nonrotating Adiabatic Configuration Embedded in an External Medium
For a nonrotating configuration <math>~(C=J=0)</math> that is embedded in, and is influenced by the pressure <math>~P_e</math> of, an external medium, the statement of virial equilibrium is,
<math> 3 B\chi_\mathrm{eq}^{3 -3\gamma_g} -~3A\chi_\mathrm{eq}^{-1} -~ 3D\chi_\mathrm{eq}^3 = 0 \, . </math>
Solution Expressed in Terms of K and M (Whitworth's 1981 Relation)
This is precisely the same condition that derives from setting equation (3) to zero in Whitworth's (1981, MNRAS, 195, 967) discussion of the Global Gravitational Stability for One-dimensional Polytropes. The overlap with Whitworth's narative is clearer after introducing the algebraic expressions for the coefficients <math>~A</math>, <math>~B</math>, and <math>~D</math>, to obtain,
|
<math>~4\pi \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^3 </math> |
<math>~=</math> |
<math>~3 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot \chi_\mathrm{eq}^{3 -3\gamma_g} ~-~\frac{3}{5} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \cdot \chi_\mathrm{eq}^{-1} \, ;</math> |
dividing the equation through by <math>~(4\pi \chi_\mathrm{eq}^3/P_\mathrm{norm})</math>,
|
<math>~P_e </math> |
<math>~=</math> |
<math>~P_\mathrm{norm} \biggl[ \biggl( \frac{3}{4\pi} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot \chi_\mathrm{eq}^{-3\gamma_g} ~- \biggl(\frac{3}{20\pi} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \cdot \chi_\mathrm{eq}^{-4} \biggr] </math> |
|
|
<math>~=</math> |
<math>~P_\mathrm{norm} R_\mathrm{norm}^4\biggl[ \biggl( \frac{3}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot R_\mathrm{norm}^{3\gamma_g-4} - \biggl(\frac{3}{20\pi R_\mathrm{eq}^4} \biggr)\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \biggr] \, ;</math> |
and inserting expressions for the parameter normalizations as defined in our accompanying introductory discussion to obtain,
|
<math>~P_e </math> |
<math>~=</math> |
<math>~GM_\mathrm{tot}^2\biggl[ \biggl( \frac{3}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot \frac{K M_\mathrm{tot}^{\gamma_g-2}}{G} - \biggl(\frac{3}{20\pi R_\mathrm{eq}^4} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \biggr] </math> |
|
|
<math>~=</math> |
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} - \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, .</math> |
If the structural form factors are set equal to unity, this exactly matches equation (5) of Whitworth, which reads:
|
Equation and accompanying sentence extracted without modification from p. 970 of Whitworth (1981)
"Global Gravitational Stability for One-dimensional Polytropes"
Monthly Notices of the Royal Astronomical Society, vol. 195, pp. 967-977 © Royal Astronomical Society |
Notice that, when <math>~P_e \rightarrow 0</math>, this expression reduces to the solution we obtained for an isolated polytrope, expressed in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math> (see the left-hand column of our table titled "Two Points of View").
Solution Expressed in Terms of M and Central Pressure
Beginning again with the relevant statement of virial equilibrium, namely,
<math> A = B\chi_\mathrm{eq}^{4 -3\gamma_g} -~ D\chi_\mathrm{eq}^4 \, , </math>
but adopting the alternate expression for the coefficient, <math>~B</math>, given above, that is,
<math> B = \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \cdot \mathfrak{f}_A \, , </math>
we can write,
|
<math>~\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \mathfrak{f}_A \cdot \chi_\mathrm{eq}^{4 -3\gamma_g} -~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \chi_\mathrm{eq}^4 </math> |
|
<math>~\Rightarrow~~~\frac{3}{20\pi} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \mathfrak{f}_A -~ \frac{P_e}{P_\mathrm{norm}} \biggr] \chi_\mathrm{eq}^4 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \mathfrak{f}_A P_c -~ P_e\biggr] \frac{R_\mathrm{eq}^4}{G M_\mathrm{tot}^2} </math> |
|
<math>\Rightarrow ~~~ \frac{3}{20\pi} \biggl( \frac{G M_\mathrm{limit}^2}{R_\mathrm{eq}^4}\biggr) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} </math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A P_c -~ P_e \, . </math> |
Again notice that, when <math>~P_e \rightarrow 0</math>, this expression reduces to the solution we obtained for an isolated polytrope, but this time expressed in terms of <math>~P_c</math> and <math>~M_\mathrm{limit}</math> (see the right-hand column of our table titled "Two Points of View").
Contrast with Detailed Force-Balanced Solution
As has just been demonstrated, the virial theorem provides a mathematical expression that allows us to relate the equilibrium radius of a configuration to the applied external pressure, once the configuration's mass and either its specific entropy or central pressure are specified. In contrast to this, as has been discussed in detail in another chapter, Horedt (1970), Whitworth (1981) and Stahler (1983) have each derived separate analytic expressions for <math>~R_\mathrm{eq}</math> and <math>~P_e</math> — given in terms of the Lane-Emden function, <math>~\Theta</math>, and its radial derivative — without demonstrating how the equilibrium radius and external pressure directly relate to one another. That is to say, solution of the detailed force-balanced equations provides a pair of equilibrium expressions that are parametrically related to one another through the Lane-Emden function. For example — see our related discussion for more details — Horedt derives the following set of parametric equations relating the configuration's dimensionless radius, <math>~r_a</math>, to a specified dimensionless bounding pressure, <math>~p_a</math>:
|
<math> ~r_a \equiv \frac{R_\mathrm{eq}}{R_\mathrm{Horedt}} </math> |
<math>~=~</math> |
<math> \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \, , </math> |
|
<math> ~p_a \equiv \frac{P_\mathrm{e}}{P_\mathrm{Horedt}} </math> |
<math>~=~</math> |
<math> \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \, , </math> |
where,
|
<math> ~R_\mathrm{Horedt} </math> |
<math>~=</math> |
<math> \biggl[ \frac{4\pi}{(n+1)^n}\biggl( \frac{G}{K} \biggr)^n M_\mathrm{limit}^{n-1} \biggr]^{1/(n-3)} \, , </math> |
|
<math> ~P_\mathrm{Horedt} </math> |
<math>~=</math> |
<math> K^{4n/(n-3)}\biggl[ \frac{(n+1)^3}{4\pi G^3 M_\mathrm{limit}^2} \biggr]^{(n+1)/(n-3)} \, . </math> |
It is important to appreciate that, in the expressions for <math>~r_a</math> and <math>~p_a</math>, the tilde indicates that the Lane-Emden function and its derivative are to be evaluated, not at the radial coordinate, <math>~\xi_1</math>, that is traditionally associated with the "first zero" of the Lane-Emden function and therefore with the surface of the isolated polytrope, but at the radial coordinate, <math>~\tilde\xi</math>, where the internal pressure of the isolated polytrope equals <math>~P_e</math> and at which the embedded polytrope is to be truncated. The coordinate, <math>~\tilde\xi</math>, therefore identifies the surface of the embedded — or, pressure-truncated — polytrope. We also have taken the liberty of attaching the subscript "limit" to <math>~M</math> in both defining relations because it is clear that Hoerdt intended for the normalization mass to be the mass of the pressure-truncated object, not the mass of the associated isolated (and untruncated) polytrope. In anticipation of further derivations, below, we note here the ratio of Hoerdt's normalization parameters to ours, assuming <math>~\gamma = (n+1)/n</math>:
|
<math>~\biggl( \frac{R_\mathrm{Hoerdt}}{R_\mathrm{norm}} \biggr)^{n-3}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{4\pi}{(n+1)^n}\biggl( \frac{G}{K} \biggr)^n M_\mathrm{limit}^{n-1} \biggr] \biggl[ \biggl( \frac{K}{G}\biggr)^n M_\mathrm{tot}^{1-n}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} \, , </math> |
|
<math>~\biggl( \frac{P_\mathrm{Hoerdt}}{P_\mathrm{norm}} \biggr)^{n-3}</math> |
<math>~=</math> |
<math>~ K^{4n}\biggl[ \frac{(n+1)^3}{4\pi G^3 M_\mathrm{limit}^2} \biggr]^{n+1} \biggl[ \frac{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}}{K^{4n}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{n+1} \, . </math> |
Next, we demonstrate that this pair of parametric relations satisfies the virial theorem and, in so doing, demonstrate how <math>~r_a</math> and <math>~p_a</math> may be directly related to each other. Given that Hoerdt's chosen normalization radius and normalization pressure are defined in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math>, we begin with the virial theorem derived above in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math>, setting <math>~\gamma_g = (n+1)/n</math>.
|
<math>~P_e </math> |
<math>~=</math> |
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{(n+1)/n}} - \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, .</math> |
After setting <math>~R_\mathrm{eq} = r_a R_\mathrm{Horedt} </math>, a bit of algebraic manipulation shows that the first term on the right-hand side of the virial equilibrium expression becomes,
|
<math>~ K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{(n+1)/n}} </math> |
<math>~=</math> |
<math>~ r_a^{-3(n+1)/n} \mathfrak{f}_A \biggl[ \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{n-3} \frac{(n+1)^{3n}}{(4\pi)^n}\biggr]^{(n+1)/[n(n-3)]} [K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, , </math> |
while the second term on the right-hand side becomes,
|
<math>~ \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} </math> |
<math>~=</math> |
<math>~ \frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} (4\pi)^{-(n+1)/(n-3)} (n+1)^{4n/(n-3)}~ [K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, . </math> |
But, using Horedt's expression for <math>~P_e</math>, the left-hand side of the virial equilibrium equation becomes,
|
<math>~P_e = p_a P_\mathrm{Hoerdt}</math> |
<math>~=</math> |
<math>~ p_a~(4\pi)^{-(n+1)/(n-3)} ~(n+1)^{3(n+1)/(n-3)} [K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, . </math> |
Hence, the statement of virial equilibrium is,
|
<math>~ p_a~ </math> |
<math>~=</math> |
<math>~ \biggr\{ r_a^{-3(n+1)/n} \mathfrak{f}_A \biggl[ \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{n-3} \frac{(n+1)^{3n}}{(4\pi)^n}\biggr]^{(n+1)/[n(n-3)]} </math> |
|
|
|
<math>~~ - \frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} (4\pi)^{-(n+1)/(n-3)} (n+1)^{4n/(n-3)} \biggr\}(4\pi)^{(n+1)/(n-3)} ~(n+1)^{-3(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M \cdot r_a^3} \biggr)^{(n+1)/n} - \frac{3(n+1)}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} \, ; </math> |
or, multiplying through by <math>~r_a^4</math> and rearranging terms,
|
Now, Hoerdt has given analytic expressions for <math>~r_a</math> and <math>~p_a</math> in terms of the Lane-Emden function and its first derivative. The question is, what should the expressions for our structural form factors be in order for this virial expression to hold true for all pressure-truncated polytropic structures? As has been summarized above, in the case of an isolated polytrope, whose surface is located at <math>~\xi_1</math> and whose global properties are defined by evaluation of the Lane-Emden function at <math>~\xi_1</math>, we know that (see the above summary),
|
Structural Form Factors for Isolated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
These same expressions may or may not work for pressure-truncated polytropes, even if the evaluation radius is shifted from <math>~\xi_1</math> to <math>~\tilde\xi</math>. Let's see …
January 13, 2015: As is noted in our accompanying outline of work, I no longer believe that <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_A</math> have the same expressions as in isolated polytropes. Hence, all of the material that follows is suspect and needs to be reworked.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Inserting Hoerdt's expressions for <math>~r_a</math> and <math>~p_a</math> into the viral equilibrium expression, we have,
|
<math>~ \frac{3(n+1)}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} </math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{(n-3)/n} ~-~ \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{4} </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{(n-3)/n} ~-~ \tilde\theta_n^{n+1} \tilde\xi^4 [( -\tilde\xi^2 \tilde\theta' )^{2(n+1)+4(1-n)} ]^{1/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi^{(n-3)} ( -\tilde\xi^2 \tilde\theta' )^{(1-n)} ]^{1/n} ~-~ \tilde\theta_n^{n+1} \tilde\xi^4 [( -\tilde\xi^2 \tilde\theta' )^{-2} ] </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} \tilde\xi^{-(n+1)/n} ( -\tilde\theta' )^{(1-n)/n} ~-~ \frac{\tilde\theta_n^{n+1} }{( -\tilde\theta' )^{2} } \, . </math> |
If we assume that both of the structural form factors, <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_M</math>, have the same functional expressions as in the case of isolated polytropes (but evaluated at <math>~\tilde\xi</math> instead of at <math>~\xi_1</math>), the virial relation further reduces to the form,
|
<math>~ \frac{\tilde\theta_n^{n+1} }{( -\tilde\theta' )^{2} } </math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{\tilde\xi}{- \tilde\theta'} \biggr)^{(n+1)/n} \tilde\xi^{-(n+1)/n} ( -\tilde\theta' )^{(1-n)/n} - \frac{3(n+1)}{5-n} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\mathfrak{f}_A}{(- \tilde\theta' )^2} - \frac{3(n+1)}{5-n}
</math> |
|
<math>~ \Rightarrow~~~\mathfrak{f}_A </math> |
<math>~=</math> |
<math>~ \frac{3(n+1)}{5-n} (- \tilde\theta' )^2 + \tilde\theta_n^{n+1} \, . </math> |
This all seems to make a great deal of sense. Only the structural parameter that is derived from an integral over the pressure distribution, <math>~\mathfrak{f}_A</math>, gets modified when the polytropic configuration is truncated. Notice, as well, that the term that has been added to the definition of <math>~\mathfrak{f}_A</math> naturally goes to zero in the limit of <math>~\tilde\xi \rightarrow \xi_1</math>, that is, for an isolated polytrope. We should definitely go back to the original definitions of all three structural parameters and prove that this is the case. But, in the meantime, here is the summary:
|
WRONG!! For the correct form-factor expressions, go here. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
Structural Form Factors for Pressure-Truncated Polytropes | |||||||||
|
WRONG!! For the correct form-factor expressions, go here.
Notice that, in an effort to differentiate them from their counterparts developed earlier for "isolated" polytropes, we have affixed a tilde to each of these three form-factors, <math>~\mathfrak{f}_i</math>.
Example
Outline
Let's identify an equilibrium configuration numerically, using the free-energy expression. From our introductory discussion, the relevant expression is,
<math> \mathfrak{G}^* = -3\mathcal{A} \chi^{-1} -~ \frac{1}{(1-\gamma_g)} \mathcal{B} \chi^{3-3\gamma_g} +~ \mathcal{D}\chi^3 \, , </math>
where,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math> \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} \cdot \mathfrak{f}_A </math> |
|
|
<math>~=</math> |
<math> \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \cdot \mathfrak{f}_A \, , </math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, . </math> |
|
For later use, note that,
and,
|
Now, we could just blindly start setting values of the three leading coefficients, <math>~\mathcal{A}</math>, <math>~\mathcal{B}</math>, and <math>~\mathcal{D}</math>, then plot <math>~\mathfrak{G}^*(\chi)</math> to look for extrema. But let's accept a little guidance from this chapter's virial analysis before choosing the coefficient values. For embedded polytropes, we know that the structural form factors are,
|
<math>~\tilde\mathfrak{f}_M = \frac{\bar\rho}{\rho_c}</math> |
<math>~=</math> |
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\tilde\xi} \, ,</math> |
|
<math>\tilde\mathfrak{f}_W </math> |
<math>~=</math> |
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\tilde\xi} = \biggl( \frac{5}{5-n} \biggr) \tilde\mathfrak{f}_M^2 \, ,</math> |
|
<math>\tilde\mathfrak{f}_A = \frac{\bar{P}}{P_c}</math> |
<math>~=</math> |
<math> \frac{3(n+1) }{(5-n)} ~\biggl( \Theta^' \biggr)^2_{\tilde\xi} + \tilde\Theta^{n+1} \, . </math> |
Hence, the coefficient expressions become,
|
<math>~\mathcal{A}</math> |
<math>~=</math> |
<math>\frac{1}{(5-n)} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~=</math> |
<math> \frac{4\pi}{3} \biggl( \frac{\bar{P}}{P_\mathrm{norm}} \biggr)\chi^{3(n+1)/n}_\mathrm{eq} \, , </math> |
|
<math>~\mathcal{D}</math> |
<math>~=</math> |
<math> \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, . </math> |
Strategy
Generic setup:
- Choose the polytropic index, <math>~n</math>, which also sets the value of the adiabatic index, <math>~\gamma=(n+1)/n</math>.
- Fix <math>~M_\mathrm{tot}</math> and <math>~K</math>, so that the radial and pressure normalizations are fixed; specifically,
|
<math>~R_\mathrm{norm}^{n-3} = \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} </math> |
and |
<math>~P_\mathrm{norm}^{(n-3)} = K^{4n} (G^3 M_\mathrm{tot}^2)^{-(n+1)} \, .</math> |
- Fix <math>~M_\mathrm{limit}</math>, and let it be the normalization mass; that is, set <math>~M_\mathrm{limit} = M_\mathrm{tot}</math>.
- As a result of the above choices, the value of <math>~\mathcal{A}</math> is set, and fixed; specifically,
<math>~A = \frac{1}{(5-n)} \, .</math>
Case I:
- Fix <math>~\mathcal{D}</math>, which fixes the external pressure; specifically,
<math>~P_e = \frac{3}{4\pi} \cdot \mathcal{D} P_\mathrm{norm} \, .</math>
- Choose a variety of values of the remaining coefficient, <math>~\mathcal{B}</math>; then, for each value, plot <math>\mathfrak{G}^*(\chi)</math> and locate one or more extrema along with the value of <math>~\chi_\mathrm{eq}</math> that is associated with each free energy extremum. This identifies the equilibrium value of the mean pressure inside the pressure-truncated polytrope via the expression,
<math>~ \bar{P} = \biggl(\frac{3}{4\pi} \biggr) P_\mathrm{norm}~\mathcal{B} ~\chi^{-3(n+1)/n}_\mathrm{eq} \, .</math>
- In order to check whether we've identified the correct value of <math>~\chi_\mathrm{eq}</math>, we have to relate it to the radial coordinate, <math>~\xi_e</math>, used in the analytic solution of the Lane-Emden equation. As has been explained in our discussion of detailed force-balanced models of polytropes, generically,
|
<math>~R_\mathrm{eq} </math> |
<math>~=</math> |
<math>~a_n \xi_e \, ,</math> where, |
|
<math>~a_\mathrm{n} </math> |
<math>~\equiv</math> |
<math>~ \biggl[\frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr)\biggr]^{1/2} = \biggl[ \frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n}\biggr]^{1/2} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{a_n}{R_\mathrm{norm}} \biggr)^2</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n+1) K }{4\pi G} \biggr] \rho_c^{(1-n)/n} \cdot \frac{1}{R_\mathrm{norm}^2}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{(n+1) K }{4\pi G} \biggr] \biggl( \frac{\rho_c}{\bar\rho} \biggr)^{(1-n)/n} \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(1-n)/n} \cdot \frac{1}{R_\mathrm{norm}^2} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{(n+1) K }{4\pi G} \biggr] \biggl( \frac{\rho_c}{\bar\rho} \biggr)^{(1-n)/n} \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr)^{(1-n)/n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{(1-n)/n} \chi_\mathrm{eq}^{3(n-1)/n} \cdot R_\mathrm{norm}^{(n-3)/n} </math> |
|
|
<math>~=</math> |
<math>~\frac{(n+1) }{4\pi } \biggl[ \frac{3}{4\pi}\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(1-n)/n} \chi_\mathrm{eq}^{3(n-1)/n} \, . </math> |
Hence,
|
<math>~\xi_e^2</math> |
<math>~=</math> |
<math>~\biggl( \frac{R_\mathrm{eq}}{a_n} \biggr)^2 = \chi_\mathrm{eq}^2 \biggl( \frac{a_n}{R_\mathrm{norm}} \biggr)^{-2}</math> |
|
|
<math>~=</math> |
<math>~\chi_\mathrm{eq}^2 \biggl\{ \frac{4\pi }{(n+1) } \biggl[ \frac{3}{4\pi}\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n-1)/n} \chi_\mathrm{eq}^{3(1-n)/n} \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{4\pi }{(n+1) } \biggl[ \frac{3}{4\pi}\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^{(n-1)/n} \chi_\mathrm{eq}^{(3-n)/n} \, . </math> |
But, from above, we also know that,
|
<math>~\frac{3}{4\pi}\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{3\mathcal{B}}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_A} \biggr]^{n/(n+1)} \, ,</math> |
where,
|
<math>\tilde\mathfrak{f}_A = \frac{\bar{P}}{P_c}</math> |
<math>~=</math> |
<math> \frac{3(n+1) }{(5-n)} ~\biggl( \Theta^' \biggr)^2_{\tilde\xi} + \tilde\Theta^{n+1} \, , </math> |
Hence we can write,
|
<math>~\xi_e^2</math> |
<math>~=</math> |
<math>~\frac{4\pi }{(n+1) } \biggl[ \frac{3\mathcal{B}}{4\pi} \cdot \frac{1}{\tilde\mathfrak{f}_A} \biggr]^{(n-1)/(n+1)} \chi_\mathrm{eq}^{(3-n)/n} \, , </math> |
or,
|
<math>~\xi_e^2 \biggl[ \frac{3(n+1) }{(5-n)} ~\biggl( \Theta^' \biggr)^2_{\tilde\xi} + \tilde\Theta^{n+1} \biggr]^{(n-1)/(n+1)}</math> |
<math>~=</math> |
<math>~\frac{4\pi }{(n+1) } \biggl[ \frac{3\mathcal{B}}{4\pi} \biggr]^{(n-1)/(n+1)} \chi_\mathrm{eq}^{(3-n)/n} \, . </math> |
This last expression may be useful because the numerical value of the right-hand-side will be known once an extremum of a free-energy plot has been identified, while the function on the left-hand side can be evaluated separately, from knowledge of the internal structure of detailed force-balanced, isolated polytropes.
Strategy2
- Pick the desired polytropic index, <math>~n</math>, and a radial coordinate within the isolated polytropic model, <math>~\tilde\xi \leq \xi_1</math>, that will serve as the truncated edge of the embedded polytrope.
- Knowledge of the isolated polytrope's internal structure will give the value of the Lane-Emden function, <math>~\tilde\theta</math>, and its radial derivative, <math>~{\tilde\theta'}</math>, at this truncated edge of the structure.
- According to Horedt (1970) — see our accompanying discussion of detailed force-balanced models — the physical radius and external pressure that corresponds to this choice of the truncated edge is given by the expressions,
|
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} = r_a \biggl( \frac{R_\mathrm{Horedt}}{R_\mathrm{norm}} \biggr) </math> |
<math>~=~</math> |
<math> \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \biggl[ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{n-1} \biggr]^{1/(n-3)} \, , </math> |
|
<math> ~\frac{P_e}{P_\mathrm{norm}} = p_a \biggl( \frac{P_\mathrm{Horedt}}{P_\mathrm{norm}} \biggr) </math> |
<math>~=~</math> |
<math> \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2} \biggr]^{(n+1)/(n-3)} \, . </math> |
- Using the chosen value of <math>~\tilde\xi</math> and its associated function values, <math>~\tilde\theta</math> and <math>~\tilde\theta^'</math>, determine the values of the three relevant structural form factors via the following analytic relations:
|
<math>~\tilde\mathfrak{f}_M = \frac{\bar\rho}{\rho_c}</math> |
<math>~=</math> |
<math>~ \biggl[ - \frac{3 \tilde\theta^'}{\tilde\xi} \biggr] \, ,</math> |
|
<math>\tilde\mathfrak{f}_W </math> |
<math>~=</math> |
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\tilde\theta^'}{\tilde\xi} \biggr]^2 = \biggl( \frac{5}{5-n} \biggr) \tilde\mathfrak{f}_M^2 \, ,</math> |
|
<math>\tilde\mathfrak{f}_A = \frac{\bar{P}}{P_c}</math> |
<math>~=</math> |
<math> \frac{3(n+1) }{(5-n)} ~( \tilde\theta^')^2 + \tilde\theta^{n+1} \, . </math> |
- Using these values of the structural form factors, determine the values of the three free-energy coefficients (set <math>~M_\mathrm{limi}/M_\mathrm{tot} = 1</math> for the time being) via the expressions:
|
<math>~\mathcal{A}_\mathrm{mod} \equiv (5-n)\mathcal{A}</math> |
<math>~=</math> |
<math>\frac{(5-n)}{5} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} = \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \, ,</math> |
|
<math>~\mathcal{B}_\mathrm{mod} \equiv (5-n)\mathcal{B}</math> |
<math>~=</math> |
<math> \biggl( \frac{3}{4\pi} \biggr)^{1/n} \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{(n+1)/n} \cdot [(5-n)\tilde\mathfrak{f}_A] </math> |
|
|
<math>~=</math> |
<math> \frac{4\pi}{3} \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^{3(n+1)/n} \cdot [(5-n)\tilde\mathfrak{f}_A] </math> |
|
<math>~\mathcal{D}_\mathrm{mod} \equiv (5-n) \mathcal{D}</math> |
<math>~=</math> |
<math> \biggl( \frac{4\pi}{3} \biggr) (5-n) \frac{P_e}{P_\mathrm{norm}} \, . </math> |
- Plot the following free-energy function and see if the value of <math>~\chi</math> associated with the extremum is equal to the dimensionless equilibrium radius, <math>~R_\mathrm{eq}/R_\mathrm{norm}</math>, as predicted by Hoerdt's expression, above:
|
<math>~(5-n)\mathfrak{G}^*</math> |
<math>~=</math> |
<math>~-3\mathcal{A}_\mathrm{mod} \chi^{-1} -~ \frac{1}{(1-\gamma_g)} \mathcal{B}_\mathrm{mod} \chi^{3-3\gamma_g} +~ \mathcal{D}_\mathrm{mod}\chi^3</math> |
|
|
<math>~=</math> |
<math>~-3\mathcal{A}_\mathrm{mod} \chi^{-1} +n\mathcal{B}_\mathrm{mod} \chi^{-3/n} +~ \mathcal{D}_\mathrm{mod}\chi^3 \, .</math> |
- Virial equilbrium — that is, an extremum in the free energy function — occurs when <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>, that is, where,
|
<math>~\mathcal{B}_\mathrm{mod} \chi_\mathrm{eq}^{(n-3)/n} - \mathcal{D}_\mathrm{mod}\chi_\mathrm{eq}^4</math> |
<math>~=</math> |
<math>~\mathcal{A}_\mathrm{mod} \, .</math> |
Note that if the coefficient, <math>~\mathcal{B}</math>, is written in terms of the normalized central pressure, the statement of virial equilibrium becomes,
|
<math>~\mathcal{A}_\mathrm{mod} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{4\pi}{3}\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^{3(n+1)/n} \cdot [(5-n)\tilde\mathfrak{f}_A] \biggr] \chi_\mathrm{eq}^{(n-3)/n} - \frac{4\pi}{3} (5-n)\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^4</math> |
|
|
<math>~=</math> |
<math>~\frac{4\pi}{3}\chi_\mathrm{eq}^4 \biggl\{\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \cdot (5-n)\tilde\mathfrak{f}_A - (5-n)\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{4\pi}{3}\chi_\mathrm{eq}^4 \biggl\{\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \cdot \biggl[ 3(n+1) (\tilde\theta^')^2 + (5-n)\tilde\theta^{n+1} \biggr] - (5-n)\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \biggr\} \, . </math> |
But, in this situation, <math>~\tilde\theta^{n+1} = P_e/P_c</math>, so virial equilibrium implies,
|
<math>~\frac{3}{4\pi}\chi_\mathrm{eq}^{-4} \mathcal{A}_\mathrm{mod} </math> |
<math>~=</math> |
<math>~\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \cdot \biggl[ 3(n+1) (\tilde\theta^')^2 + (5-n)\frac{P_e}{P_c} \biggr] - (5-n)\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) </math> |
|
|
<math>~=</math> |
<math>~3(n+1) (\tilde\theta^')^2\biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) </math> |
|
<math>~\Rightarrow~~~\frac{P_c}{P_\mathrm{norm}} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2} </math> |
<math>~=</math> |
<math>~\biggl[ 4\pi(n+1) (\tilde\theta^')^2 \biggr]^{-1} </math> |
|
<math>~\Rightarrow~~~\frac{P_c R_\mathrm{eq}^4}{GM_\mathrm{limit}^2} </math> |
<math>~=</math> |
<math>~\frac{1}{4\pi(n+1) (\tilde\theta^')^2} \, . </math> |
Compare With Detailed Force Balanced Solution
In a separate discussion, we presented the detailed force-balanced model of an <math>~n=1</math> polytrope that is embedded in an external medium. We showed that, for an applied external pressure given by,
<math>\frac{P_e}{P_\mathrm{norm}} = \frac{\pi}{2} \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2 \, ,</math>
the associated equilibrium radius of the pressure-confined configuration is,
<math> R_\mathrm{eq} = \xi_e a_\mathrm{n=1} = \biggl[ \frac{K}{2\pi G} \biggr]^{1/2} \xi_e \, . </math>
Flipping this around, after we use a plot of the free-energy expression to identify the equilibrium radius, <math>~\chi_\mathrm{eq}</math>, the corresponding dimensionless radius as used in the Lane-Emden equation should be,
|
<math>~\xi_e</math> |
<math>~=</math> |
<math> \biggl[ \frac{2\pi G}{K} \biggr]^{1/2} R_\mathrm{norm} \cdot \chi_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>~(2\pi)^{1/2} \chi_\mathrm{eq} \, . </math> |
Keep in mind that, for an isolated <math>~n=1</math> polytrope, the (zero pressure) surface is identified by <math>~\xi_1 = \pi</math>. Hence we should expect free-energy extrema to occur at values of <math>~\chi_\mathrm{eq} \le \pi/2</math>.
Renormalization
Grunt Work
Returning to the dimensionless form of the virial expression and multiplying through by <math>~[-\chi_\mathrm{eq}/(3D)]</math>, we obtain,
<math> \chi_\mathrm{eq}^4 = \frac{B}{D} \chi_\mathrm{eq}^{4-3\gamma_g} - \frac{A}{D} \, , </math>
or, after plugging in definitions of the coefficients, <math>~A</math>, <math>~B</math>, and <math>~D</math>, and rewriting <math>~\chi_\mathrm{eq}</math> explicitly as <math>~R_\mathrm{eq}/R_\mathrm{norm}</math>,
|
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 </math> |
<math>~=</math> |
<math> \biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{4-3\gamma_g} - \frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \, .</math> |
This relation can be written in a more physically concise form, as follows. First, normalize <math>~P_e</math> to a new pressure scale — call it <math>~P_\mathrm{ad}</math> — and multiply through by <math>~(R_\mathrm{norm}/R_\mathrm{ad})^4</math> in order to normalizing <math>~R_\mathrm{eq}</math> to a new length scale,<math>~R_\mathrm{ad}</math>:
|
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{ad}} \biggr)^4 </math> |
<math>~=</math> |
<math> \biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{P_e}{P_\mathrm{ad}} \biggr)^{-1} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}} \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g}\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{ad}} \biggr)^{4-3\gamma_g} </math> |
|
|
|
<math> ~- \frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggl( \frac{P_e}{P_\mathrm{ad}} \biggr)^{-1} \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} \, , </math> |
or,
|
<math>~\chi_\mathrm{ad}^4 </math> |
<math>~=</math> |
<math> \biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}}\cdot \frac{\chi_\mathrm{ad}^{4-3\gamma_g} }{\Pi_\mathrm{ad}} - \frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \cdot \frac{1}{\Pi_\mathrm{ad}} \, ,</math> |
where,
|
<math>~\chi_\mathrm{ad}</math> |
<math>~\equiv</math> |
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{ad}} \, ,</math> |
|
<math>~\Pi_\mathrm{ad}</math> |
<math>~\equiv</math> |
<math>~\frac{P_\mathrm{e}}{P_\mathrm{ad}} \, .</math> |
By demanding that the leading coefficients of both terms on the right-hand-side of the expression are simultaneously unity — that is, by demanding that,
|
<math>~\biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}}</math> |
<math>~=</math> |
<math>~1 \, ,</math> |
and,
|
<math>~\frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} </math> |
<math>~=</math> |
<math>~1 \, ,</math> |
we obtain the expressions for <math>~R_\mathrm{ad}/R_\mathrm{norm}</math> and <math>~P_\mathrm{ad}/P_\mathrm{norm}</math> as shown in the following table.
|
Renormalization for Adiabatic (ad) Systems | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Using these new normalizations, we arrive at the desired, concise virial equilibrium relation, namely,
|
<math>~\Pi_\mathrm{ad} </math> |
<math>~=</math> |
<math>~\chi_\mathrm{ad}^{-3\gamma_g} - \chi_\mathrm{ad}^{-4} \, ,</math> |
or,
|
<math>~\chi_\mathrm{ad}^{4-3\gamma_g} - \Pi_\mathrm{ad} \chi_\mathrm{ad}^4</math> |
<math>~=</math> |
<math>~1 \, .</math> |
For the sake of completeness, we should develop expressions for both <math>~\chi_\mathrm{ad}</math> and <math>~\Pi_\mathrm{ad}</math> that are entirely in terms of the Lane-Emden function, <math>~\tilde\theta</math>, its derivative, <math>~\tilde\theta'</math>, and the associated dimensionless radial coordinate, <math>\tilde\xi</math>, at which the function and its derivative are to be evaluated. (Adopting a unified notation, we will set <math>~\gamma_g \rightarrow (n+1)/n</math>.)
|
<math>~\chi_\mathrm{ad} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{ad}}</math> |
<math>~=</math> |
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{Hoerdt}} \cdot \frac{R_\mathrm{Hoerdt}}{R_\mathrm{norm}} \cdot \frac{R_\mathrm{norm}}{R_\mathrm{ad}}</math> |
|
|
<math>~=</math> |
<math>~ r_a \cdot \biggl[ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} \biggr]^{1/(n-3)} \cdot \biggl[ 5^n \biggl( \frac{3}{4\pi} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{1-n} \frac{\tilde\mathfrak{f}_A^n}{\tilde\mathfrak{f}_W^n \cdot \tilde\mathfrak{f}_M^{1-n}} \biggr]^{1/(n-3)} </math> |
|
<math>~\Rightarrow~~~\chi_\mathrm{ad}^{n-3} </math> |
<math>~=</math> |
<math>~ 3 r_a^{n-3} \cdot \biggl[ \frac{5}{(n+1)} \cdot \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_W} \biggr]^n \tilde\mathfrak{f}_M^{n-1} \, . </math> |
Inserting the functional expressions for Hoerdt's <math>~r_a</math> and our structural form factors, <math>\tilde\mathfrak{f}_i</math>, gives,
|
<math>~\chi_\mathrm{ad}^{n-3}</math> |
<math>~=</math> |
<math>~ 3 \tilde\mathfrak{f}_A^n \biggl[ \tilde\xi^{n-3} (-\tilde\xi^2 \tilde\theta')^{1-n} \biggr] \biggl[ \frac{5}{(n+1)} \cdot \frac{(5-n)}{5\cdot 3^2} \biggl( - \frac{\tilde\xi}{\tilde\theta'} \biggr)^2\biggr]^n \biggl[- \frac{3 \tilde\theta'}{\tilde\xi} \biggr]^{n-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(5-n)}{3(n+1)} \cdot \frac{\tilde\mathfrak{f}_A}{(-\tilde\theta')^2}\biggr]^n </math> |
|
<math>~\Rightarrow ~~~~ \chi_\mathrm{ad}^{(n-3)/n}</math> |
<math>~=</math> |
<math>~ \frac{(5-n)}{3(n+1)} \cdot (-\tilde\theta')^{-2} \biggl[ \frac{3(n+1)}{(5-n)} (-\tilde\theta')^2 + \theta^{n+1} \biggr] </math> |
|
|
<math>~=</math> |
<math>~1 + \frac{(5-n)}{3(n+1)} \cdot \frac{\tilde\theta^{n+1}}{(-\tilde\theta')^2} \, . </math> |
And,
|
<math>~\Pi_\mathrm{ad} \equiv \frac{P_e}{P_\mathrm{ad}}</math> |
<math>~=</math> |
<math>~\frac{P_e}{P_\mathrm{Hoerdt}} \cdot \frac{P_\mathrm{Hoerdt}}{P_\mathrm{norm}} \cdot \frac{P_\mathrm{norm}}{P_\mathrm{ad}}</math> |
|
|
<math>~=</math> |
<math>~ p_a \cdot \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{(n+1)/(n-3)} \cdot \biggl[ \tilde\mathfrak{f}_A^{-4n} \cdot \biggl( \frac{4\pi}{3\cdot 5^3} \cdot \frac{\tilde\mathfrak{f}_W^3}{\tilde\mathfrak{f}_M^2} \biggr)^{(n+1)} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2(n+1)} \biggr]^{1/(n-3)} </math> |
|
<math>~\Rightarrow~~~\Pi_\mathrm{ad}^{n-3} </math> |
<math>~=</math> |
<math>~ p_a^{n-3}~ \tilde\mathfrak{f}_A^{-4n} \cdot \biggl[ \frac{(n+1)^3}{3\cdot 5^3} \biggl( \frac{\tilde\mathfrak{f}_W^3}{\tilde\mathfrak{f}_M^2} \biggr) \biggr]^{n+1} \, . </math> |
Inserting the functional expressions for Hoerdt's <math>~p_a</math> and our structural form factors, <math>\tilde\mathfrak{f}_i</math>, gives,
|
<math>~\Pi_\mathrm{ad}^{n-3} </math> |
<math>~=</math> |
<math>~ \tilde\mathfrak{f}_A^{-4n} ~[ \tilde\theta^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} ]^{n-3} \cdot \biggl[ \frac{(n+1)^3}{3\cdot 5^3}\biggr]^{n+1} \biggl[ \frac{3^2\cdot 5}{5-n} \biggl( \frac{\tilde\theta^'}{\tilde\xi} \biggr)^2 \biggr]^{3(n+1)} \bigg( - \frac{3\tilde\theta^'}{\tilde\xi} \biggr)^{-2(n+1)} </math> |
|
|
<math>~=</math> |
<math>~ \tilde\mathfrak{f}_A^{-4n} ~\biggl\{ \tilde\theta^{n-3}( -\tilde\xi^2 \tilde\theta' )^{2} \cdot \biggl[ \frac{(n+1)^3}{3\cdot 5^3}\biggr] \biggl[ \frac{3^2\cdot 5}{5-n} \biggl( \frac{\tilde\theta^'}{\tilde\xi} \biggr)^2 \biggr]^{3} \bigg( - \frac{3\tilde\theta^'}{\tilde\xi} \biggr)^{-2} \biggr\}^{n+1} </math> |
|
|
<math>~=</math> |
<math>~\tilde\theta^{(n+1)(n-3)} \tilde\mathfrak{f}_A^{-4n} ~\biggl[ \frac{3(n+1)}{(5-n)} ( -\tilde\theta' )^{2} \biggr]^{3(n+1)} </math> |
|
|
<math>~=</math> |
<math>~\tilde\theta^{(n+1)(n-3)} \biggl[ \frac{3(n+1) }{(5-n)} ~( \tilde\theta^' )^2 + \tilde\theta^{n+1} \biggr]^{-4n} ~\biggl[ \frac{3(n+1)}{(5-n)} ( \tilde\theta' )^{2} \biggr]^{3(n+1)} \, . </math> |
(Not a particularly simple or transparent expression!)
Summary
Defining,
|
<math>~a_\mathrm{ad}</math> |
<math>~\equiv</math> |
<math>~\frac{3(n+1) }{(5-n)} ~(\tilde\theta^' )^2 \, ,</math> and, |
|
<math>~b_\mathrm{ad}</math> |
<math>~\equiv</math> |
<math>~\tilde\theta^{n+1} \, ,</math> |
the expressions for the dimensionless equilibrium radius and the dimensionless external pressure may be written as, respectively,
|
<math>~\chi_\mathrm{ad}</math> |
<math>~=</math> |
<math>~ \biggl[ 1 + \frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggr]^{n/(n-3)} \, , </math> and, |
|
<math>~\Pi_\mathrm{ad} </math> |
<math>~=</math> |
<math>~ b_\mathrm{ad} \biggl[ \frac{a_\mathrm{ad}^{3(n+1)} }{( a_\mathrm{ad} + b_\mathrm{ad} )^{4n} } \biggr]^{1/(n-3)} = \frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggl[ 1 + \frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggr]^{-4n/(n-3)} \, . </math> |
Using these expressions, it is easy to demonstrate that the virial equilibrium relation is satisfied, namely,
|
<math>~\Pi_\mathrm{ad} </math> |
<math>~=</math> |
<math>~\chi_\mathrm{ad}^{-3(n+1)/n} - \chi_\mathrm{ad}^{-4} \, .</math> |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
P-V Diagram for Unity Form Factors
Writing the coefficient, <math>B</math>, in terms of the average sound speed and setting the radial scale factor equal to the equilibrium radius of an isolated adiabatic sphere, that is, setting,
<math> R_0 = \frac{GM}{5\bar{c_s}^2} \, , </math>
the equation governing the radii of adiabatic equilibrium states becomes,
<math> \chi^4 - \frac{1}{\Pi_a} \chi^{(4-3\gamma_g)} + \frac{1}{\Pi_a} = 0 \, , </math>
where,
<math> \Pi_a \equiv \frac{4\pi P_e G^3 M^2}{3\cdot 5^3 \bar{c_s}^8} \, . </math>
As in the isothermal case, for a given choice of configuration mass and sound speed, this parameter, <math>\Pi_a</math>, can be viewed as a dimensionless external pressure. Alternatively, for a given choice of <math>P_e</math> and <math>\bar{c_s}</math>, <math>\Pi_a^{1/2}</math> can represent a dimensionless mass; or, for a given choice of <math>M</math> and <math>P_e</math>, <math>\Pi_a^{-1/8}</math> can represent a dimensionless sound speed. Here we will view it as a dimensionless external pressure.
Unlike the isothermal case, for an arbitrary value of the adiabatic exponent, <math>\gamma_g</math>, it isn't possible to invert this equation to obtain an analytic expression for <math>\chi</math> as a function of <math>\Pi_a</math>. But we can straightforwardly solve for <math>\Pi_a</math> as a function of <math>\chi</math>. The solution is,
<math> \Pi_a = \frac{\chi^{(4- 3\gamma_g)} - 1}{\chi^4} \, . </math>
For physically relevant solutions, both <math>\chi</math> and <math>\Pi_a</math> must be nonnegative. Hence, as is illustrated by the curves in Figure 4, the physically allowable range of equilibrium radii is,
<math> 1 \le \chi \le \infty \, ~~~~~\mathrm{for}~ \gamma_g < 4/3 \, ; </math>
<math> 0 < \chi \le 1 \, ~~~~~~\mathrm{for}~ \gamma_g > 4/3 \, . </math>
|
Figure 4: Equilibrium Adiabatic P-V Diagram |
|
|
The curves trace out the function, <math> \Pi_a = (\chi^{4-3\gamma_g} - 1)/\chi^4 \, , </math> for six different values of <math>\gamma_g</math> (<math>2, ~5/3, ~7/5, ~6/5, ~1, ~2/3</math>, as labeled) and show the dimensionless external pressure, <math>\Pi_a</math>, that is required to construct a nonrotating, self-gravitating, uniform density, adiabatic sphere with an equilibrium radius <math>\chi</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative. The solid red curve, drawn for the case <math>\gamma_g = 1</math>, is identical to the solid black (isothermal) curve displayed above in Figure 1. |
|
Each of the <math>\Pi_a(\chi)</math> curves drawn in Figure 4 exhibits an extremum. In each case this extremum occurs at a configuration radius, <math>\chi_\mathrm{extreme}</math>, given by,
<math> \frac{\partial\Pi_a}{\partial\chi} = 0 \, , </math>
that is, where,
<math> 4 - 3\gamma_g \chi^{4-3\gamma_g} = 0 ~~~~\Rightarrow ~~~~~ \chi_\mathrm{extreme} = \biggl[ \frac{4}{3\gamma_g} \biggr]^{1/(4-3\gamma_g)} \, . </math>
For each value of <math>\gamma_g</math>, the corresponding dimensionless pressure is,
<math> \Pi_a \biggr|_\mathrm{extreme} = \biggl(\frac{4}{3\gamma} - 1 \biggr) \biggl[ \frac{3\gamma_g}{4} \biggr]^{4/(4-3\gamma_g)} \, . </math>
Note, first, that for <math>\gamma_g > 4/3</math>, an equilibrium configuration with a positive radius can be constructed for all physically realistic — that is, for all positive — values of <math>\Pi_a</math>. Also, consistent with the behavior of the curves shown in Figure 4, the extremum arises in the regime of physically relevant — i.e., positive — pressures only for values of <math>\gamma_g < 4/3</math>; and in each case it represents a maximum limiting pressure.
Maximum Mass
<math>n=5</math> Polytropic
When <math>\gamma_a = 6/5</math> — which corresponds to an <math>n=5</math> polytropic configuration — we obtain,
<math> \Pi_\mathrm{max} = \Pi_a\biggr|_\mathrm{extreme}^{(\gamma_g = 6/5)} = \biggl( \frac{3^{18}}{2^{10}\cdot 5^{10}} \biggr) \, , </math>
which corresponds to a maximum mass for pressure-bounded <math>n=5</math> polytropic configurations of,
<math>M_\mathrm{max} = \Pi_\mathrm{max}^{1/2} \biggl(\frac{3\cdot 5^3}{2^2\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} = \biggl(\frac{3^{19}}{2^{12}\cdot 5^{7}\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} \, .</math>
This result can be compared to other determinations of the Bonnor-Ebert mass limit.
More Precise Form Factors
Here we attempt to determine proper expressions for several form factors such that the equilibrium configurations determined from virial analysis will precisely match the pressure-truncated polytropic configurations that have been determined from detailed force-balanced models that have been derived and published separately by Horedt (1970), by Whitworth (1981) and by Stahler (1983). It seems simplest to begin with the free-energy expressions that we have already generalized in the context of bipolytropic configurations, properly modified to embed the "core" in an external medium of pressure, <math>~P_e</math>, rather then inside an envelope that has a different polytropic index. Specifically,
|
<math>~\mathfrak{G}^* \equiv \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr)_\mathrm{core} + \biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core} + \biggl( \frac{P_e V}{E_\mathrm{norm}} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ -3\mathcal{A} \chi^{-1} - \frac{\mathcal{B}_\mathrm{core}}{(1-\gamma_c)} \chi^{3-3\gamma_c} + \mathcal{D} \chi^3 \, , </math> |
where,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{\nu}{q^3} \biggr) \int_0^{q} \biggl[\frac{M_r(x)}{M_\mathrm{tot}} \biggr]_\mathrm{core} \biggl[ \frac{\rho(x)}{\bar\rho} \biggr]_\mathrm{core} x dx \, , </math> |
|
<math>~\mathcal{B}_\mathrm{core}</math> |
<math>~\equiv</math> |
<math> \frac{4\pi}{3} \biggl[ \frac{P_{ic} \chi^{3\gamma_c}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \int_0^q 3\biggl[\frac{1 - p_c(x)}{1-p_c(q)} \biggr] x^2 dx = \frac{4\pi}{3} \biggl[ \frac{P_e \chi^{3\gamma_c}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \biggl[ q^3 s_\mathrm{core} \biggr] \, , </math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math> \chi^{-3} \biggl[ \frac{P_e V}{P_\mathrm{norm} R_\mathrm{norm}^3} \biggr] = \biggl(\frac{P_e}{P_\mathrm{norm}} \biggr) \int_0^q 4\pi x^2 dx = \frac{4\pi q^3}{3} \biggl(\frac{P_e}{P_\mathrm{norm}} \biggr) \, . </math> |
Virial equilibrium occurs where <math>~\partial\mathfrak{G}/\partial \chi = 0</math>, that is, when,
|
<math>~\mathcal{A} \chi_\mathrm{eq}^{-1}</math> |
<math>~=</math> |
<math>~\mathcal{B} \chi_\mathrm{eq}^{3-3\gamma_c} - \mathcal{D} \chi_\mathrm{eq}^{3} \, .</math> |
n = 5 Polytropic
From our analysis of the free energy of <math>~(n_c, n_e) = (5, 0)</math> bipolytropes, we deduce that the coefficient, <math>~\mathcal{A}</math>, that quantifies the gravitational potential energy of a pressure-truncated <math>~n = 5</math> polytrope is,
|
<math>~\mathcal{A} = - \frac{\chi}{3} \biggl( \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr)_\mathrm{core} </math> |
<math>~=</math> |
<math> \chi_\mathrm{eq} \biggl( \frac{3^6}{2^5\pi} \biggr)^{1/2} \biggl[ a_\xi^{1/2} q(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) (a_\xi q^2 +1)^{-3} + \tan^{-1}(a_\xi^{1/2} q) \biggr] \, ; </math> |
the coefficient, <math>~\mathcal{B}_\mathrm{core}</math>, that quantifies the thermal energy content of a pressure-truncated <math>~n = 5</math> polytrope is,
|
<math>~\mathcal{B} = (\gamma_c-1) \chi^{3\gamma_c-3}\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> |
<math>~=</math> |
<math> \chi_\mathrm{eq}^{3/5} \biggl( \frac{3^6}{2^5\pi} \biggr)^{1/2} \biggl[ \tan^{-1}[a_\xi^{1/2}q] - a_\xi^{1/2}q ~\frac{(1 - a_\xi q^2)}{(1 + a_\xi q^2)^2} \biggr] \, ; </math> |
and the coefficient, <math>~\mathcal{D}</math> — which can be obtained by setting <math>~P_{ic} \rightarrow P_e</math> in expressions drawn from out analysis of the thermal energy content of an <math>~(5, 0)</math>bipolytrope — is,
|
<math>\mathcal{D} = \biggl(\frac{2q^3}{3 \chi_\mathrm{eq}^3} \biggr) \biggl[ \frac{2\pi P_{ic} \chi_\mathrm{eq}^3}{P_\mathrm{norm}} \biggr] </math> |
<math>~=</math> |
<math> \chi_\mathrm{eq}^{-3} \biggl( \frac{2\cdot 3^4}{\pi} \biggr)^{1/2} \biggl(1 + a_\xi q^2 \biggr)^{-3} a_\xi^{3/2}q^3 \, . </math> |
Hence, virial equilibrium occurs when,
|
<math>~\mathcal{A} \chi_\mathrm{eq}^{-1}</math> |
<math>~=</math> |
<math>~\mathcal{B} \chi_\mathrm{eq}^{-3/5} - \mathcal{D} \chi_\mathrm{eq}^{3} \, ,</math> |
that is, when,
|
<math>~ \biggl( \frac{3^6}{2^5\pi} \biggr)^{1/2} \biggl[ a_\xi^{1/2} q(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) (a_\xi q^2 +1)^{-3} + \tan^{-1}(a_\xi^{1/2} q)\biggr] </math> |
<math>~=</math> |
<math>~ \biggl( \frac{3^6}{2^5\pi} \biggr)^{1/2} \biggl[ \tan^{-1}[a_\xi^{1/2}q] - a_\xi^{1/2}q ~\frac{(1 - a_\xi q^2)}{(1 + a_\xi q^2)^2} \biggr] </math> |
|
|
|
<math>~ - \biggl( \frac{2\cdot 3^4}{\pi} \biggr)^{1/2} \biggl(1 + a_\xi q^2 \biggr)^{-3} a_\xi^{3/2}q^3 \, . </math> |
|
<math>~\Rightarrow~~~~ \biggl[ a_\xi^{1/2} q(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) (a_\xi q^2 +1)^{-3} + \tan^{-1}(a_\xi^{1/2} q)\biggr] </math> |
<math>~=</math> |
<math>~ \biggl[ \tan^{-1}[a_\xi^{1/2}q] - a_\xi^{1/2}q ~\frac{(1 - a_\xi q^2)}{(1 + a_\xi q^2)^2} \biggr] - \biggl( \frac{2^3}{3} \biggr) \biggl(1 + a_\xi q^2 \biggr)^{-3} a_\xi^{3/2}q^3</math> |
|
<math>~\Rightarrow~~~~ a_\xi^{1/2} q(a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) </math> |
<math>~=</math> |
<math>~ - a_\xi^{1/2}q ~(1 - a_\xi q^2)(1 + a_\xi q^2)
- \biggl( \frac{2^3}{3} \biggr) a_\xi^{3/2}q^3</math> |
|
<math>~\Rightarrow~~~~ (a_\xi^2 q^4 - \frac{8}{3}a_\xi q^2 - 1) </math> |
<math>~=</math> |
<math>~ - (1 - a_\xi^2 q^4) - \biggl( \frac{2^3}{3} \biggr) a_\xi q^2 </math> |
|
<math>~\Rightarrow~~~~ 0 </math> |
<math>~=</math> |
<math>~ 0 \, . </math> |
So this will always be true!
The detailed force-balanced analysis of <math>~n=5</math> polytropes shows that the pair of equations defining the equilibrium (truncated) radius for a specified external pressure are,
<math> R_\mathrm{eq} = \biggl[ \frac{\pi M^4 G^5}{2^3 \cdot 3^7 K^5} \biggr]^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \, , </math>
<math>P_e= \biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 M^{6} G^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} </math> .
Applying our chosen normalizations, this pair of defining equations becomes,
|
<math>~\chi_\mathrm{eq} = \frac{R_\mathrm{eq}}{R_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{\pi M^4 G^5}{2^3 \cdot 3^7 K^5} \biggr]^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \cdot \biggl[\frac{K^5}{G^5 M_\mathrm{tot}^4} \biggr]^{1/2} = \biggl( \frac{\pi}{2^3 \cdot 3} \biggr)^{1/2} \xi_e^{-5} \biggl( 1+ \frac{1}{3}\xi_e^2 \biggr)^3 \, , </math> |
|
<math>~\frac{P_e}{P_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~\biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 M^{6} G^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} \cdot \biggl[\frac{G^9 M_\mathrm{tot}^6}{K^{10}} \biggr] = \biggr( \frac{2^3\cdot 3^{3} }{\pi^3} \biggr) \xi_e^{18} \biggl(1 + \frac{1}{3}\xi_e^2 \biggr)^{-12} \, . </math> |
Relationship to Detailed Force Balance Solution
Let's plug these form-factors into our expressions for the dimensionless equilibrium radius, <math>~\chi_\mathrm{ad}</math>, and dimensionless surface pressure, <math>~\Pi_\mathrm{ad}</math>, that have been derived from the identification of extrema in the free-energy function and see how they compare to the dimensionless radius, <math>~r_a \equiv R_\mathrm{eq}/R_\mathrm{Hoerdt}</math>, and dimensionless pressure, <math>~p_a \equiv P_e/P_\mathrm{Hoerdt}</math>, given by Horedt's (1970) detailed force-balance models. Note that expressions for <math>~r_a</math> and <math>~p_a</math> are given in our accompanying discussion of embedded polytropic spheres and that the conversion from Hoerdt's scaling parameters to our normalization parameters, <math>~R_\mathrm{Hoerdt}/R_\mathrm{norm}</math> and <math>~P_\mathrm{Hoerdt}/P_\mathrm{norm}</math>, can be found in our introductory discussion of the virial equilibrium of spherical configurations.
|
<math>~\chi_\mathrm{ad} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{ad}}</math> |
<math>~=</math> |
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{Hoerdt}} \biggl( \frac{R_\mathrm{Hoerdt}}{R_\mathrm{norm}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)</math> |
|
|
<math>~=</math> |
<math>~r_a \biggl[ \biggl(\frac{\gamma - 1}{\gamma}\biggr) (4\pi)^{\gamma-1}\biggr]^{1/(4-3\gamma)} \biggl[ 5 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_W \mathfrak{f}_M^{\gamma_g-2}} \biggr]^{1/(4-3\gamma_g)} </math> |
|
|
<math>~=</math> |
<math>~r_a \biggl[ 5 \cdot 3^{\gamma-1} \biggl(\frac{\gamma - 1}{\gamma}\biggr) \frac{\mathfrak{f}_A \mathfrak{f}_M^{2-\gamma_g}}{\mathfrak{f}_W } \biggr]^{1/(4-3\gamma_g)} </math> |
|
|
<math>~=</math> |
<math> r_a \biggl[ \frac{5 \cdot 3^{1/n} }{n+1} \cdot \frac{\mathfrak{f}_A \mathfrak{f}_M^{(n-1)/n}}{\mathfrak{f}_W } \biggr]^{n/(n-3)} = r_a \biggl[ 3 \mathfrak{f}_M^{n-1} \biggl( \frac{5 }{n+1} \cdot \frac{\mathfrak{f}_A }{\mathfrak{f}_W }\biggr)^n \biggr]^{1/(n-3)} </math> |
|
<math>~\Pi_\mathrm{ad} \equiv \frac{P_\mathrm{e}}{P_\mathrm{ad}}</math> |
<math>~=</math> |
<math>~\frac{P_\mathrm{e}}{P_\mathrm{Hoerdt}} \biggl( \frac{P_\mathrm{Hoerdt}}{P_\mathrm{norm}} \biggr) \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr)</math> |
|
|
<math>~=</math> |
<math>~p_a \biggl[ \biggl( \frac{\gamma}{\gamma-1}\biggr)^{3\gamma} (4\pi)^{-\gamma} \biggr]^{1/(4-3\gamma)} \biggl[ \mathfrak{f}_A^{-4} \biggl( \frac{4\pi}{3\cdot 5^3} \cdot \frac{\mathfrak{f}_W^3}{\mathfrak{f}_M^2} \biggr)^{\gamma_g} \biggr]^{1/(4-3\gamma_g)} </math> |
|
|
<math>~=</math> |
<math>~p_a \mathfrak{f}_A^{-4/(4-3\gamma)} \biggl[ \biggl( \frac{\gamma}{\gamma-1}\biggr)^{3} \biggl( \frac{1}{3\cdot 5^3} \cdot \frac{\mathfrak{f}_W^3}{\mathfrak{f}_M^2} \biggr)\biggr]^{\gamma/(4-3\gamma)} </math> |
|
|
<math>~=</math> |
<math> ~p_a \mathfrak{f}_A^{-4n/(n-3)} \biggl[ \frac{(n+1)^3}{3\cdot 5^3} \cdot \frac{\mathfrak{f}_W^3}{\mathfrak{f}_M^2} \biggr]^{(n+1)/(n-3)} </math> |
Now we insert the form-factor expressions from above, to obtain,
|
<math>~\chi_\mathrm{ad} </math> |
<math>~=</math> |
<math> r_a \biggl[ 3 \biggl( \frac{5 }{n+1} \biggr)^n \biggr]^{1/(n-3)} \biggl[ \frac{\mathfrak{f}_A^n \mathfrak{f}_M^{n-1} }{\mathfrak{f}_W^n } \biggr]^{1/(n-3)} </math> |
|
|
<math>~=</math> |
<math> r_a \biggl[ 3 \biggl( \frac{5 }{n+1} \biggr)^n \biggr]^{1/(n-3)} \biggl\{ \biggl[ \frac{3(n+1) }{(5-n)} ~( \Theta^' )^2 \biggr]^n \biggl[ \frac{3^2\cdot 5}{5-n} \biggl( \frac{\Theta^'}{\xi} \biggr)^2 \biggr]^{-n} \biggl[ - \frac{3\Theta^'}{\xi} \biggr]^{n-1} \biggr\}^{1/(n-3)}_{\xi_1} </math> |
|
|
<math>~=</math> |
<math> r_a \biggl\{ 3^n \biggl( \frac{5 }{n+1} \biggr)^n \biggl[ \frac{3(n+1) }{(5-n)} \biggr]^n \biggl[ \frac{5-n}{3^2\cdot 5} \biggr]^{n} \biggr\}^{1/(n-3)} \biggl\{ \xi^{2n} \biggl[ - \frac{\Theta^'}{\xi} \biggr]^{n-1} \biggr\}^{1/(n-3)}_{\xi_1} </math> |
|
|
<math>~=</math> |
<math> r_a \biggl[ \xi^{n+1} ( - \Theta^' )^{n-1} \biggr]^{1/(n-3)}_{\xi_1} </math> |
|
<math>~\Pi_\mathrm{ad} </math> |
<math>~=</math> |
<math> ~p_a \mathfrak{f}_A^{-4n/(n-3)} \biggl[ \frac{(n+1)^3}{3\cdot 5^3} \cdot \frac{\mathfrak{f}_W^3}{\mathfrak{f}_M^2} \biggr]^{(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~p_a \biggl[ \frac{3(n+1) }{(5-n)} ~( \Theta^' )^2 \biggr]_{\tilde\xi}^{-4n/(n-3)} \biggl\{ \frac{(n+1)^3}{3\cdot 5^3} \cdot \biggl[\frac{3^2\cdot 5}{5-n} \biggl( \frac{\Theta^'}{\xi} \biggr)^2\biggr]^3 \biggl[ - \frac{3\Theta^'}{\xi} \biggr]^{-2} \biggr\}^{(n+1)/(n-3)}_{\xi_1} </math> |
|
|
<math>~=</math> |
<math> ~p_a \biggl\{ \biggl[ \frac{5-n}{3(n+1)} \biggr]^{4n} \biggl[ \frac{(n+1)^3 \cdot 3^6 \cdot 5^3}{3^3 \cdot 5^3 (5-n)^3} \biggr]^{(n+1)} \biggr\}^{1/(n-3)} \biggl[ ( \Theta^' )^{-8n} \biggl( \frac{\Theta^'}{\xi} \biggr)^{4(n+1)} \biggr]^{1/(n-3)}_{\xi_1} </math> |
|
|
<math>~=</math> |
<math> ~p_a \biggl[ \frac{5-n}{3(n+1)} \biggr] \biggl[\xi^{n+1} ( \Theta^' )^{n-1} \biggr]^{-4/(n-3)}_{\xi_1} </math> |
Notice that the bracketed term that is to be evaluated at <math>~\xi_1</math> is identical in both expressions. After renormalization, as drived above, the statement of virial equilibrium for embedded polytropes is,
|
<math>~\chi_\mathrm{ad}^4</math> |
<math>~=</math> |
<math>~\frac{1}{\Pi_\mathrm{ad}} \biggl[ \chi_\mathrm{ad}^{4-3\gamma_g} - 1 \biggr] \, ,</math> |
or, setting <math>~\gamma_g = (n+1)/n</math>,
|
<math>~\Pi_\mathrm{ad} \chi_\mathrm{ad}^4</math> |
<math>~=</math> |
<math>~\chi_\mathrm{ad}^{(n-3)/n} - 1 \, .</math> |
This relation can now be written in terms of Horedt's (1970) dimensionless radius and pressure.
|
<math> ~p_a \biggl[ \frac{5-n}{3(n+1)} \biggr] \biggl[\xi^{n+1} ( \Theta^' )^{n-1} \biggr]^{-4/(n-3)}_{\xi_1} \cdot r_a^4 \biggl[ \xi^{n+1} ( - \Theta^' )^{n-1} \biggr]^{4/(n-3)}_{\xi_1} </math> |
<math>~=</math> |
<math>~ r_a^{(n-3)/n} \biggl[ \xi^{n+1} ( - \Theta^' )^{n-1} \biggr]^{1/n}_{\xi_1} - 1</math> |
|
<math> \Rightarrow ~~~~ p_a r_a^4 \biggl[ \frac{5-n}{3(n+1)} \biggr] </math> |
<math>~=</math> |
<math>~ r_a^{(n-3)/n} \biggl[ \xi^{n+1} ( - \Theta^' )^{n-1} \biggr]^{1/n}_{\xi_1} - 1 \, ,</math> |
where, from our separate summary of Hoerdt's presentation,
|
<math> ~r_a </math> |
<math>~=~</math> |
<math> \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} = \biggl[ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} \biggr]^{-1/(n-3)}\, , </math> |
|
<math> ~p_a </math> |
<math>~=~</math> |
<math> \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \, . </math> |
Hence, the virial relation becomes,
|
<math> ~1 </math> |
<math>~=</math> |
<math>~ \biggl\{ \frac{ [ \xi^{n+1} ( - \Theta^' )^{n-1} ]_{\xi_1} }{ [ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} ] } \biggr\}^{1/n}
- \biggl[ \frac{5-n}{3(n+1)} \biggr] \tilde\theta_n^{n+1} \biggl\{ \frac{( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)}}{ [ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} ]^{4/(n-3)} } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{ \xi_1^{n+1} ( - \Theta^' )^{n-1}_{\xi_1} }{ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} } \biggr]^{1/n}
- \biggl[ \frac{5-n}{3(n+1)} \biggr] \tilde\theta_n^{n+1} \biggl\{ \frac{ \tilde\xi^{4n+4} ( -\tilde\theta' )^{2n+2}}{ \tilde\xi^{4n+4} (-\tilde\theta^')^{4n-4} } \biggr\}^{1/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{ \xi_1^{n+1} ( - \Theta^' )^{n-1}_{\xi_1} }{ \tilde\xi^{n+1} (-\tilde\theta^')^{n-1} } \biggr]^{1/n}
- \biggl[ \frac{5-n}{3(n+1)} \biggr] \frac{ \tilde\theta_n^{n+1} }{ ( -\tilde\theta' )^{2} } \, .</math> |
This needs to be checked, perhaps with specific applications to the cases <math>~n=1</math> and <math>~n=5</math>.
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |