User:Tohline/Appendix/Ramblings/BordeauxSequences
Université de Bordeaux (Part 2)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Exterior Gravitational Potential of Toroids
J. -M. Huré, B. Basillais, V. Karas, A. Trova, & O. Semerák (2020), MNRAS, 494, 5825-5838 have published a paper titled, The Exterior Gravitational Potential of Toroids. Here we examine how their work relates to the published work by C.-Y. Wong (1973, Annals of Physics, 77, 279), which we have separately discussed in detail.
We discuss this topic in a separate, accompanying chapter.
Spheroid-Ring Systems
Through a research collaboration at the Université de Bordeaux, B. Basillais & J. -M. Huré (2019), MNRAS, 487, 4504-4509 have published a paper titled, Rigidly Rotating, Incompressible Spheroid-Ring Systems: New Bifurcations, Critical Rotations, and Degenerate States.
Key References
Here are some relevant publications:
- Hachisu (1986a, ApJS, 61, 479): A Versatile Method for Obtaining Structures of Rapidly Rotating Stars
- Fujisawa & Eriguchi (2014, MNRAS, 438, L61): Prolate stars due to meridional flows
- Huré, Hersant & Nasello (2018, MNRAS, 475, 63): The equilibrium of overpressurized polytropes
- & Eriguchi (1984, Ap&SS, 99, 71): Fission Sequence and Equilibrium Models of [Rigidly] Rotating Polytropes
- Hachisu, Eriguchi & Nomoto (1986b, ApJ, 311, 214): Fate of merging double white dwarfs. II - Numerical method
- Nishida, Eriguchi & Lanza (1992, ApJ, 401, 618): General Relativistic Structure of Star-Toroid Systems
- Woodward, Sankaran & Tohline (1992 ApJ, 394, 248): Tidal Disruption of a Star by a Massive Disk (The Axisymmetric Roche Problem)
Especially,
- Eriguchi & Hachisu (1983, Prog. Theor. Phys., 69, 1131): Two Kinds of Axially Symmetric Equilibrium Sequences of Self-Gravitating and Rotating Incompressible Fluids: Two-Ring Sequence and Core-Ring Sequence
- Ansorg, Kleinwächter & Meinel (2003, MNRAS, 339, 515): Uniformly rotating axisymmetric fluid configurations bifurcating from highly flattened Maclaurin spheroids
- Hachisu, Eriguchi & Nomoto (1986a, ApJ, 308, 161): Fate of Merging Double White Dwarfs
Key Figures
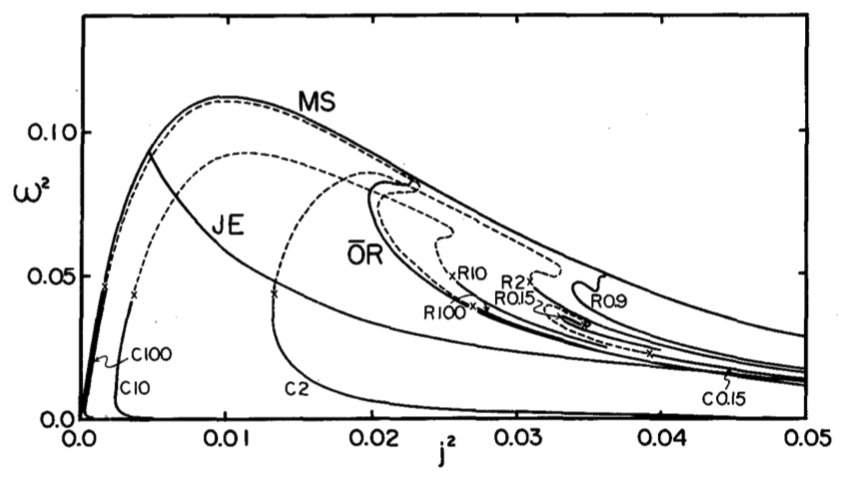
Eriguchi & Hachisu (1983)
|
Fig. 3 extracted without modification from p. 1134 of Eriguchi & Hachisu (1983)
"Two Kinds of Axially Symmetric Equilibrium Sequences of Self-Gravitating and Rotating Incompressible Fluids: Two-Ring Sequence and Core-Ring Sequence" Progress of Theoretical Physics, vol. 69, pp. 1131-1136 © Progress of Theoretical Physics |
|
CAPTION: The angular momentum-angular velocity relations. Solid curves represent uniformly rotating equilibrium sequences.
The number and letter R or C attached to a curve denote mass ratio and two-ring or core-ring sequence, respectively. If differential rotation is allowed, the equilibrium sequences may continue to exist as shown by the dashed curves. |
AKM (2003)
|
Fig. 2 extracted without modification from p. 517 of Ansorg, Kleinwächter & Meinel (2003)
"Uniformly rotating axisymmetric fluid configurations bifurcating from highly flattened Maclaurin spheroids"
MNRAS, vol. 339, pp. 515-523 © Royal Astronomical Society |
|
CAPTION: The angular momentum-angular velocity relations. Solid curves represent uniformly rotating equilibrium sequences.
The number and letter R or C attached to a curve denote mass ratio and two-ring or core-ring sequence, respectively. If differential rotation is allowed, the equilibrium sequences may continue to exist as shown by the dashed curves. |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |